Производная сложной функции. Полная производная

Пусть в области 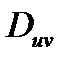задана функция двух переменных: у которой переменные u и v в свою очередь являются функциями переменных x и y:

заданными в области .

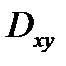Тогда z является сложной функцией независимых переменных x и y с промежуточными переменными u и v:

Рассмотрим задачу нахождения частных производных этой сложной функции. Пусть точка 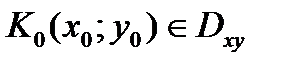, и функции j и y, переводят ее в точку :

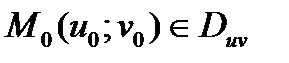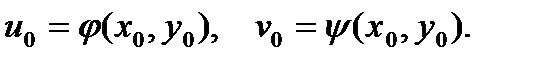
Теорема. Пусть выполняются три условия:

1.В окрестности точки существуют частные производные непрерывные в самой точке .

2. В точке 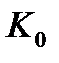существуют частные производные

3. Функции 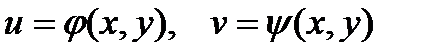непрерывны в точке .

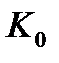Тогда в точке 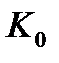существуют частные производные сложной функции , и для них справедливы формулы:

или в другой записи: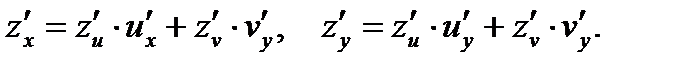

Так как общие формулы производных сложных функций имеют громоздкий вид, рассмотрим общий принцип нахождения этих производных на примере.

Пример 1

Дана сложная функция 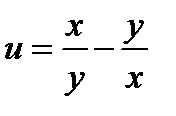, где . Найти её производную и записать полный дифференциал 1-го порядка.

Решение:

1) Дана функция, зависящая от x и y, которые в свою очередь являются функциями одной переменной:

2) Требуется найти не частные производные. Так как функция 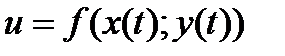фактически зависит только от одной переменной, то под словом «производная» подразумевается полная производная

Конечно можно выполнить прямую подстановку и взять производную функции одной переменной, т.е.

Подставить в функцию :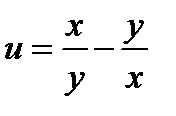

И, соответственно, полный дифференциал:

Это решение математически корректно, но выполненная подстановка дает лишь частную информацию о функции, к тому же, формулировка задачи предполагает использование универсальной формулы:

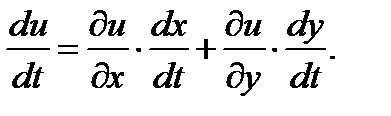
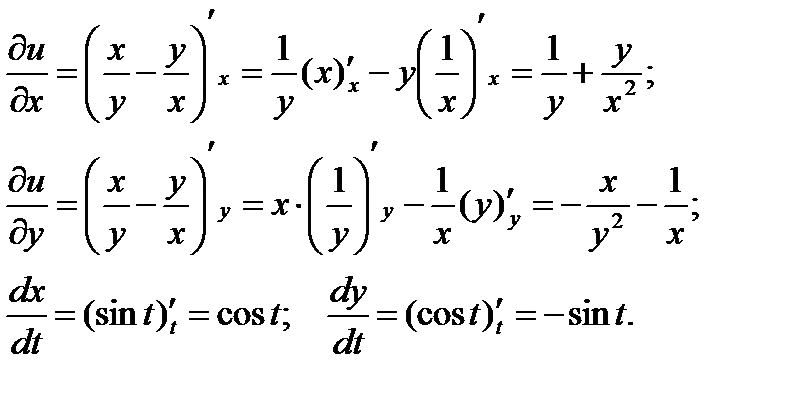
Подставим найденные производные в нашу формулу:

Когда функция изначально предложена в замысловатом виде, то логично оставить в таком же виде и результаты:

4.3.7 Инвариантность формы первого дифференциала.

В том случае, когда x и y являются независимыми аргументами функции 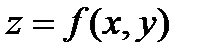, была установлена следующая форма ее дифференциала:

В случае, если z зависим от x и y сложным образом, т. е. через посредство некоторых функций, 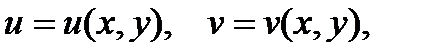т.е. 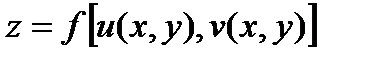, то частные производные будут выражаться по формулам:

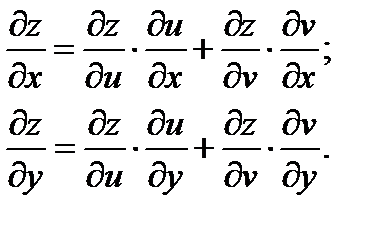
При этом оказывается, что форма дифференциала не изменится, если его выразить только через u и v и их дифференциалы, т. к. имеет место теорема об инвариантности формы первого дифференциала функции многих переменных.

Теорема. Дифференциал функции 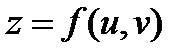сохраняет один и тот же вид независимо от того, являются ли ее аргументы независимыми переменными или функциями от независимых переменных.