2017-10-31
4986
Пусть функция 
определена в некоторой окрестности точки 
Придадим переменной x приращение 
оставляя при этом значение переменной y без изменения так, чтобы точка 
принадлежала этой окрестности.
Определение. Величину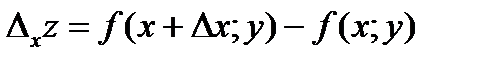 
называют частным приращением функции по переменной x.
Аналогично вводится частное приращение 
этой функции по переменной y: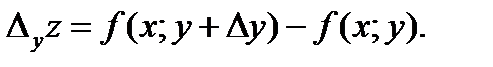 
Полное приращение 
функции определяется равенством 
Если существует предел 
то он называется частной производной функции в точке по переменной x и обозначается одним из следующих символов:
Аналогично частная производная функции по переменной y определяется как предел: 
Она обозначается как 
Согласно с определением, при нахождении частной производной 
находят обыкновенную производную функции одной переменной x считая переменную y постоянной, а при нахождении производной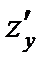 
постоянной считается переменная x.
Следовательно, частные производные находятся по формулам и правилам дифференцирования функции одной переменной.
Частная производная характеризует скорость изменения функции в направлении оси Ox, 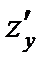– в направлении оси Oy.
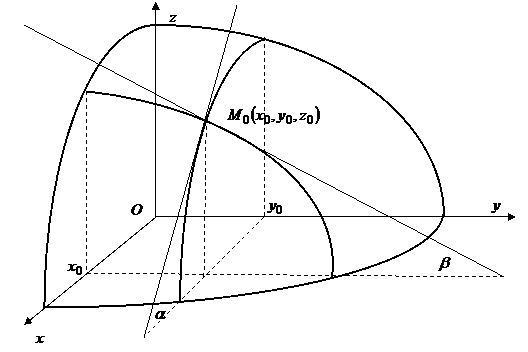Выясним геометрический смысл частных производных функции двух переменных. Геометрическим образом (графиком) функции является некоторая поверхность. Графиком функции 
является линия пересечения этой поверхности с плоскостью 
Исходя из геометрического смысла производной функции одной переменной, получаем, что, 
где a – угол между осью Ox и касательной, проведенной к пространственной кривой 
в точке 
Аналогично, 
где b – угол между осью Oy и касательной, проведенной к пространственной кривой 
(линии пересечения поверхности с плоскостью 
) в точке 
Приведем примеры вычисления частных производных первого порядка.
Пример 1. Найти частные производные функции 
Решение.
1.Считаем переменную y константой и применяем правила дифференцирования:
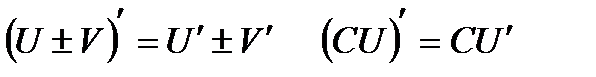
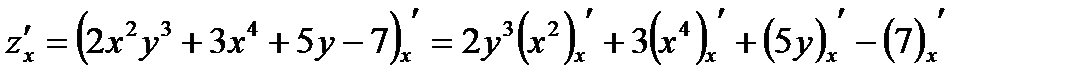
2. Используем табличные производные:
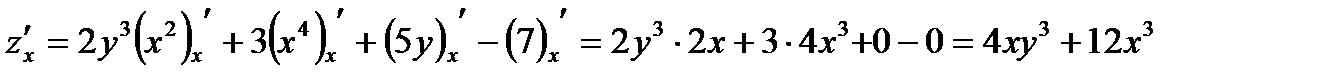
3. Теперь считаем переменную х константой и применяем те же правила дифференцирования и табличные производные:
Пример 2. Найти частные производные функции 
Решение.
1.Считаем переменную y константой и применяем правила дифференцирования:
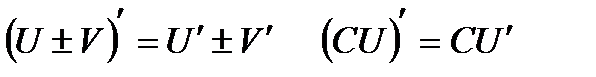
2. Используем табличные производные:
3. Теперь считаем переменную х константой и применяем те же правила дифференцирования и табличные производные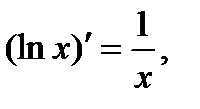 
:
Пример 3. Найти частные производные функции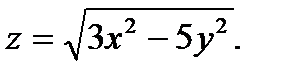 
Решение.
1. Считаем переменную y константой, применяем правило дифференцирования сложной функции, правило дифференцирования суммы, правило вынесение постоянного множителя за знак производной и табличные производные корня и степенной функции:
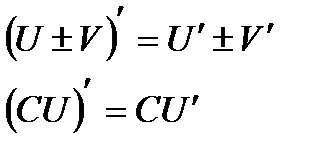
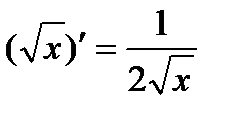
2. Теперь считаем переменную х константой и применяем те же правила дифференцирования и табличные производные:
