2017-10-31
5082
Пусть функция 
определена и непрерывна в некоторой ограниченной замкнутой области D. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области необходимо:
1. Найти критические точки функции , принадлежащие области D. Вычислить значения функции в критических точках.
2. Исследовать поведение функции на границе области D, найдя точки возможного наибольшего и наименьшего значений. Вычислить значения функции в полученных точках.
3. Из значений функции, полученных в предыдущих двух пунктах, выбрать наибольшее и наименьшее.
Пример
Найти наибольшее и наименьшее значения функции 
в ограниченной замкнутой области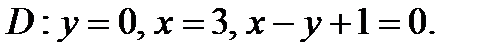 
Решение.
1) Изобразим заданную область на чертеже:
2) Найдём стационарные точки. Для этого вычислим частные производные первого порядка, приравняем к нулю и решим систему двух уравнений с двумя переменными:
|
|
|
Найденная стационарная точка принадлежит области 
Отметим точку на чертеже и вычислим значение функции в этой точке: 
3) Исследуем границу области (на чертеже постепенно отмечаем появляющиеся в ходе исследования точки):
Поскольку граница состоит из сторон треугольника, сначала рассмотрим отрезки, параллельные координатным осям, и в первую очередь – лежащие на самих осях.
Рассмотрим нижнюю сторону треугольника. Отрезок лежит на оси Ox, следовательно, все «игреки» точек отрезка равны нулю:
Геометрически это означает, что координатная плоскость xOz (которая тоже задаётся уравнением 
) «высекает» из поверхности «пространственную» параболу 
, вершина которой попадает под подозрение. Выясним, где она находится:
– полученное значение «попало» в область, и вполне может оказаться, что в точке 
функция достигает наибольшего либо наименьшего значения во всей области D. Находим значение функции в этой точке:
«Подозрительными» являются и концы отрезка. Вычислим значения функции в точках 
и 
:
Для исследования правой стороны треугольника подставляем 
в функцию
– полученное значение тоже попадает в область, а значит, нужно вычислить, чему равна функция в точке 
:
Исследуем второй конец отрезка 
:
Для исследования стороны 
подставим 
в функцию и упростим:
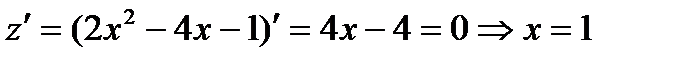
Подставляя 
в уравнение прямой 
получим ординату точки 
и находим соответствующее значение функции:
Итак,
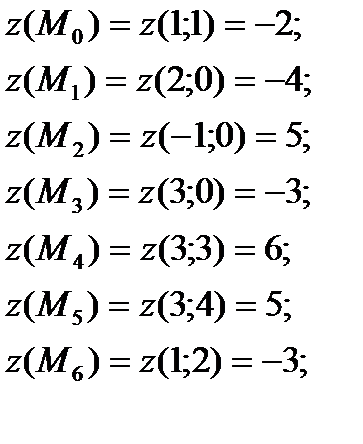
Из всех найденных значений выбираем наибольшее и наименьшее значения:
Геометрический смысл результата заключается в следующем:
|
|
|
– самая высокая точка поверхности в области D;
– самая низкая точка поверхности в области D.
