Предел и непрерывность функции двух переменных

Раздел 4. Основы математического анализа.

Тема 4.3 Дифференциальное исчисление функции нескольких действительных переменных.

Основные понятия.

При рассмотрении многих вопросов из различных областей знания приходится изучать такие зависимости между переменными величинами, когда числовые значения одной из них полностью определяются значениями нескольких других.

Например, изучая физическое состояние какого-либо тела, приходится наблюдать изменение его свойств от точки к точке. Каждая точка тела задается тремя координатами: x, y, z. Поэтому, изучая, скажем, распределение плотности, заключаем, что плотность тела зависит от трех переменных: x, y, z. Если физическое состояние тела к тому же еще и меняется с течением времени t, то та же плотность будет зависеть уже от значений четырех переменных: x, y, z, t.

Другой пример: изучаются издержки производства на изготовление единицы некоторого вида продукции. Пусть:

x - затраты по материалам,

y - расходы на выплату заработной платы работникам,

z - амортизационные отчисления.

Очевидно, что издержки производства зависят от значений названных параметров x, y, z.

В задачах математического программирования обычно разыскивается экстремум (максимум или минимум) целевой функции при некоторых ограничениях на значения ее переменных, которые записываются в виде системы уравнений и неравенств. Обычно целевая функция является функцией нескольких переменных.

Определение. Если каждой совокупности значений n переменных из некоторого множества D этих совокупностей соответствует своё единственное значение переменной z, то говорят, что на множестве D задана функция n переменных.

Множество D называется областью определения или областью существования этой функции.

Рассмотрим функцию двух переменных, так как все основные понятия и теоремы, сформулированные для функций двух переменных, легко обобщаются на случай большего числа переменных.

Определение. Если каждой паре (x,y) значений двух независимых друг от друга переменных величин x и y из некоторого множества D соответствует единственное значение величины z, а каждому z соответствует хотя бы одна пара (x,y), то мы говорим, что z есть функция двух независимых переменных x и y, определенная в D.

Если рассматривается функция двух переменных, то совокупности чисел обозначаются, как правило, (x, y) и интерпретируются как точки координатной плоскости Oxy, а область определения функции z = f (x, y) двух переменных изобразится в виде некоторого множества точек на плоскости Oxy.

Так, например, областью определения функции является множество точек плоскости Oxy, координаты которых удовлетворяют соотношению

т. е. представляет собой круг радиуса r с центром в начале координат.

Для функции

областью определения служат точки, которые удовлетворяют условию т. е. внешние точки по отношению к заданному кругу.

Часто функции двух переменных задаются в неявном виде, т. е. как уравнение

, связывающее три переменные величины. В этом случае каждую из величин x, y, z можно рассматривать как неявную функцию двух остальных.

Если функции одной переменной 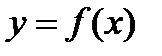соответствует определённая линия на плоскости (например, – всем знакомая школьная парабола), то график функции двух переменных 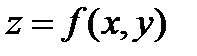располагается в трёхмерном пространстве. На практике чаще всего приходится иметь дело с поверхностью. Каждой паре ставится в соответствие точка принадлежащая графику функции и являющаяся концом перпендикуляра МР к плоскости Oxy.

 

Геометрическим изображением (графиком) функции двух переменных z = f (x, y) является множество точек P (x, y, z) в трехмерном пространстве Oxyz, координаты которых удовлетворяют уравнению z = f (x, y) (плоскости, цилиндры, шары, параболоиды и т.д.).

Графиком функции непрерывных аргументов, как правило, является некоторая поверхность в пространстве Oxyz, которая проектируется на координатную плоскость Oxy в область определения функции z= f (x, y).

Так, например, графиком функции является верхняя половина сферы, а графиком функции - нижняя половина сферы:

 

 

Графиком линейной функции z = ax + by + с является плоскость в пространстве Oxyz, а графиком функции z = сonst служит плоскость, параллельная координатной плоскости Oxyz.

Заметим, что функцию трех и большего числа переменных изобразить наглядно в виде графика в трехмерном пространстве невозможно.

Так же, как и при исследовании функций одной переменой, при рассмотрении функций нескольких переменных, важным моментом является отыскание области определения функции. Здесь полезно проводить некоторые аналогии, в частности, обращать особое внимание на те функции, в которых есть дроби, корни чётной степени, логарифмы и т. д.

Пример 1

Найти область определения функции .

Решение:

Так как знаменатель не может обращаться в ноль, то:

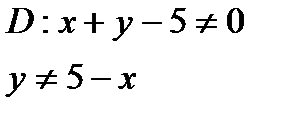
Уравнение задает на плоскости Oxy прямую, следовательно, областью определения заданной функции будет вся координатная плоскость Oxy, кроме точек, принадлежащих прямой .

Если бы по условию требовалось выполнить чертёж, то следовало бы изобразить координатную плоскость Oxy и пунктиром провести прямую Пунктир говорит о том, что линия не входит в область определения.

Пример 2

Найти область определения функции

Решение:

Подкоренное выражение должно быть неотрицательным:

Полученное неравенство задает полуплоскость, ограниченную снизу прямой

Пример 3. Найти и изобразить на чертеже область определения функции

Решение:

Подкоренное выражением должно быть неотрицательным и, учитывая, что знаменатель не может обращаться в ноль, получаем область определение, которая задается строгим неравенством:

Уравнение задает окружность радиуса 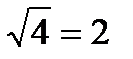с центром в начале координат, которая делит координатную плоскость на две части – внутреннюю и внешнюю области круга. Так как неравенство у нас строгое, то сама окружность не войдёт в область определения и поэтому её нужно провести пунктиром.

Теперь возьмем произвольную точку плоскости, не принадлежащую окружности 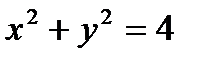, и подставляем её координаты в неравенство .

Проще всего выбрать начало координат

Получено неверное неравенство, таким образом, точка не удовлетворяет неравенству . Более того, данному неравенству не удовлетворяет и любая точка, лежащая внутри круга, и, стало быть, искомая область определения – внешняя его часть. Область определения традиционно штрихуется:

 

 

 

Пример 4.

Найти область определения функции

Решение:

Аргумент логарифма строго положителен, поэтому область определения задаётся системой

.

Неравенство задает на правую полуплоскость и исключает ось Oy.

Синус функция периодическая, промежутки знакопостоянства бесконечно чередуются и больше нуля синус на интервале .

Выполним чертёж, не забывая, что согласно первому условию, область определения ограничивается строго правой полуплоскостью.

 

Предел и непрерывность функции двух переменных.

Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывности, аналогично случаю функции одной переменной.

Введем понятие окрестности точки. Пусть на плоскости даны две точки и .

Определение. d (дельта)- окресностьюточки называется множество всех точек плоскости, расстояние от которых до точки меньше d, т.е. . Другими словами, d -окрестность точки - это все точки, лежащие внутри круга с центром и радиусом d. Обозначают d - окрестность точки символом

Определение. Число А называется пределом функции при и (или, что тоже самое, при ), если для любого существует такое , что для всех из d -окрестности точки 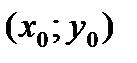причем 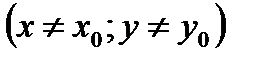выполняется неравенство .

Предел функции обозначается: 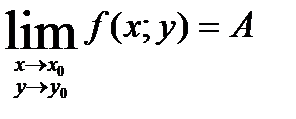. Т.е.

Нахождение предела функции двух переменных задача значительно более сложная, чем нахождение предела функции одной переменной. Задача усложняется из-за того, что для функции двух переменных на плоскости существует бесконечное множество направлений, по которым точка 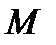может приближаться к точке В случае функции одной переменной таких направлений всего два: слева и справа. Нахождение некоторых пределов упрощается, если появляется возможность с помощью замены перейти к функции одной переменной.

Пример. Найти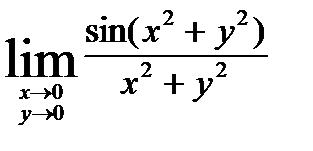

Решение.

Положим . Очевидно, что если и , то

Тогда

 

Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.

Определение. Функция называется непрерывной в точке если предел функции в этой точке существует и равен значению функции в этой точке:

Иначе говоря, функция непрерывна в точке если она:

1. определена в этой точке и некоторой ее окрестности;

2. существует конечный предел ;

3. выполнено равенство

Функция непрерывна в области,если она непрерывна во всех точках этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из условий непрерывности функции в точке, а именно в этой точке либо функция не определена, либо не существует предела, либо значение функции не равно значению предела) называются точками разрыва этой функции. Например, для функции точками разрыва являются точки прямой (их называют линиями разрыва).

Для функций двух переменных справедливы теоремы о непрерывных функциях одной переменной.

Свойство 1. Если функция определена и непрерывна в замкнутой и ограниченной области D, то в этой области найдется, по крайней мере, одна точка , такая, что для остальных точек верно неравенство:

а также точка , такая, что для всех остальных точек верно неравенство:

Тогда – наибольшее значение функции, а – наименьшее значение функции в области D.

Т.е. непрерывная функция в замкнутой и ограниченной области D достигает, по крайней мере, один раз наибольшего значения и один раз наименьшего.

Свойство 2. Если функция определена и непрерывна в замкнутой ограниченной области D, то она принимает в области D все промежуточные значения между M и m. Следствием этого свойства может служить заключение, что если числа M и m разных знаков, то в области D функция, по крайней мере, один раз обращается в ноль.

Свойство 3. Функция , непрерывная в замкнутой ограниченной области D, ограничена в этой области, если существует такое число К, что для всех точек области верно неравенство

Свойство 4. Если функция определена и непрерывна в замкнутой ограниченной области D, то она равномерно непрерывна в этой области, т.е. для любого положительного числа e существует такое число , что для любых двух точек и области, находящихся на расстоянии, меньшем d, выполнено неравенство: