Основне рівняння гідростатики

Основне рівняння гідростатики встановлює закон зміни гідростатичного тиску в даному об’ємі рідини, яка знаходиться в абсолютному спокої, тобто з масових сил на рідину діє тільки сила ваги.

Для виводу цього рівняння застосовуємо зведене диференціальне рівняння

Оскільки з масових сил діє тільки сила ваги, яка обумовлена прискоренням земного тяжіння “ g ”, то в рівнянні (23) Z = - g, а Х і Y дорівнюють нулю.

Тоді ; далі ділимо це рівняння на і -dz переносимо ліворуч

. (24)

рівняння (24) є основним рівнянням гідростатики в диференціальній формі.

Інтеграл цього рівняння при 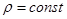буде:

= с, (25)

де z – відстань певної точки в об’ємі рідини густиною ρ з тиском p до площини порівняння.

Площина порівняння – це будь-яка горизонтальна площина, до якої заміряється положення вибраних точок в об’ємі рідини.

Розглянемо наступний приклад (рис. 4). Місткість з рідиною, на вільній поверхні якої тиск p _о. Знизу, як правило, проведена площина порівняння.

Позначимо через z₀ відстань від вільної поверхні рідини до площини порівняння. На відстані від площини порівняння z в точці всередині рідини тиск p.

Використовуючи рівняння (25) визначимо сталу інтегрування „ C” для випадку: при z₀, тобто на вільній поверхні, тиск - p₀. Тоді

Для двох точок, які знаходяться на відстані z і z₀ від площини порівняння рівняння запишеться:

. (26)

Звідси визначимо ;

;

так як z₀– z = h, то

, м ст. рідини, (27)

або

, [па]. (28)

Основне рівняння гідростатики (28) має такий зміст: тиск у будь-якій точці даного об’єму рідини дорівнює тиску на вільну поверхню рідини р₀ плюс тиск стовпа рідини () відповідно глибини занурення цієї точки під рівень вільної поверхні.

Основне рівняння гідростатики також формулює закон Паскаля про передачу тиску, що діє на вільну поверхню в будь-яку точку даного об’єма однаково. Тобто, тиск р₀ передається у всі точки даного об’єму рідини однаково, без будь-яких втрат. На основі закону Паскаля на виробництві застосовуються гідравлічні преси, домкрати, гідравлічні акумулятори.

Рис. 5

Основне рівняння гідростатики пов’язує між собою будь-які точки даного об’єму. Тобто для точок 1 і 2 (рис.5) можна записати рівняння відносно вибраної площини порівняння

. (29)

Геометричний зміст основного рівняння гідростатики. Розглянемо закриту місткість з рідиною, на вільній поверхні якої тиск р₀>р_ат _. Виберемо точки 1 і 2 в даному об’ємі рідини, які розташовані одна вище другої. Відстань цих точок до площини порівняння відповідно z₁ і z₂.

Над точками 1 і 2 встановимо скляні вертикальні трубки малого діаметра (d ≈ 5 мм), які відкриті знизу і зверху. На верхні кінці трубок діє атмосферний тиск. Ці трубки називаються п’єзометричними (або п’єзометрами).

Як показано на рис.6 в п’єзометричних трубках рідина піднята на один і той же самий рівень. Тобто вільні поверхні в трубках знаходяться в одній горизонтальній площині, але глибина занурення точок 1 і 2 під рівень вільних поверхонь різна. Глибина занурення точки 1 буде h₁, а точки 2 − h₂. Висота стовпа рідини в першій трубці h₁ буде створювати тиск р₁; або тиск р₁ піднімає рідину на висоту h₁. 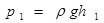Оскільки тиск р₁ створюється напором стовпа рідини h₁ густиною , то , або 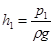, а h₂ – відповідно .

Вираз , що вимірюється в м стовпа рідини називається п’єзометричним напором.

В свою чергу z₁ і z₂ – геометричні напори, це є відстань від певних точок 1 і 2 до площини порівняння (в розділі „гідродинаміка” розглянемо енергетичний зміст цих величин). Як видно з рис. 6, сума двох напорів (геометричного і п’єзометричного) в різних точках в даному об’ємі рідини відносно площини порівняння є величина стала, що підтверджується основним рівнянням гідростатики ().