Розглядаються криволінійні поверхні, що занурені у рідину, які мають рівнодіючи. До таких криволінійних поверхонь відносяться сфери і їх частини, циліндричні поверхні і їх частини.
Розглянемо частину криволінійної поверхні, що представляє четверту частину сфери (рис. 16).
Координати ox, oy i oz. Проекція криволінійної поверхні на площину yoz буде площа „ б 0 г ”. Проекція криволінійної поверхні на площину хoz – площа „ а 0 г ”. Проекція криволінійної поверхні на площину хoу – площа „ а 0 б ”. Перші дві проекції – вертикальні, третя – горизонтальна.
В кожній точці криволінійній поверхні (абга), що занурена у рідину тиск різний, обумовлений глибиною занурення цих точок. Так як в межах елементарної поверхні (dF) тиск однаковий, то можна визначити елементарну силу тиску на цю елементарну площу, яка занурена на глибину h під рівень вільної поверхні (площина хоу)
 . (43)
. (43)
Елементарна сила направлена за нормаллю до елементарної площі dF. В координатній системі елементарна сила ( ) розташована під певними кутами до осей координат. Тоді цю елементарну силу можна розкласти (спроектувати) на складові відповідно осей координат, тобто
) розташована під певними кутами до осей координат. Тоді цю елементарну силу можна розкласти (спроектувати) на складові відповідно осей координат, тобто
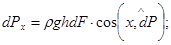


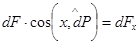 , тобто dFx – це проекція елементарної площі dF на площину „ у0z ”, до якої
, тобто dFx – це проекція елементарної площі dF на площину „ у0z ”, до якої  діє за нормаллю і направлено вздовж осі „ х ”;
діє за нормаллю і направлено вздовж осі „ х ”;
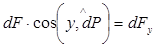 , dFy – проекція dF на площину „ x0z ”
, dFy – проекція dF на площину „ x0z ”
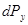 – направлена за нормаллю до площини „ x0z ”
– направлена за нормаллю до площини „ x0z ”
 , dFz – проекція dF на площину „ x0y ”.
, dFz – проекція dF на площину „ x0y ”.
 – направлена за нормаллю до площини „ x0y ” (рис.17).
– направлена за нормаллю до площини „ x0y ” (рис.17).
 Проекції елементарних сил на відповідні осі:
Проекції елементарних сил на відповідні осі:


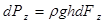
 Розглянемо елементарну силу
Розглянемо елементарну силу  , яка діє на проекцію елементарної криволінійної поверхні. dFx – вертикальна елементарна площадка, яка лежить в площині y0z. Тобто, це відповідає випадку визначення сили, що діє на вертикальну площу і ця сила направлена за нормаллю до площини дії (рис.18).
, яка діє на проекцію елементарної криволінійної поверхні. dFx – вертикальна елементарна площадка, яка лежить в площині y0z. Тобто, це відповідає випадку визначення сили, що діє на вертикальну площу і ця сила направлена за нормаллю до площини дії (рис.18).
 Тоді, аналогічно формулі (39), отримаємо
Тоді, аналогічно формулі (39), отримаємо
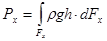
 (44)
(44)
де Fx – площа проекції криволінійної поверхні на вертикальну площину, „y0z”;
 hц.в . – глибина занурення центра ваги площі Fx під рівень вільної поверхні рідини.
hц.в . – глибина занурення центра ваги площі Fx під рівень вільної поверхні рідини.
Таким же самим чином визначаємо складову Ру

 (45)
(45)
де Fy – площа проекції криволінійної поверхні на вертикальну площину, „х0z”;
hц.в . – глибина занурення центра ваги площі Fу під рівень вільної поверхні рідини.
Визначаємо 
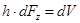 – елементарний об’єм рідини з елементарною площею dFz, яка розташована на горизонтальній площині Fz.
– елементарний об’єм рідини з елементарною площею dFz, яка розташована на горизонтальній площині Fz.
Fz – складається з сумарного значення dFz зі своїми висотами h.
Тому  представляє собою весь об’єм рідини, який знаходиться між криволінійною поверхнею, двома вертикальними площинами (x0z і „y0z) і горизонтальною площиною „х0у”.
представляє собою весь об’єм рідини, який знаходиться між криволінійною поверхнею, двома вертикальними площинами (x0z і „y0z) і горизонтальною площиною „х0у”.
Тобто, 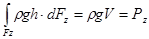 ,
,
де V – об’єм тіла тиску, тобто це той об’єм рідини, який тисне на криволінійну поверхню.
Так як 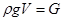 ,
,
де G – вага тіла тиску.
Тоді  . (46)
. (46)
 - вертикальна складова результуючої
- вертикальна складова результуючої 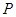 . Вона має направлення вниз, коли рідина налита в місткість і вверх, коли місткість занурена в рідину.
. Вона має направлення вниз, коли рідина налита в місткість і вверх, коли місткість занурена в рідину.
Оскільки знайдені складові  результуючої сили Р, то остання визначається як
результуючої сили Р, то остання визначається як
 . (47)
. (47)
Центр тиску результуючої „ Р ” на криволінійну поверхню.
Центром тиску на криволінійну поверхню називається точка перетину лінії дії результуючої, яка обумовлена певними кутами між результуючою і складовими, з криволінійною поверхнею (точка А). При цьому лінія дії  результуючої повина проходити через точку перетину ліній дій складових (точка а) (рис. 19). Лінія дії Pz проходить через центр ваги Fz об’єму тіла тиску V.
результуючої повина проходити через точку перетину ліній дій складових (точка а) (рис. 19). Лінія дії Pz проходить через центр ваги Fz об’єму тіла тиску V.
 2017-10-25
2017-10-25 488
488








