  |
| Рис.1 |
Задача 1. В закрытом сосуде находится вода  кг/м3, глубина наполнения сосуда
кг/м3, глубина наполнения сосуда  . Манометр на поверхности показывает давление
. Манометр на поверхности показывает давление  . На глубине
. На глубине  к сосуду присоединен пьезометр, атмосферное давление в открытом конце которого
к сосуду присоединен пьезометр, атмосферное давление в открытом конце которого  Па. Определить пьезометрическую высоту
Па. Определить пьезометрическую высоту 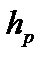 , абсолютное давление у дна и на поверхности сосуда. Построить эпюру абсолютного (полного) давления на плоскую боковую стенку BC в закрытом сосуде (рис.1). Ускорение свободного падения
, абсолютное давление у дна и на поверхности сосуда. Построить эпюру абсолютного (полного) давления на плоскую боковую стенку BC в закрытом сосуде (рис.1). Ускорение свободного падения  м/с2.
м/с2.
Решение задачи 1:
Примем 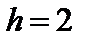 м,
м,  м,
м,  атм.
атм.
Так как жидкость находится в покое, то избыточное давление в сосуде на глубине  равно избыточному давлению регистрируемому пьезометром и определяется из основного уравнения гидростатики следующим образом
равно избыточному давлению регистрируемому пьезометром и определяется из основного уравнения гидростатики следующим образом
 ,
,
откуда пьезометрическая высота:
 м.
м.
Абсолютное давление на поверхности сосуда равно
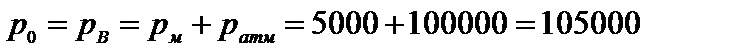 Па.
Па.
Для определения абсолютного давления у дна сосуда воспользуемся основным уравнением гидростатики:
 Па.
Па.
Эпюра дает графическое изображение изменения гидростатического давления вдоль поверхности. Так как абсолютное давление в точке боковой стенки закрытого резервуара у поверхности равно 1,05 атм, а в точке у дна – 1,35 атм, для построения эпюры абсолютного давления на плоскую боковую стенку необходимо восстановить перпендикуляры в удобном масштабе к точкам В и С у поверхности и дна, соединить концы перпендикуляров прямой линией, т. к. давление изменяется с глубиной линейно и направлено по нормали к площадке действия (рис.1).
 |
| Рис. 2 |
Задача 2. На поршень одного из сообщающихся сосудов (рис.2), наполненных водой, действует сила  , а на поршень второго сосуда
, а на поршень второго сосуда  . Определить разность уровней жидкости в сосудах
. Определить разность уровней жидкости в сосудах 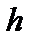 , если диаметр первого поршня
, если диаметр первого поршня 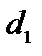 , второго поршня
, второго поршня  .
.
Решение задачи 2:
Примем  Н,
Н,  Н,
Н,  м,
м,  м.
м.
Давление на единицу площади на поверхности жидкости под первым поршнем
 атм.
атм.
То же, на поверхности жидкости под вторым поршнем
 атм.
атм.
Гидростатическое давление во втором сосуде на глубине  определяется по основному уравнению гидростатики
определяется по основному уравнению гидростатики  .
.
Так как жидкость находится в покое, можно записать  . Тогда
. Тогда  , откуда
, откуда
 м,
м,
где  кг/м3 – плотность воды;
кг/м3 – плотность воды; 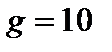 м/с2.
м/с2.
 |
| Рис. 3 |
Задача 3. Донное отверстие плотины перекрывается плоским прямоугольным щитом (рис.3), шарнирно прикрепленным к телу плотины своей верхней кромкой. Определить, какое усилие нужно приложить к тросу для открытия щита, если глубина погружения нижней кромки щита  , высота щита
, высота щита  , ширина щита
, ширина щита  , угол между направлением троса и горизонтом
, угол между направлением троса и горизонтом  .
.
Решение задачи 3:
Примем  м,
м, 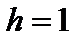 м,
м,  м,
м,  °.
°.
Давление воды на щит  определяем по формуле
определяем по формуле  , где площадь щита
, где площадь щита 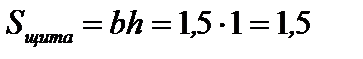 м2; глубина погружения центра тяжести щита
м2; глубина погружения центра тяжести щита  м.
м.
 кН.
кН.
Глубину погружения центра давления щита находим по формуле:
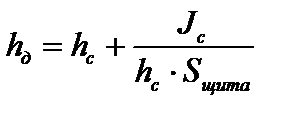 ,
,
где момент инерции площади щита
 м4,
м4,
тогда
 м.
м.
Усилие для открытия щита определится из равенства моментов  , откуда
, откуда
 ;
;
 м;
м;
 м,
м,
 кН.
кН.
 |
| Рис. 4 |
Задача 4. В призматическом сосуде шириной  установлена перегородка, имеющая в своей нижней части форму четверти цилиндрической поверхности с радиусом
установлена перегородка, имеющая в своей нижней части форму четверти цилиндрической поверхности с радиусом  (рис.4). Определить суммарное давление воды на криволинейную часть перегородки, если глубина воды слева
(рис.4). Определить суммарное давление воды на криволинейную часть перегородки, если глубина воды слева 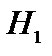 и справа
и справа  . Найти точку приложения равнодействующей давления воды.
. Найти точку приложения равнодействующей давления воды.
Решение задачи 4:
Примем  м,
м,  м,
м,  м,
м,  м.
м.
Горизонтальная составляющая давления воды слева

 кН.
кН.
Горизонтальная составляющая давления воды справа

 кН.
кН.
Вертикальная составляющая давления воды слева
 ,
,
где  – объем тела давления,
– объем тела давления,
 ,
,

 кН.
кН.
Вертикальная составляющая давления воды справа
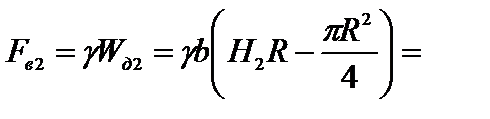
 кН.
кН.
Суммарное давление воды
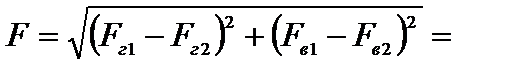
 кН.
кН.
Суммарное давление воды направлено перпендикулярно к поверхности перегородки, поэтому линия ее действия должна пройти через центр О. Угол наклона линии действия суммарного давления к горизонту определяем из соотношения
 ;
;  .
.
 |
Из центра О проводим линию под углом  к горизонту. Точка пересечения этой линии с перегородкой является точкой приложения равнодействующей давления воды.
к горизонту. Точка пересечения этой линии с перегородкой является точкой приложения равнодействующей давления воды.
Задача 5. Призматический сосуд длиной  шириной
шириной  заполнен водой на глубину
заполнен водой на глубину  (рис.5). Определить силы давления воды на переднюю и заднюю стенки сосуда при его горизонтальном перемещении с ускорением
(рис.5). Определить силы давления воды на переднюю и заднюю стенки сосуда при его горизонтальном перемещении с ускорением  .
.
 |
| Рис. 5 |
Решение задачи 5:
Примем 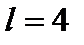 м,
м,  м,
м,  м,
м,  м/с2.
м/с2.
Понижение уровня воды у передней стенки и повышение уровня воды у задней стенки движущегося сосуда определяем по зависимости
 м.
м.
Глубина воды у передней стенки
 м.
м.
Глубина воды у задней стенки
 м.
м.
Сила давления воды на переднюю стенку
 кН.
кН.
Сила давления воды на заднюю стенку
 кН.
кН.
| Рис. 6 |
Задача 6. Определить, какой расход  протекает по горизонтальному трубопроводу, имеющему сужение (рис.6), при следующих данных: диаметры
протекает по горизонтальному трубопроводу, имеющему сужение (рис.6), при следующих данных: диаметры 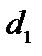 ,
, 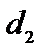 ; пьезометрические высоты
; пьезометрические высоты  ,
,  . Потери напора и неравномерность распределения скоростей в сечениях не учитывать.
. Потери напора и неравномерность распределения скоростей в сечениях не учитывать.
Решение задачи:
Примем  мм;
мм;  мм;
мм; 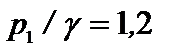 м;
м;  м.
м.
Напишем уравнение Бернулли без учета потерь для сечений 1-1 и 2-2 относительно плоскости сравнения, проходящей через ось трубопровода:
 .
.
Из уравнения неразрывности  имеем
имеем
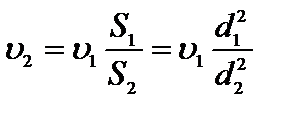 .
.
После подстановки значения для  в уравнение Бернулли получим
в уравнение Бернулли получим
 .
.
Решив последнее равенство относительно  , будем иметь
, будем иметь
 м/c.
м/c.
 м3/с.
м3/с.
 |
| Рис. 7. |
Задача 7. Из открытого резервуара, в котором поддерживается постоянный уровень, по стальному трубопроводу (эквивалентная шероховатость  мм), состоящему из труб различного диаметра
мм), состоящему из труб различного диаметра  и различной длины
и различной длины  , вытекает в атмосферу вода, расход которой
, вытекает в атмосферу вода, расход которой  , температура
, температура  °C. Определить скорости движения воды, потери напора (по длине и местные) на каждом участке трубопровода, величину напора
°C. Определить скорости движения воды, потери напора (по длине и местные) на каждом участке трубопровода, величину напора  в резервуаре. Построить напорную и пьезометрическую линии на всех участках трубопровода.
в резервуаре. Построить напорную и пьезометрическую линии на всех участках трубопровода.
Решение задачи:
Примем  м3/с;
м3/с;  м;
м;  м;
м;  м;
м;  м;
м;  м;
м;  м;
м;  °C.
°C.
Составим уравнение Д. Бернулли для каждого из сечений: 0-0, 1-1, 2-2, 3-3:


 .
.
Из уравнения неразрывности  выразим
выразим  ,
,  ,
,  .
.
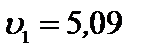 м/с (
м/с ( м2);
м2);
 м/с (
м/с ( м2);
м2);
 м/с (
м/с ( м2).
м2).
На первом участке трубопровода присутствуют местные потери на входе в трубу:
 м,
м,
где  , и потери напора по длине:
, и потери напора по длине:
 .
.
На втором участке трубопровода присутствуют местные потери на внезапное сужение:
 м,
м,
а потери напора по длине:
 .
.
На третьем участке трубопровода присутствуют местные потери на внезапное сужение:
 м,
м,
где 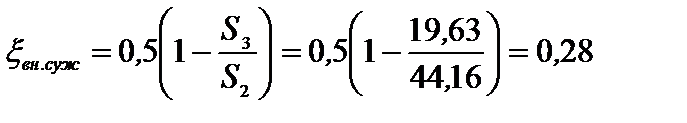 , а потери по длине:
, а потери по длине:
 .
.
Для определения потерь напора по длине вычислим числа Рейнольдса и установим режим движения на каждом участке трубопровода.
 ,
,
 ;
;  ;
;  ,
,
где кинематическая вязкость  рассчитана по формуле Пуазейля:
рассчитана по формуле Пуазейля:

 см2/с.
см2/с.
Следовательно, на втором участке имеет место область гидравлически гладких труб турбулентного режима, и значение  определяется по формуле Блазиуса:
определяется по формуле Блазиуса:
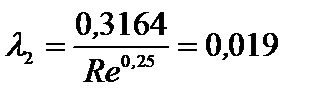 .
.
На первом и третьем участках значение  можно определить определяют по формуле Альтшуля:
можно определить определяют по формуле Альтшуля:
 ,
,
 .
.
Следовательно,
 м;
м;
 м;
м;
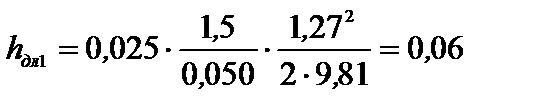 м.
м.
Величина напора составляет

 м.
м.
| Рис. 8 |
Задача 8. Определить время наполнения бассейна объемом  из магистрали с заданным давлением
из магистрали с заданным давлением  по горизонтальной трубе длиной
по горизонтальной трубе длиной  и диаметром
и диаметром  , снабженной вентилем
, снабженной вентилем  и отводом
и отводом  (рис.8). Коэффициент сопротивления трения определить по эквивалентной шероховатости
(рис.8). Коэффициент сопротивления трения определить по эквивалентной шероховатости 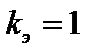 мм, предполагая наличие квадратичного режима.
мм, предполагая наличие квадратичного режима.
Решение задачи:
Примем 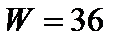 м3;
м3;  МПа;
МПа;  м;
м;  мм.
мм.
Напишем уравнение Бернулли для сечения 1-1 и 2-2 относительно оси трубопровода
 .
.
После приведения подобных членов получим
 ,
,
откуда
 .
.
Коэффициент сопротивления трения определяем по формуле Никурадзе
 ,
,
тогда
 м3/с.
м3/с.
Время наполнения бассейна
 c
c 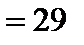 мин.
мин.
| Рис. 9 |
Задача 9. Определить диаметры труб для участков тупиковой водопроводной сети и установить требуемую высоту водонапорной башни в точке 1 для подачи следующих расходов в конечные пункты сети: 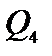 ,
,  ,
,  , и
, и  . Длины участков в метрах указаны на схеме сети (рис.9). Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор
. Длины участков в метрах указаны на схеме сети (рис.9). Местность горизонтальная. В конечных пунктах сети должен быть обеспечен свободный напор  м. При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб (табл.1).
м. При расчете воспользоваться значениями предельных расходов и расходных характеристик для новых водопроводных труб (табл.1).
Решение задачи:
Примем  л/с;
л/с;  л/с;
л/с;  л/с и
л/с и  л/с.
л/с.
1. Устанавливаем расчетные расходы для всех участков сети:
 л/с,
л/с,
 л/с,
л/с,
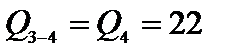 л/с,
л/с,
 л/с,
л/с,
 л/с,
л/с,
 л/с,
л/с,
 л/с.
л/с.
Таблица 1 – Значения предельных расходов
 2017-10-31
2017-10-31 6665
6665
