Математические конструкты для построения статистической модели

Фрагменты без предыстории изучаемого явления или процесса	Фрагменты с предысторией изучаемого явления или процесса
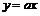- закон линейного роста или спада (при отрицательном знаке перед правой стороной приведенной формулы)	- закон не влияния принятой переменной на показатель, который имеет предысторию значений до периода измерений
- закон показательного роста (закон показательной гибели не является устойчивым, из-за бесконечности при нулевом значении объясняющей переменной	- закон Лапласа в математике (Ципфа в биологии, Парето в экономике, Мандельброта в физике) экспоненциального роста или гибели, относительно которого Лаплас создал метод операторных исчислений
- биотехнический закон (закон мастерства жизни) в упрощенной форме	- закон экспоненциального роста или гибели (П.М. Мазуркин)
- биотехнический закон, предложен проф. П.М. Мазуркиным

Примечание. Жирным шрифтом выделены полные математические конструкции.

В таблице 5/1 приведены все «нормальные» фрагменты, у которых впереди могут находиться оперативные константы в виде знаков «+» или «-». Шесть устойчивых законов распределения являются частными случаями биотехнического закона

Применение преобразований Лапласа ограничено. Поэтому аналитическое (дедуктивное) описание явлений и процессов может быть выполнено только при наличии в объектах исследования непрерывных, однородных и при этом информационно вполне определенных потоков.

Математический аппарат на преобразованиях Лапласа, предполагает описание явлений и процессов набором дифференциальных уравнений.

Но применительно к теории управления японский кибернетик Эйдзи Накано [93, с.49-51] предложил отказаться от непосредственного решения дифференциальных уравнений (рис. 5.1), а, воспользовавшись преобразованием Лапласа, перейти к решению алгебраических уравнений относительно оператора s.

Найденное решение алгебраического уравнения следует подвергнуть обратному преобразованию Лапласа, в результате чего и будет получено решение исходного дифференциального уравнения. Преобразование Лапласа применяется всегда, когда возникает необходимость перейти от свободной переменной дифференциальных уравнений t (времени) к переменной s. Физический смысл такого перехода заключается в том, что задачи, сформулированные во временной области, заменяются эквивалентными задачами, сформулированными в частотной области.

Рис. 5.1. Применение преобразований Лапласа

для решения систем дифференциальных уравнений [70, с.50, рис.3.6]

Причем, решению задачи временной области, представленной в виде дифференциального уравнения, соответствует решение частотной задачи, представленной алгебраическим уравнением.