К изменению параметров модели

Кроме нахождения оптимального решения прямой ЗЛП об использовании ресурсов необходимо получить дополнительную информацию о возможных (допустимых) изменениях решения при изменении параметров модели (например, при изменении запасов ресурсов или при изменении прибыли от единицы продукции). Эту часть исследования обычно называют анализом модели на чувствительность к изменению параметров. Он необходим в тех случаях, когда некоторые характеристики модели не поддаются точной оценке. В основе анализа модели на чувствительность лежит теорема об оценках.

Теорема 11.1 (теорема об оценках). Значения переменных в оптимальном решении двойственной ЗЛП (10.2) представляют собой оценки влияния свободных членов системы ограничений прямой

ЗЛП (10.1) на величину (на приращение целевой функции):

. (11.1)

Согласно теореме 11.1, двойственная оценка показывает меру влияния -го ограничения на целевую функцию прямой ЗЛП. Двойственная оценка численно равна изменению целевой функции при изменении соответствующего ресурса на единицу, то есть – это ценность дополнительной единицы -го ресурса. Двойственные оценки называют скрытыми оценками ресурсов.

Величина определяет ценность -го ресурса для производства: если мало, то его значительному увеличению будет соответствовать небольшое увеличение оптимального дохода; если же велико, то его незначительному увеличению будет соответствовать существенное увеличение оптимального дохода, ценность данного ресурса высока. Уменьшение ценного ресурса ведет к существенному сокращению выпуска продукции. Если (ресурс не является дефицитным), то при его увеличении оптимальный доход остается неизменным. Ресурс не представляет ценности для производства.

Пусть запас -го ресурса изменился на единиц, то есть запас -го ресурса составляет единиц. Из теоремы об оценках следует, что изменение величины приводит к изменению целевой функции на величину при условии, что значения двойственных оценок в оптимальном плане двойственной задачи (10.2) остаются неизменными. Поэтому необходимо найти интервал изменения коэффициента , при котором оптимальный план двойственной задачи (10.2) не меняется. Будем считать, что двойственные оценки не меняют своих значений, если не меняется набор переменных, входящих в базис оптимального плана прямой задачи (10.1), когда как значения самих базисных переменных в оптимальном плане могут меняться.

Приведем задачу (10.1) к каноническому виду путем введения балансовых переменных 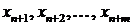. В матричном виде она имеет вид

(11.2)

где

Предположим, что задача (11.2) имеет оптимальное решение. Разобьем вектор на два вектора:

В первый вектор включены базисные переменные, вошедшие в оптимальный план задачи (11.2). Во второй вектор включены свободные переменные, так что (все компоненты вектора равны нулю). Соответственно матрицу представим в виде

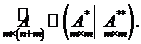
Матрицу 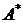размера формируют те столбцы матрицы , которые соответствуют базисным переменным в оптимальном плане.

Тогда система ограничений задачи (11.2) примет вид

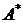Учитывая, что , последняя система примет вид Так как матрица неособенная, выразим из последнего равенства вектор-столбец :

(11.3)

где матрица . Матрица характеризует влияние ресурсов на величину оптимального выпуска продукции и используется при анализе задачи на чувствительность к изменению параметров.

Пусть вектор-столбец запасов ресурсов прямой задачи изменился на величину . Тогда пользуясь формулой (11.3), получим

откуда

. (11.4)

Формула (11.4) определяет величину структурных сдвигов в выпуске продукции при изменении ограничений прямой задачи.

Как было сказано выше, структура оптимального плана прямой задачи (10.1) не меняется, если не меняется оптимальный план двойственной задачи (10.2) (то есть оценки ресурсов не меняют своих значений).

Это возможно в том случае, когда среди компонент вектора нет отрицательных. С помощью матрицы и значений оптимального решения задачи (10.1) можно определить границы изменения ресурсов, при которых сохраняется структура оптимального плана. Предельные значения (нижняя и верхняя границы) ограничений ресурсов, для которых сохраняется структура оптимального плана, вычисляют по формулам

, , , (11.5)

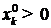где – элементы матрицы , – значение -й переменной в оптимальном решении прямой задачи, величины вычисляют с использованием только положительных элементов -го столбца матрицы , а величины – только отрицательных элементов -го столбца матрицы .

Пример 11.1. Определить предельные значения ограничений ресурсов из примера 10.1. Найти оптимальный план задачи, если запас ресурса труд увеличить на 12 единиц.

Решение. Выпишем исходные данные примера 10.1: вектор-столбец , матрица 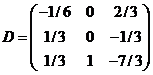. Оптимальное решение канонической задачи имеет вид . Тогда примем

, , .

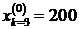Находим интервал устойчивости первого ресурса – труд. Вычисляем нижнюю и верхнюю границы интервала устойчивости:

В результате интервал устойчивости первого ресурса имеет вид

Находим интервал устойчивости второго ресурса – сырье. Так как этот ресурс является недефицитным (его двойственная оценка ), то его верхняя граница устойчивости равна 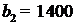. Нижняя граница

В результате интервал устойчивости второго ресурса имеет вид

Аналогично находится интервал устойчивости третьего ресурса

Найдем оптимальный план задачи, если запас ресурса труд увеличить на 12 единиц (эти изменения находятся в интервале устойчивости двойственных оценок). Используем формулу (11.4) для нахождения величину структурных сдвигов в выпуске продукции: