Кафедра высшей математики
СБОРНИК КОНТРОЛЬНЫХ РАБОТ И ИНДИВИДУАЛЬНЫХ ЗАДАНИЙ ПО ВЫСШЕЙ МАТЕМАТИКЕ
Пособие для студентов инженерных специальностей АГАУ

Барнаул 2002
УДК
Абакумова Н.А.,Зенков А.В., Кокшарова М.В, Колесникова Т.Г., Морозова С.В. Сборник контрольных работ и индивидуальных заданий по высшей математике - Барнаул: Изд-во АГАУ 2002 - с.
Программа по высшей математике для студентов инженерных специальностей предусматривает выполнение ряда индивидуальных заданий и контрольных работ.
Настоящий сборник содержит по 30 вариантов индивидуальных заданий по темам, причем подробно рассматривается решение одного из вариантов по каждому разделу. Также в сборник включены контрольные работы по основным разделам курса высшей математики.
Утверждено методическим советом ИТАИ. Протокол № от
Рецензент: к.ф.-м.н.И.В.Лёвкин
Индивидуальное задание № 1
по теме «Аналитическая геометрия на плоскости.»
В задачах 1 – 30 даны координаты вершин треугольника АВС. Найти:
1)длину стороны АВ;
2) уравнения сторон АВ и ВС и их угловые коэффициенты;
3) угол В в радианах с точностью до двух знаков;
4) уравнение высоты СД и её длину;
5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СД;
6) уравнение прямой, проходящей через точку К параллельно стороне АВ;
7) координаты точки М, расположенной симметрично точке А относительно прямой СД.
№ 1 А(-2;2), В(10;-7), С(14;15).
№ 2 А(-4;-1), В(8;-10), С(12;12).
№ 3 А(-7;1), В(5;-8), С(9;14).
№ 4 А(1;2), В(13;-7), С(17;15).
№ 5 А(-7;-1), В(-5;-10), С(9;12).
№ 6 А(0;3), В(12;-6), С(16;16).
№ 7 А(-8;4), В(4;-5), С(8;17).
№ 8 А(-2;2), В(10;-7), С(14;15).
№ 9 А(-3;0), В(9;-9), С(13;13).
№10 А(-6;-2), В(6;-11), С(10;11).
№11 А(-8;-3), В(4;-12), С(8;10).
№12 А(-5;7), В(7;-2), С(11;20).
№13 А(-12;-1), В(0;-10), С(4;12).
№14 А(-10;9), В(2;0), С(6;22).
№15 А(0;2), В(12;-7), С(16;15).
№16 А(-9;6), В(3;-3), С(7;19)
№17 А(1;0), В(13;-9), С(17;13),
№18 А(-4;10), В(8;1), С(12;23),
№19 А(2;5), В(14;-4), С(18;18),
№20 А(-1;4), В(11;-5), С(15;17),
№21 А(-2;7), В(10;-2), С(8;12),
№22 А(-6;8), В(6;-1), С(4;13),
№23 А(3;6), В(15;-3), С(13;11),
№24 А(-10;5), В(2;-4), С(0;10),
№25 А(-4;12), В(8;3), С(6;17),
№26 А(-3;10), В(9;1), С(7;15),
№27 А(4;1), В(16;-8), С(14;6),
№28 А(-7;4), В(5;-5), С(3;9),
№29 А(0;3), В(12;-6), С(10;8),
№30 А(-5;9), В(7;0), С(5;14).
Задание № 2. Какую линию определяет уравнение в задачах
1 – 30. Построить данную линию в декартовой системе координат.
№ 1) 2х2 – 4х + 2у – 3 = 0
№ 2) 2х2 + 5у2 – 12х + 10у + 13 = 0
№ 3) х2 - у2 + 6х + 4у – 4 = 0
№ 4) 4х2 + 9у2 – 24х + 36у + 36 = 0
№ 5) х2 – у2 – 4х – 6у – 9 = 0
№ 6) у2 – 10х – 2у – 19 = 0
№ 7) х2 – у2 + 4х + 2у – 6 = 0
№ 8) 2х2 + 5у2 – 8х – 2 = 0
№ 9 у2 – 6х + 14у + 49 = 0
№ 10) 16х2 +25у2 – 32х + 50у – 359 = 0
№ 11)  х2 -
х2 - 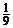 у2 – х +
у2 – х +  у – 1 = 0
у – 1 = 0
№ 12) х2 – 6х – 4у + 29 = 0
№ 13) 4х2 + 9у2 + 72х + 108 = 0
№ 14) 9х2 – 25у2 – 18х – 100у – 316 =0
№ 15) 4у2 – 6у – х + 11 = 0
№ 16) х2 – у2 – 2х – 3 = 0
№ 17) у2 + 4у – 6х + 7 = 0
№ 18) х2 + у2 – 2х + 4у –20 = 0
№ 19) 5х2 – 6у2 + 10х – 12у – 31 = 0
№ 20) 2х2 + 4у2 – 4х + 8у –10 = 0
№ 21) у2 + 8у – 2х + 10 = 0
№ 22) х2 – 2у2 – 2х + 8у – 17 = 0
№ 23) х2 + 4у2 + 4х – 24у + 36 = 0
№ 24) у2 – 4у + х – 6 = 0
№ 25) х2 – у2 – 4х + 2у – 4 = 0
№ 26) 2х2 + 3у2 – 4х + 6у – 7 = 0
№ 27) х2 –6х + у – 7 = 0
№ 28) х2 – 4у2 – 2х + 16у + 1 = 0
№ 29) 4х2 + 4у2 + 3у – 2 = 0
№ 30) х2 – 4у2 + 6х + 5 = 0
Решение типовых заданий:
Пример 1
Даны вершины треугольника АВС: А(-3;3), В(9;-6), С(7;8).
Найти: 1) длину стороны АВ;
2) уравнение сторон АВ и ВС и их угловые коэффициенты;
3) угол В в радианах;
4) уравнение высоты СД и её длину;
5) уравнение медианы АЕ и координаты точки К пересечения этой медианы с высотой СД;
6) уравнение прямой, проходящей через точку К параллельно стороне АВ;
7) координаты точки М, расположенной симметрично точке А относительно прямой СД.
Решение.
1) Расстояние  между точками А(х1;у1) и В(х2;у2) определяется по формуле
между точками А(х1;у1) и В(х2;у2) определяется по формуле  Применяя данную формулу, вычислим длину стороны АВ:
Применяя данную формулу, вычислим длину стороны АВ:

2) Уравнение прямой, проходящей через две данные точки А(х1;у1) и В(х2;у2), имеет вид:  . Подставляя в формулу координаты точек А и В, получим уравнение стороны АВ:
. Подставляя в формулу координаты точек А и В, получим уравнение стороны АВ:
 , или
, или  ; 12у – 36 = - 9х – 27.
; 12у – 36 = - 9х – 27.
Таким образом, общее уравнение прямой АВ имеет вид:
3х + 4у – 3 = 0.
Решив последнее уравнение относительно у, определим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом:  , откуда kАВ =
, откуда kАВ =  .
.
Аналогично определим уравнение стороны ВС и её угловой коэффициент:  ;
;  ; - 2у- 12 = 14х – 126;
; - 2у- 12 = 14х – 126;
7х + у – 57 = 0 – общее уравнение прямой ВС,
у = -7х + 57, откуда kВС = -7.
3) Тангенс угла  между двумя прямыми, угловые коэффициенты которых k1 и k2 вычисляется по формуле
между двумя прямыми, угловые коэффициенты которых k1 и k2 вычисляется по формуле
 . Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: kAB=
. Искомый угол В образован прямыми АВ и ВС, угловые коэффициенты которых найдены: kAB=  ; kBC=
; kBC=  , тогда
, тогда  .
.
 рад.
рад.
4) Так как высота CД перпендикулярна стороне AB, то угловые коэффициенты этих прямых обратны по величине и пртивоположны по знаку, т.е. kCД= 
Уравнение прямой проходящей через данную точку (х1;у1) в заданном угловым коэффициентом направлении, имеет вид:
у – у1 = k(х – х1). Подставим координаты точки С и kCД=  , получим уравнение высоты CД: у – 8 =
, получим уравнение высоты CД: у – 8 =  , 3у – 24 = 4х – 28, 4х – 3у – 4 = 0 – общее уравнение высоты CД. Для нахождения длины CД, вычислим координаты точки Д пересечения прямых АВ и CД, для этого решим систему из уравнений определяющих указанные прямые:
, 3у – 24 = 4х – 28, 4х – 3у – 4 = 0 – общее уравнение высоты CД. Для нахождения длины CД, вычислим координаты точки Д пересечения прямых АВ и CД, для этого решим систему из уравнений определяющих указанные прямые:  . Решим систему уравнений методом Крамера, для чего вычислим определители:
. Решим систему уравнений методом Крамера, для чего вычислим определители:
Δ =  = - 25; Δх =
= - 25; Δх =  = - 25; Δу =
= - 25; Δу =  = 0;
= 0;
Тогда решение системы имеет вид:  ;
;  , то есть положение точки Д определяется координатами (1;0). Вычислим длину высоты
, то есть положение точки Д определяется координатами (1;0). Вычислим длину высоты 
5) Чтобы найти уравнение медианы АЕ, определим сначала координаты точки Е, которая является серединой стороны ВС, применяя формулы деления отрезка на две равные части:
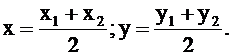
Следовательно, 
 то есть Е(8;1).
то есть Е(8;1).
Подставив в формулу уравнения прямой, проходящей через две данные точки, координаты точек А и Е, определяем уравнение медианы АЕ.



таким образом, 2х + 11у – 27 = 0 есть общее уравнение медианы АЕ.
Чтобы определить координаты точки пересечения высоты CД и медианы АЕ, решим систему уравнений, задающих указанные прямые.

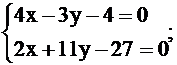
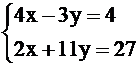 ; решая данную систему уравнений методом Крамера, вычислим Δ = 50, Δх = 125, Δу = 100, тогда
; решая данную систему уравнений методом Крамера, вычислим Δ = 50, Δх = 125, Δу = 100, тогда  ;
;  , то есть К(2,5;2) – точка пересечения высоты CD и медианы АЕ.
, то есть К(2,5;2) – точка пересечения высоты CD и медианы АЕ.
6) Так как искомая прямая параллельна стороне АВ, то её угловой коэффициент будет равен угловому коэффициенту прямой АВ, то есть  . Применяя формулу нахождения уравнения прямой, проходящей через данную точку в заданном направлении, получаем:
. Применяя формулу нахождения уравнения прямой, проходящей через данную точку в заданном направлении, получаем:  или
или  - общее уравнение искомой прямой.
- общее уравнение искомой прямой.
7) Так как прямая АВ перпендикулярна прямой CД, то искомая точка М, расположенная симметрично точке А относительно прямой CД лежит на прямой АВ. Кроме того, точка Д является серединой отрезка АМ. Применяя формулы деления отрезка на две равные части, вычисляем координаты точки М:
 , отсюда хМ = 5;
, отсюда хМ = 5;  , отсюда уМ= - 3.
, отсюда уМ= - 3.
То есть точка М имеет координаты (5;-3).
 Треугольник АВС, высота CД, медиана АЕ, прямая
Треугольник АВС, высота CД, медиана АЕ, прямая  , точка М построены в системе координат хОу на рисунке 1.
, точка М построены в системе координат хОу на рисунке 1.
Пример 2 Какую линию определяет уравнение 4х2+9у2+8х-36у+4=0. Построить данную линию в декартовой системе координат.
Решение. Сгруппируем слагаемые, содержащие х и у:
4х2+9у2+8х-36у+4=0.
(4х2+8х)+(9у2-36у)+4=0.
Вынесем за скобки из первого выражения 4, из второго – 9. Получим 4(х2+2х)+9(у2-4у)+4=0. В скобках добавим слагаемые, так чтобы получить формулу квадрата разности или квадрата суммы. Для того, чтобы равенство не изменилось, вычтем эти слагаемые после скобок.
4(х2+2х+1)+9(у2-4у+4)-4-36+4=0
4(х+1)2+9(у-2)2=36.
Поделим обе части равенства на 36, в результате получим:

Данное уравнение определяет эллипс, вершина которого находится в точке С(-1,2), при этом а2=9, следовательно а=3 и в2=4, следовательно в=2. Указанный эллипс построен в прямоугольной системе координат хОу на рисунке 2
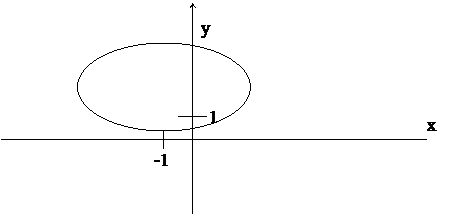 |
 2018-01-21
2018-01-21 1811
1811