Вопросы задают в тех случаях, когда есть познавательная неопределенность. Пусть, например, имеются города А и В. Наши войска находятся в городе В, а войска противника - в городе А. Города А и В соединены шестью дорогами (№ 1, № 2, № 3, № 4, № 5, № 6). Мы ждем наступления противника и хотим устроить засаду на тех дорогах, по которым пойдут его войска. Спрашиваем: «По каким дорогам пойдут войска противника?»
Задавая вопрос, мы знаем, что есть шесть дорог и что войска могут пойти по всем этим дорогам, или по какой-то одной, или по каким-то двум, трем и т.д. дорогам. Исходное знание, явно или неявно содержащееся в вопросе (его можно выразить посредством простого или сложного суждения), называется его предпосылкой. Предпосылка обусловливает множество возможных ответов на вопрос. Эту ситуацию можно проиллюстрировать так:
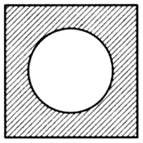
Заштрихованной поверхностью представлено имеющееся знание, а не заштрихованной - отсутствующее, т.е. познавательная неопределенность.
Допустим, что на заданный вопрос получен ответ: «Войска пойдут по дорогам № 1, № 4, № 5». (Установили, например, что на остальных дорогах имеются мосты, которые не выдержат технику противника, на которой он передвигается.) Ответ уменьшает исходную неопределенность. Графически:
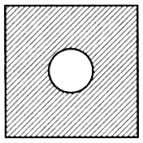
Таким образом, вопрос - это мысль, в которой выражается пожелание дополнить имеющуюся информацию с целью устранения или уменьшения познавательной неопределенности.
Характеризуя вопросы с логической точки зрения, следует рассматривать вопросно-ответные ситуации, включающие предпосылки вопросов. Благодаря последним вопросы могут использоваться для неявной передачи информации. Например, в вопросе «По какой причине студент Петров получил неудовлетворительную оценку на экзамене по логике?» содержится информация, что Петров - студент, он сдавал экзамен по логике и получил на экзамене оценку «неудовлетворительно». Тот факт, что вопросы имеют предпосылки, используется для совершения уловки «сокрытие необоснованности утверждения». Необоснованное утверждение выражается не явно, а в виде предпосылки вопроса. Например, вместо того чтобы обосновать целесообразность призыва студентов на военную службу, властям задают вопрос: «Когда же начнут призывать на военную службу студентов?»
Как реагировать на данную уловку? Нужно явно сформулировать предпосылку вопроса и сказать, что она является необоснованной, а также заметить, что совершена уловка «сокрытие необоснованности утверждения».
Другая уловка, связанная с предпосылками вопросов, имеет название «подмена вопроса». Она заключается в следующем. Пользуясь тем, что одним и тем же вопросительным предложением могут быть выражены разные вопросы из-за различия в подразумеваемых или содержащихся в контекстах предпосылках, заданный вопрос заменяют другим, или же ответ на один вопрос выдают за ответ на другой.
Примеры подмены вопросов:
(1) «Однажды стокгольмский епископ поехал в США по делам.
- Будьте осторожны с американскими журналистами, - напутствовали священника. - Там ради сенсации могут написать что угодно.
Поэтому, когда в Нью-Йорке нахрапистый репортер местной газеты с ходу задал епископу вопрос: „А не собираетесь ли Вы посетить места, где можно повеселиться ночью?“, тот опасливо спросил: „А что, здесь есть такие места?“
На следующий день газета вышла с интервью на первой странице под огромным заголовком: „Первый вопрос шведского епископа: есть ли в Нью-Йорке места, где можно повеселиться ночью?“»;
(2) «Местная молодежная газета „Юность“ решила прощупать пульс общественного мнения с помощью нехитрого социологического обследования. Приложили к газете отрывной талон с простенькими вопросами: „Как вы относитесь к строительству Ярославской АТЭЦ?“, „Если против, объясните, почему?“. Читатели прислали его в „Правду“ с вопросом: а где же „Если за...?“».
А ответ в самом талоне, который редакция снабдила крупным заголовком: „Ярославль - в Красную книгу?“. Я родился и вырос в Ярославле, люблю этот город и совсем не хочу, чтобы он значился в Красной книге. Но не хочу также, чтобы мои коллеги-журналисты под видом объективности навязывали свое мнение пусть меньшинству, но желающему взвешенно, всесторонне подойти к проблеме» (Покровский А. Неужели от лукавого? (Правда, 1989, 12 марта)).
В таких ситуациях нужно сказать, что совершена уловка «подмена вопроса», объяснить, в чем эта уловка заключается, и показать, какой вопрос был задан на самом деле или как надо было задать вопрос.
Логически корректные и логически некорректные вопросы. Вопрос является логически корректным, если на него можно дать истинный ответ, снижающий познавательную неопределенность. На логически некорректные вопросы такого ответа дать нельзя.
Различают несколько случаев логической некорректности вопросов.
Первый. В формулировке вопроса содержатся выражения, ни смыслы, ни значения которых не известны. Примером такового может служить следующий вопрос, заданный на лекции по логике студентами факультета психологии МГУ им. М.В. Ломоносова: «Приводят ли критическое метафизирование абстракциями и дискредитация тенденции церебрального субъективизма к игнорированию системы парадоксальных иллюзий?»
Второй. Все выражения, входящие в формулировку вопроса, имеют определенные смыслы или значения, однако между этими поражениями нет согласования. Пример: «Будете ли Вы проживать и Республике последние десять лет?»
Вопросы первого и второго типов являются бессмысленными.
Третий. В формулировке вопроса содержатся многосмысленные термины и из контекста не ясно, в каком из возможных смыслов они употребляются в данном случае. Такие вопросы называются недоопределенными.
Пример. «Вы за или против передачи земли народу?» Не ясно, что такое народ. Рабочие? Крестьяне? Все население страны? Не ясно, что понимается под передачей. Продать? Дать бесплатно? Дать тем, кто ее обрабатывает? Всем сельским жителям?
В процессе общения могут возникать ситуации, когда задаются вопросы, вообще-то являющиеся корректными, но воспринимаемые в качестве некорректных из-за того, что в их формулировках содержатся выражения, не известные данным лицам или данной аудитории или неправильно понимаемые. В таких случаях нужно или пояснить неизвестные или неправильно понимаемые выражения, или заменить известными.
Четвертый. На вопрос нельзя дать прямого истинного ответа. Предпосылкой вопроса является ложное суждение. Пример: «Перестал ли ты бить свою жену?». Предпосылкой этого вопроса является утверждение: «Ты бил свою жену, а сейчас перестал бить или продолжаешь бить».
Такие вопросы называются провокационными.
Посредством провокационных вопросов иногда ставят в затруднительное положение логически не подготовленных людей. Так, и ходе дискуссии о гуманизации уголовных наказаний противникам отмены смертной казни задавались вопросы: «Вы за неотвратимость наказаний или за их ужесточение?», «Вы лично, сейчас, здесь, готовы привести в исполнение смертный приговор?». На эти вопросы не было получено ответов.
Как следует отвечать на такие вопросы? Отвечая на первый вопрос, нужно отметить, что вопрос является логически некорректным, провокационным, поскольку его предпосылка «Человек должен выступать или за неотвратимость наказания, или за ужесточение наказания» является ложным утверждением. Затем целесообразно предложить исправить вопрос - «разбить» его на два вопроса: «Вы за неотвратимость наказания или против неотвратимости?», «Вы за смягчение наказания или за ужесточение, или за то, чтобы оставить действующие меры наказания?».
При ответе на второй вопрос тоже нужно сказать, что он является провокационным, и указать предпосылку: «Если человек не исключает возможность смертной казни в качестве высшей меры наказания, то он должен быть готов привести такой приговор в исполнение в любое время, в любом месте». Эта предпосылка является ложной.
Пятый. На вопрос нельзя дать ответа, снижающего познавательную неопределенность, поскольку таковой нет. Такие вопросы называются тавтологичными, причем различают логически тавтологичные и фактически тавтологичные вопросы.
Вопрос является логически тавтологичным, если запрашиваемая информация выражается его логической формой. Пример: «Является Сидоров тем человеком, которым он действительно является?» На такие вопросы нельзя дать ложного ответа, не являющегося логически противоречивым.
Вопрос является фактически тавтологичным, если запрашиваемая информация выражается всеми терминами, входящими в его формулировку, а не только логической формой. Пример: «Между кем и кем была русско-японская война?»
По степени неопределенности, которую требуется устранить, вопросы делятся на трудные и легкие. Например, одному студенту, стоящему около боевой машины пехоты (БМП), был задан вопрос: «Где находится дверь БМП?», а другому - «Где находится выхлопная труба БМП?» Второй не смог ответить. (Труба находится на крыше одного из типов БМП.)
Открытые и закрытые вопросы. К вопросам первого вида относятся те, которые не требуют определенного числа ответов. Закрытые вопросы требуют определенное число ответов. Различать эти вопросы важно при проведении социологических исследований посредством анкетирования. В анкеты в большинстве случаев должны включаться лишь закрытые вопросы.
Вопрос «Как читает лекции этот преподаватель?» - открытый. Его можно перестроить таким образом, чтобы получить закрытый вопрос (закрыть): «Как читает лекции этот преподаватель (хорошо, плохо, удовлетворительно)?».
Виды ответов. Среди истинных ответов важно различать правильные и неправильные. Правильными являются ответы, полностью или частично устраняющие познавательную неопределенность.
Ответ, полностью устраняющий познавательную неопределенность, называется сильным, не полностью - слабым. Из двух слабых ответов один может быть более сильным, чем другой. Например, на вопрос: «Кто является основателем науки логики?» - можно дать сильный ответ - «Аристотель» и слабые - «Древнегеческий философ», «Какой-то иностранец».
Правильные ответы могут быть также полными и неполными. Последние иногда даются на сложные вопросы, т.е. на вопросы, в которых можно выделить часть, в свою очередь являющуюся вопросом. Ответ на сложный вопрос является полным, если в нем содержатся ответы на все подвопросы этого сложного вопроса. Например, на вопрос: «Готов ли Верховный Совет взять власть в свои руки и осуществить экономическую реформу?» - депутат ответил: «Верховный Совет не может осуществить экономическую реформу, так как не разработана ее концепция». Ответ неполный: нет ответа на первую часть вопроса.
Неправильными являются ответы, не снижающие познавательной неопределенности. Они могут быть тавтологичными и нерелевантными.
Тавтологичные ответы могут быть истинными в силу логической формы (логически тавтологичные). Тогда они не несут фактической информации и в силу этого не могут снижать познавательную неопределенность. Например, на вопрос: «Будет ли жить больной?» отвечают: «Будет жить или нет». Фактически тавтологичные ответы истинны в силу того, что выражают информацию, содержащуюся в вопросе (полностью или частично повторяют предпосылку вопроса) или общеизвестную информацию. О таком ответе говорится в речи адвоката: «Защита... поставила перед техническим экспертом в суде прямой вопрос: с какой же скоростью должна была двигаться машина Фокина в конкретных условиях, предшествующих аварии, для того чтобы предотвратить возможность несчастного случая? Но эксперт ушел от ответа, прикрывшись расплывчатой фразой о „скорости, обеспечивающей безопасность движения“, т.е. перешел в область явной тавтологии»  .
.
Нерелевантными являются ответы не на заданные вопросы, а на другие.
В случае неправильного ответа, даваемого противоположной стороной в споре, нужно это отметить и указать, в чем заключается ошибка. Например, сказать, что ответ является нерелевантным, является ответом не на заданный вопрос, и повторить вопрос. Иногда полезно указать на слабость или неполноту правильного ответа. Важно и самому правильно задавать вопросы и отвечать на них.
4.3.
С. НОРМА
Нормы говорят, что некто обязан что-то сделать (или воздержаться от некоторого действия) или что кому-то разрешено (запрещено) определенное действие (или воздержание от действия).
Примерами предложений, выражающих нормы, являются следующие: «Гражданин России обязан соблюдать российские законы, где бы он ни находился - в России или за границей», «Запрещено проводить пропаганду войны».
Одно и то же предложение в зависимости от контекста может выражать как норму, так и утверждение о норме.
Например, в рассуждении:
«Гражданин России обязан соблюдать российские законы, где бы он ни находился - в России или за границей. Петров - гражданин России.
Следовательно, Петров обязан соблюдать российские законы, где бы он ни находился - в России или за границей».
Первое из предложений выражает утверждение о норме. Его можно истолковать так: «Гражданин России в соответствии с Конституцией обязан соблюдать российские законы, где бы он ни находился - в России или за границей». Или так: «Законодатель установил и не отменил, что гражданин России обязан соблюдать российские законы, где бы он ни находился - в России или за границей».
Утверждения о нормах являются суждениями и оцениваются как истинные или ложные.
Между нормативными понятиями «обязательно» (О), «запрещено» (З), «разрешено» (Р) существуют следующие зависимости:

Эти выражения соответственно читаются:
1. «обязательно А» эквивалентно «не разрешено не-А»;
2. «разрешено А» эквивалентно «не обязательно не-А»;
3. «обязательно А» эквивалентно «запрещено не-А»;
4. «запрещено А» эквивалентно «не разрешено А»;
5. «запрещено А» эквивалентно «обязательно не-А»;
6. «разрешено А» эквивалентно «не запрещено А».
5.
ГЛАВА IV. ДЕДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ. ВЫВОДЫ ЛОГИКИ ВЫСКАЗЫВАНИЙ
Умозаключение - это процесс получения знания, выраженного в суждении, из других знаний, тоже выраженных посредством суждений.
Исходные суждения называются посылками умозаключения, а получаемое суждение - заключением.
В логике исследуются умозаключения, осуществляемые на основе или с использованием особенностей логических форм посылок и заключений. Эти умозаключения делятся на дедуктивные и индуктивные. Название «дедуктивные умозаключения» происходит от латинского слова «deductio» («выведение»). В дедуктивных умозаключениях связи между посылками и заключением представляют собой формально-логические законы, в силу чего при истинных посылках умозаключение всегда оказывается истинным. Название «индуктивные умозаключения» происходит от латинского слова «inductio» («наведение»). Между посылками и заключением в этих умозаключениях имеют место такие связи по формам, которые обеспечивают получение только правдоподобного заключения при истинных посылках. Посредством дедуктивных умозаключений «выводят» некоторую мысль из других мыслей, а индуктивные умозаключения лишь «наводят» на мысль.
В процессе рассуждения иногда за дедуктивные принимают умозаключения, которые таковыми не являются. Последние называют неправильными дедуктивными умозаключениями, а (собственно) дедуктивные - правильными.
Выделение способов рассуждения, соответствующих правильным дедуктивным умозаключениям, - одна из центральных пройдем логики с момента ее возникновения. Однако в традиционной логике не были выработаны достаточно универсальные критерии правильности умозаключений, хотя было выделено большое число отдельных типов умозаключений, правильность которых очевидна или может быть обоснована с помощью несложных рассуждений.
Различают два вида дедуктивных умозаключений в зависимости от того, учитывается ли в них при осуществлении вывода внутренняя структура простых суждений, входящих в посылки и заключения, или нет. В этой главе описываются умозаключения, в которых при осуществлении вывода внутренняя структура простых суждений не учитывается, они называются выводами логики высказываний.
5.1.
§ 1. Учение традиционной логики о выводах логики высказываний
В традиционной логике изучались формы правильных и неправильных умозаключений наиболее простых видов: условно-категорические, разделительно-категорические, дилеммы и др. В условно-категорических умозаключениях одна посылка - условное суждение, основание и следствие которого являются категорическими суждениями, а другая посылка совпадает с основанием или следствием условного суждения или же с результатом отрицания основания или следствия условного суждения. В разделительно-категорических умозаключениях одна посылка - разделительное суждение, состоящее из двух категорических суждений, а другая посылка совпадает с одним из членов разделительного суждения или с его отрицанием. Будем называть условно-категорическими и разделительно-категорическими и те умозаключения, в которых членами сложных суждения являются любые суждения (не только категорические).
Условно-категорические умозаключения.
Пример.
Если это тело содержит свободные электроны, то оно является электропроводным. Это тело содержит свободные электроны.
_____________________________________________________________________
Оно является электропроводным.
Логическая форма этого умозаключения такова:

Умозаключения такой формы относятся к утверждающему модусу (modus ponens), а умозаключения формы

- к отрицающему модусу (modus tollens). Умозаключения этих логических форм являются правильными, а умозаключения, например, следующих форм:

неправильными. Эти правильные и неправильные способы рассуждения следует запомнить и различать.
Чтобы выяснить, является ли условно-категорическое умозаключение правильным или нет, нужно выявить его форму и установить, относится оно к одному из правильных модусов или нет. Если оно относится к правильному модусу, то оно правильное. В противном случае - неправильное.
Примеры.
Если существительное в предложении является подлежащим, то оно употреблено в именительном падеже. Существительное в предложении потреблено в именительном падеже.
_____________________________________________________________________
Оно является в предложении подлежащим.
Форма этого умозаключения:

Умозаключение неправильное.
Разделительно-категорические умозаключения.
Формы правильных разделительно-категорических умозаключении:

- утверждающе-отрицающий модус (modus ponendo-tollens);

отрицающе-утверждающий модус (modus tollendo-ponens).
Примеры умозаключений утверждающе-отрицающего модуса:
Это преступление совершено путем действия или же оно совершено путем бездействия. Это преступление совершено путем бездействия. Следовательно, оно не совершено путем действия.
Петров постоянно проживает в Москве или Архангельске. Он постоянно проживает в Москве. Следовательно, он не проживает постоянно в Архангельске.
Для установления правильности умозаключения рассматриваемого вида необходимо выяснить, относится ли оно к одному из правильных модусов. Если относится, то оно правильное. В противном» случае - неправильное.
Следует обратить внимание на то, что в умозаключениях утверждающе-отрицающего модуса в разделительном суждении союз «или» должен быть строго-разделительным. В противном случав умозаключение не будет правильным.
Иногда, исследуя умозаключения отрицающе-утверждающего модуса, не замечают, что разделительная посылка является ложной из-за того, что в ней перечислены не все возможные случаи. При ложной посылке заключение может оказаться ложным, хотя умозаключение является правильным.
Модусы правильных умозаключений рекомендуется запомнить.
Дилеммы. Название этих умозаключений происходит от греческих слов «ди» - дважды и «лемма» - предположение. Дилемма - это умозаключение из трех посылок: две посылки - условные суждения, а одна - разделительное суждение.
Дилеммы делятся на простые и сложные, конструктивные и деструктивные.
Формы правильных дилемм:

Эти схемы следует запомнить.
Примером простой конструктивной дилеммы может служить рассуждение Сократа:
Если смерть - переход в небытие, то она благо.
Если смерть - переход в мир иной, то она благо.
Смерть - переход в небытие или в мир иной.
_____________________________________________________________________
Смерть - благо.
Условные умозаключения. Посылками и заключениями этих умозаключений являются условные суждения.
Контрапозиция. Это умозаключение имеет следующую логическую форму:
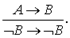
Пример.
Если философ - марксист, то он диалектик. Если философ не диалектик, то и не марксист.
Сложная контрапозиция. Схема:

Пример.
Если Иванов совершил преступление, предусмотренное ст. 156 УК, и он же совершил преступление, предусмотренное ст. 206 УК, то он подлежит наказанию по двум этим статьям.
Если Иванов совершил преступление, предусмотренное ст. 156 УК и он не подлежит наказанию по двум статьям - 156 и 206 УК, то он не совершил преступление, предусмотренное ст. 206 УК.
Транзитивность.

В традиционной логике рассматривался один вид наиболее простых умозаключений за другим и выделялись формы правильных умозаключений и формы неправильных. Учащимся предлагалось заучивать формы тех и других рассуждений. Недостатком этого способа изучения является то, что изучение занимает слишком много времени и не приводит к сколь-нибудь завершенному логическому образованию, поскольку правильных и неправильных способов рассуждений бесконечное множество.
Современная логика нашла несколько способов обзора бесконечного множества форм правильных рассуждений, относящихся к логике высказываний. Рассмотрим некоторые из них.
5.2.
§ 2. Учение современной логики о выводах логики высказываний. Классическая логика высказываний
Табличное построение логики высказываний.
Язык логики высказываний образуется из языка логики предиктов путем исключения из него ряда нелогических терминов.
Символы этого языка:
а)  ,... - пропозициональные символы (пропозициональные переменные);
,... - пропозициональные символы (пропозициональные переменные);
б)  - логические термины (логические константы);
- логические термины (логические константы);
в) () - скобки.
Определение ППФ:
а) пропозициональная переменная есть ППФ;
б) если А есть ППФ и В есть ППФ, то  - ППФ;
- ППФ;
в) ничто иное не есть ППФ.
Согласно определению, выражения (p q), 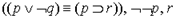 являются ППФ, а выражения
являются ППФ, а выражения  - нет.
- нет.
Примем соглашения об опускании скобок в формулах. Будем опускать внешние скобки у отдельно стоящей формулы. Условимся считать, что знак 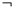 связывает теснее, чем знаки
связывает теснее, чем знаки  ; знак - теснее, чем
; знак - теснее, чем  - теснее, чем
- теснее, чем  теснее, чем
теснее, чем  . Исходя из сказанного, в формулах
. Исходя из сказанного, в формулах  , можно опустить скобки следующим образом
, можно опустить скобки следующим образом 
При табличном построении логики высказываний логические константы определяются посредством таблиц истинности. При этом принимается, что каждое высказывание имеет одно значение - или «истина», или «ложь».
Приведем эти табличные определения логических констант еще раз:
| А | 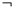 А А
|
| и л | л и |
| А | В | A&B | A  B B
| A 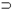 B B
| A  B B
|
| и и л л | и л и л | и л л л | и и и л | и л и и | и л л и |
В сложной формуле (формуле, содержащей логические термины) можно выделить логическую константу, называемую главной логической константой формулы. Такую формулу можно единственным образом представить в виде  Буквами А и В здесь обозначаются формулы, являющиеся частями сложной формулы. Подформулы (части формулы, являющиеся формулами), конечно, в свою очередь, могут быть сложными формулами.
Буквами А и В здесь обозначаются формулы, являющиеся частями сложной формулы. Подформулы (части формулы, являющиеся формулами), конечно, в свою очередь, могут быть сложными формулами.
Представив таким образом сложную формулу, мы выделяем в ней последнюю по построению логическую константу, которая и называется главной логической константой формулы.
Найдем главную логическую константу формулы  .
.
Восстановим скобки в этой формуле: 
Эту формулу единственным образом можно представить в форме  . Ее главным знаком является знак импликации.
. Ее главным знаком является знак импликации.
Можно представить в виде «дерева» процесс построения этой формулы:

Стрелки показывают, что из формул (или формулы), от которых ими направлены, образована формула, к которой они направлены. Цифры под логическими константами указывают порядковый номер константы по построению формулы. Последняя по построению константа имеет номер 5.
Построим таблицу истинности для формулы  . В таблице под главной константой формулы будем писать истинностные значения формулы в целом. В этой формуле главной логической константой является знак импликации. Чтобы установить истинностные значения всей формулы, необходимо установить истинностные значения подформул, составляющих ее, т.е. формул
. В таблице под главной константой формулы будем писать истинностные значения формулы в целом. В этой формуле главной логической константой является знак импликации. Чтобы установить истинностные значения всей формулы, необходимо установить истинностные значения подформул, составляющих ее, т.е. формул  . Истинностные значения этих формул будем соответственно писать под логическими константами
. Истинностные значения этих формул будем соответственно писать под логическими константами  В результате получим таблицу истинности:
В результате получим таблицу истинности:
| p | q | 
|
| и и л л | и л и л | и л л и и и и л л л и и |
Проанализируем первую строку таблицы. В первой строке пропозициональные переменные р и q имеют значение и. Чтобы установить истинностное значение формулы в целом, следует установить истинностные значения подформул  При значении и переменных р и q
При значении и переменных р и q  имеет значение и, при значении и переменной q формула
имеет значение и, при значении и переменной q формула  имеет значение л, что видно из таблиц истинности для дизъюнкции и отрицания, приведенных выше.
имеет значение л, что видно из таблиц истинности для дизъюнкции и отрицания, приведенных выше.
| p | q | 
|
| и | и | и л |
Оказывается, антецедент формулы в целом, являющейся импликацией, имеет значение и, а консеквент - л. В приведенной выше таблице для импликации в этом случае импликация имеет значение л:
| p | q | 
|
| и | и | и л л |
Можно упростить построение таблиц истинности, если значения пропозициональных переменных писать под переменными, входящими в саму формулу.
В приведенном выше табличном определении отрицания всего две строки, а в определениях для конъюнкции, дизъюнкции, импликации и эквивалентности - по четыре строки. Как установит число строк в таблице в общем случае, т.е. как установить, сколько может быть различных возможных наборов значений переменных, входящих в формулу?
Число строк в таблице истинности определяется по следующее формуле: число строк таблицы  , где n - число различных пропозициональных переменных, входящих в формулу, а число 2 показывает число истинностных значений (и, л).
, где n - число различных пропозициональных переменных, входящих в формулу, а число 2 показывает число истинностных значений (и, л).
Учитывая сказанное, построим таблицу истинности для формулы:

Формула содержит три различные переменные. Следовательно, число строк в таблице  Разделим число строк пополам и напишем под первой пропозициональной переменной (первой слева) в столбик четыре раза и и четыре раза л:
Разделим число строк пополам и напишем под первой пропозициональной переменной (первой слева) в столбик четыре раза и и четыре раза л:

Каждую половину всех строк, т.е. в данном случае каждые четыре строки, в свою очередь разделим пополам и напишем под второй по вхождению слева пропозициональной переменной, отличной oт первой пропозициональной переменной, в обеих половинах строк два раза и и два раза л:

Разделим, далее, половину каждой половины пополам и под ничьей по вхождению слева переменной, отличной от первых двух переменных, напишем и, если эта часть (строка) нечетная при пересчете сверху вниз, или л, если часть (строка) четная:

Деление производится до тех пор, пока полученная в результате деления часть не будет состоять из одной строки.
Одна и та же переменная может входить в формулу несколько раз. В одной и той же строке под всеми вхождениями одной и той же переменной пишется одно и то же значение, т.е. для завершения построения таблицы истинности следует под каждым вторым (третьим и т.д.) вхождением переменной написать те же значения, что и под первым вхождением этой переменной.

Несложно завершить построение таблицы истинности:

Эта формула имеет значение «истина» при каждом наборе значений входящих в нее переменных.
Формула, принимающая значение «истина» при любом набор значений входящих в нее переменных, называется тождественно-истинной, или законом логики, или общезначимой. Суждение этой формы называется логически необходимым.
Формула, принимающая значение «ложь» при любом набор значений входящих в нее переменных, называется тождественно-ложной, или противоречием. Суждение этой формы называется логически противоречивым.
Формула, принимающая значение «истина» хотя бы при некоторых наборах значений переменных, называется выполнимой. Если формула выполнимая, но не тождественно-истинная, то суждения этой формы называется логически случайным, или логически недетерминированным.
Логика высказываний, построенная табличным способом, дает эффективную процедуру для выявления законов логики, а также метод проверки правильности рассуждений. Рассуждение считается правильным, если между его посылками и заключением имеет место отношение логического следования. Определение:из посылок Г следует заключение В, если, и только если, импликация, имеющая антецедентом конъюнкцию формул, соответствующих посылкам, а консеквентом - формулу, соответствующую заключению, является тождественно-истинной.
Пусть дано рассуждение: «Если Иванов является участником этого преступления, то он знал потерпевшего. Иванов не знал потерпевшего, но знал его жену. Потерпевший знал Иванова. Следовательно, Иванов является участником этого преступления». Для определения правильности рассуждения требуется:
во-первых, обозначить различными символами различные простые высказывания, входящие в рассуждение. В приведенном рассуждении встречаются следующие простые высказывания: «Иванов является частником этого преступления», «Иванов знал потерпевшего», «Иванов знал жену потерпевшего». «Потерпевший знал Иванова». Обозначим их соответственно символами р, q, r, s;
во-вторых, перевести на язык логики высказываний посылки и заключение. Переводом посылок являются формулы  а переводом заключения - формула р (союз «но» соответствует в данном случае союзу «и»);
а переводом заключения - формула р (союз «но» соответствует в данном случае союзу «и»);
в-третьих, формулы, являющиеся переводом посылок, последовательно соединить знаком конъюнкции. Получаем формулу:

в-четвертых, к полученной формуле присоединить справа знаком импликации формулу, являющуюся переводом заключения. Получаем формулу:

в-пятых, для полученной формулы построить таблицу истинности.
Если формула, являющаяся переводом рассуждения на язык символов, оказывается тождественно-истинной, то можно сделать вывод о том, что рассуждение правильное, если тождественно-ложной, то рассуждение неправильное. Может оказаться, что формула является выполнимой, но не тождественно-истинной. В этом случае нет оснований считать рассуждение правильным. Необходимо продолжить анализ рассуждения, но уже средствами более богатого раздела логики - средствами логики предикатов.
Вернемся к рассматриваемому рассуждению. Построим таблицу истинности для формулы, являющейся переводом этого рассуждения на язык символов:

Формула является выполнимой, но не общезначимой. Следовательно, нет оснований считать рассматриваемое рассуждение правильным.
Если формула содержит много переменных, то в некоторых случаях можно не строить таблицу, а путем особых «сокращающих» рассуждений установить, является ли она общезначимой, противоречивой или же выполнимой, но не общезначимой.
Рассмотрим проанализированную выше формулу. Предположим, что при некотором наборе значений переменных она принимает значение «л»:

Это возможно, если значение консеквента есть «л», а антецедента - «и», а следовательно, каждого члена конъюнкции - «и»:

Поскольку переменной р уже приписано значение «л», пишем «л» под первым вхождением р в формулу:

Подформула  имеет значение «и», если, и только если,
имеет значение «и», если, и только если,  и r имеют значение «и»:
и r имеют значение «и»:

Поскольку подформула  имеет значение «и», под q пишем «л»:
имеет значение «и», под q пишем «л»:

Тогда

Формула принимает значения «л» при значениях «л», «л», «и», «и» соответственно переменных р, q, r и s.
Очевидно, что при значении «и» переменной р эта формула принимает значение «и». Формула принимает как значение «л», таки и значение «и», а следовательно, является выполнимой, но не общезначимой.
Рассмотрим формулу

Чтобы доказать, что формула является общезначимой, будем рассуждать от противного. Предположим, что она не общезначима, т.е. при некотором наборе значений переменных она принимает значение «л». Это возможно, если ее антецедент, а следовательно, каждый член конъюнкции принимает значение «и», а консеквет - «л»:

Приходим к противоречию, так как в этом случае, чтобы антецедент импликации оставался истинным, первому вхождению переменной q следует приписать значение «и», а второму - «л». Следовательно, формула является общезначимой.
Еще один способ установления отношения следования между суждениями, а также и других отношений, заключается в следующем:
· суждения переводятся на язык логики высказываний;
· для формул, соответствующих суждениям, строятся сравнимые таблицы истинности;
· устанавливаются виды отношений между суждениями на основе следующих определений:
· суждения совместимы по истинности, если и только если в сравнимых таблицах есть строка, в которой все формулы имеют значение «истина»;
· суждения совместимы по ложности, если и только если в сравнимых таблицах есть строка, в которой все формулы имеют значение «ложь»;
· из суждений  следует суждение В, если в сравнимых таблицах нет строки, в которой все формулы, соответствующие суждениям
следует суждение В, если в сравнимых таблицах нет строки, в которой все формулы, соответствующие суждениям  , имеют значение «истина», а формула, соответствующая суждению В, имеет значение «ложь».
, имеют значение «истина», а формула, соответствующая суждению В, имеет значение «ложь».
Остальные отношения являются производными по отношению к названным.
Пример. Пусть переводами трех суждений «Неверно, что ни один человек не захочет жить вечно, наука же откроет секрет физического бессмертия человека»; «Если наука откроет секрет физического бессмертия человека, то некоторые люди будут жить вечно или ни один человек не захочет жить вечно»; «Некоторые люди будут жить вечно» являются, соответственно, формулы  Построим для этих формул таблицы истинности таким образом, чтобы эти таблицы можно было сравнивать. Для этого выпишем вначале все переменные входящие в какие-либо из этих формул. Это переменные р, q, r. Число строк таблиц
Построим для этих формул таблицы истинности таким образом, чтобы эти таблицы можно было сравнивать. Для этого выпишем вначале все переменные входящие в какие-либо из этих формул. Это переменные р, q, r. Число строк таблиц  Строим таблицы:
Строим таблицы:

Между первыми двумя суждениями и последним имеет место отношение логического следования. Эти суждения (все три) совместимы по истинности (см. строку 5) и не совместимы по ложности.
5.2.1.
Исчисление высказываний. Система натурального вывода (СНВ)
Целью построения данного исчисления является создание логической системы, которую можно без больших сложностей использовать при исследовании естественных рассуждений. По этой причине правила вывода не являются минимальными. Автор стремился не к минимизации правил, а к их практической значимости. Кроме того, отдельные правила вывода (основные и производные) можно запомнить и применять при анализе рассуждений независимо от исчисления. Многие из этих правил известны по ранее изученному материалу данного учебника или соответствующему ему учебному курсу логики, а другие являются очевидными.
Язык логики высказываний приведен выше.
Кроме описания языка построение излагаемого ниже исчисления высказываний предполагает задание правил вывода двух родов и приведение определений вывода и доказательства выводимости.
Правила вывода первого рода (прямые правила).

Буквами А и В при формулировке правил обозначаются формулы.
Названия правил: ВК - введение конъюнкции, УК - удаление конъюнкции, ОК - отрицание конъюнкции, ВД - введение дизъюнкции, УД - удаление дизъюнкции, ОД - отрицание дизъюнкции, УИ - удаление импликации, ОИ - отрицание импликации, ВЭ - введение эквивалентности, УЭ - удаление эквивалентности, ВДО - введение двойного отрицания, УДО - удаление двойного отрицания.
Определение вывода. Выводом из множества гипотез (посылок, попущений) называется непустая конечная последовательность формул, в которой каждая формула есть или одна из гипотез, или формула, полученная из предшествующих формул последовательности по одному из правил вывода первого рода, или теорема (это понятие определяется ниже); вывод является выводом последней формулы этой последовательности, называемой заключением, из исходного множества гипотез.
Пусть Г - множество гипотез. В - последняя формула последовательности формул, являющейся выводом. Факт наличия вывода формулы В из множества гипотез Г записывается так: Г |- В. Последнее выражение называется утверждением о выводимости (или выводимостью, или непосредственно обоснованной выводимостью) формулы В из множества гипотез Г.
При осуществлении вывода справа от него пишется его анализ, т.е. указывается, на каком основании каждая из формул введена в вывод, например по какому правилу и из каких формул она получена.
Пример. Пусть требуется обосновать выводимость.

(1)  - посылка (далее посылки будем отмечать одним «плюсом», а допущения - двумя);
- посылка (далее посылки будем отмечать одним «плюсом», а допущения - двумя);
+(2) p q;
(3) р - из (2) по  ;
;
(4)  - из (1), (3) по
- из (1), (3) по 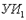 ;
;
(5) q - из (2) по  ;
;
(6) r - из (4), (5) по 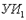 .
.
1.  - по определению вывода на основе (1)-(6).
- по определению вывода на основе (1)-(6).
Чаще всего бывает удобно в начале последовательности, являющейся выводом, выписать все посылки. Это, однако, не является обязательным. Посылки можно выписывать по мере надобности, причем из определения вывода следует, что одна и та же посылка может встречаться в выводе несколько раз. Некоторые из посылок вообще могут не встречаться в выводе, что проиллюстрируем на примере.
Пусть требуется обосновать выводимость 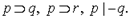
+(1) 
+(2) p;
(3) q - из (1), (2) по 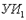 .
.
1. 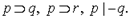 - по определению вывода на основе (1) - (3).
- по определению вывода на основе (1) - (3).
Правила вывода второго рода (непрямые правила):

Обозначения ПД, РОП, СА, РРС соответственно читаются: «правило дедукции», «рассуждение от противного», «сведение к абсурду», «рассуждение разбором случаев». Буквы А, В и D в формулировке правил обозначают формулы, а Г - множество формул (возможно, пустое).
Доказательством выводимости называется непустая конечная последовательность выводимостей, в которой каждая выводимость или является непосредственно обоснованной, или же получена из предшествующих выводимостей по одному из правил вывода второго рода. Доказательство является доказательством последней выводимости последовательности выводимостей. Выводимость, для которой имеется доказательство, называется обоснованной.
Формула А называется теоремой, если и только если существует обоснованная выводимость Г |- А такая, что множество гипотез Г пусто.
Эвристический прием: в последовательность выводимостей, являющуюся доказательством выводимости, можно включать ранее обоснованные выводимости.
5.2.2.
Эвристики
При обосновании выводимости Г |- В, где Г может быть пустым множеством, применяются следующие эвристики - приемы, облегчающие построение выводов и осуществления доказательств выводимостей.
Эвристика 1. Если главным знаком формулы В или ее последнего консеквента не являются знаки конъюнкции и эквивалентности, то в качестве допущения можно взять отрицание этой формулы. Разъяснение посредством примера: последним консеквентом формулы вида  является формула D.
является формула D.
Пример применения эвристики.
Пусть требуется обосновать выводимость  Рассуждаем «от противного». Выбираем в качестве допущения отрицание всей формулы, т.е. формулу
Рассуждаем «от противного». Выбираем в качестве допущения отрицание всей формулы, т.е. формулу  Строим вывод:
Строим вывод:
++(1) 
(2)  - из (1) по ОИ;
- из (1) по ОИ;
(3)  - из (2) по
- из (2) по  ;
;
(4)  - из (2) по
- из (2) по  ;
;
(5)  - из (4) по ОИ;
- из (4) по ОИ;
(6) q - из (5) по  ;
;
(7)  - из (5) по
- из (5) по  ;
;
(8)  - из (3), (7) по
- из (3), (7) по 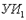 ;
;
(9)  - из (6), (8) по ВК.
- из (6), (8) по ВК.
1.  - по определению вывод на основе (1) - (9).
- по определению вывод на основе (1) - (9).
2.  - из 1 по РОП.
- из 1 по РОП.
Замечание 1. В учебных целях следует выписывать все шаги доказательства выводимости, однако после выработки навыков доказательств выводимостей можно записи сокращать. Очевидно, что если мы строим вывод посредством рассуждения от противного, то получение противоречия при допущении ложности утверждения лает основание завершить вывод и считать обоснованным рассматриваемое утверждение. Например, предшествующую последовательность формул и утверждений о выводимостях можно сократить так:

или даже так:
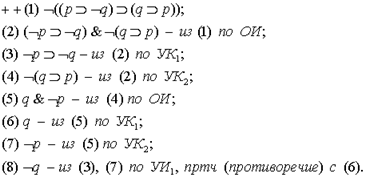
Замечание 2. Если В есть  , то вместо
, то вместо 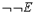 можно взять в качестве допущения Е.
можно взять в качестве допущения Е.
Пример. 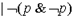

1.  - по определению вывода на основе (1).
- по определению вывода на основе (1).
2.  - из 1 по СА.
- из 1 по СА.
Сокращенно:
 .
.
Эвристика 2. Если главным знаком формулы В является знак импликации, а главным знаком ее последнего консеквента не являются знаки конъюнкции и эквивалентности, то в качестве допущений можно взять антецеденты этой формулы. Разъяснение посредством примера: пусть В есть  . Берем в качестве допущений формулы А, С и К.
. Берем в качестве допущений формулы А, С и К.
Пример. Требуется доказать теорему 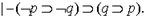

1.  - по определению вывода на основе (1) - (5).
- по определению вывода на основе (1) - (5).
2. 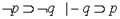 - из 1 по ПД.
- из 1 по ПД.
3.  - из 2 по ПД.
- из 2 по ПД.
Сокращенно:

Очевидно, какая часть рассуждения пропущена.
Эвристика 3. Если главным знаком формулы В является знак импликации, а главным знаком ее последнего консеквента не являются знаки конъюнкции и эквивалентности, то в качестве допущений можно взять антецеденты этой формулы, а также отрицание последнего консеквента.
Пример. Требуется доказать теорему 

1.  - по определению вывода на основе (1) - (5).
- по определению вывода на основе (1) - (5).
2.  - из 1 по ДОП.
- из 1 по ДОП.
3.  - из 2 по ПД (два применения).
- из 2 по ПД (два применения).
Сокращенно:

Замечание. Если последний консеквент В имеет вид  , то в качестве допущений можно взять антецеденты этой формулы, а также формулу Е.
, то в качестве допущений можно взять антецеденты этой формулы, а также формулу Е.
Пример. Требуется доказать теорему 

1.  - по определению вывода на основе (1) - (6).
- по определению вывода на основе (1) - (6).
2.  - из 1 по СА.
- из 1 по СА.
3.  - из (2) в результате двукратного применения ПД.
- из (2) в результате двукратного применения ПД.
Сокращенно:

Эвристика 4. Если главным знаком формулы В или главным знаком ее последнего консеквента является знак конъюнкции или эквивалентности, то иногда требуется осуществить два вспомогательных вывода.
Разъяснение посредством примеров.
Пример 1. Докажем схему теорем 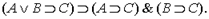

1.  - по определению вывода на основе (1)-(4).
- по определению вывода на основе (1)-(4).
2. 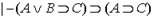 - из 1 в результате двукратного применения ПД.
- из 1 в результате двукратного применения ПД.
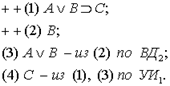
1. 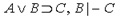 - по определению вывода на основе (1)-(4).
- по определению вывода на основе (1)-(4).
2.  - из 1 в результате двукратного применения ПД.
- из 1 в результате двукратного применения ПД.

1. 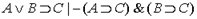 - по определению вывода на основе (1)-(6).
- по определению вывода на основе (1)-(6).
2.  - из 1 по ПД.
- из 1 по ПД.
Пример 2. Докажем схему теорем 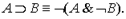

1.  - по определению вывода на основе (1)-(6).
- по определению вывода на основе (1)-(6).
2.  - из 1 по СА.
- из 1 по СА.
3.  - из 2 по ПД.
- из 2 по ПД.

1.  - на основе (1) - (6) по определению вывода.
- на основе (1) - (6) по определению вывода.
2.  - из 1 в результате двукратного применения ПД.
- из 1 в результате двукратного применения ПД.

1.  - на основе (1) - (3) по определению вывода.
- на основе (1) - (3) по определению вывода.
Эвристика 5. Если в выводимости или выводе есть формула  , то в качестве допущения можно взять А или В, или
, то в качестве допущения можно взять А или В, или 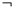 А, или
А, или 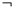 В.
В.
Пример. Докажем теорему 

1.  - по определению вывода на основе (1) - (16).
- по определению вывода на основе (1) - (16).
(В целях сокращения записи вместо формулы можно писать ее номер, например, последнее утверждение о выводимости можно записать так: 1. (1),  - по определению вывода на основе (1) - (16)).
- по определению вывода на основе (1) - (16)).
2. (1)  - из 1 по ДОК.
- из 1 по ДОК.
3.  - из 2 по ПД.
- из 2 по ПД.
И т.д. (Завершите доказательство.)
Эвристика 6. Обоснованные схемы выводимостей вида Г |- В, где Г - непустое множество, можно использовать в качестве производных правил вывода.
Пример. 

1.  - по определению вывода на основе (1) - (3).
- по определению вывода на основе (1) - (3).
2.  - из 1 по ПД.
- из 1 по ПД.
Производное правило контрапозиции:
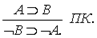
5.2.3.
Построение логики высказываний методом семантических таблиц
Еще одним способом установления отношений между высказываниями является использование семантических таблиц. Эти таблицы позволяют также выяснять, является ли та или иная формула общезначимой или нет, а тем самым определять, является ли логически истинным соответствующее ей высказывание или нет. Можно также установить, является ли формула противоречием, является ли она выполнимой, но не общезначимой.
Пусть в языке теперь отсутствует знак материальной эквивалентности (его можно ввести по определению:  ).
).
Семантическая таблица состоит из исходных формул, интерпретируемых как имеющие значение «истина», и формул, полученных из исходных посредством специальных правил, называемых правилами редукции и позволяющих из формул, интерпретируемых как имеющие значение «истина», получать формулы, тоже интерпретируемые как имеющие значение «истина».
В основе правил редукции лежат определения логических терминов. Для лучшего понимания этих правил заменим табличные определения логических терминов следующими определениями:
1) если Р - пропозициональная переменная, то  Функция
Функция  , функция приписывания значений формулам, приписываем пропозициональной переменной значение и или значение л.
, функция приписывания значений формулам, приписываем пропозициональной переменной значение и или значение л.
Если значения формул А и В, определены, то  (здесь и далее «
(здесь и далее « » читается «если и только если»);
» читается «если и только если»);
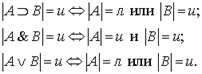
Пример 1. Пусть требуется установить, является ли формула  законом логики.
законом логики.
Будем рассуждать «от противного». Предположим, что эта формула не общезначимая, т.е. при некотором наборе переменных она имеет значение «ложь». Тогда формула  имеет значение «истина».
имеет значение «истина».
Если отрицание импликации истинно, то формула p q истинна, а р - ложна, т.е. формула 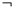 р истинна. Далее, если формула pq истинна, то истинно р и истинно q. Получили противоречие - формулы р и
р истинна. Далее, если формула pq истинна, то истинно р и истинно q. Получили противоречие - формулы р и 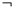 р истинны.
р истинны.
Таблица.

Пример 2. Рассмотрим формулу  Является ли она тождественно-истинной?
Является ли она тождественно-истинной?
Таблица:

Вертикальная черта означает, что следует учесть две возможности, то есть, если формула  истинна, то истинно
истинна, то истинно 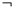 p или
p или 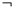 q (то есть ложна формула р или формула q). При наличии двух возможностей образуются две подтаблицы. В одну из этих подтаблиц входят формулы
q (то есть ложна формула р или формула q). При наличии двух возможностей образуются две подтаблицы. В одну из этих подтаблиц входят формулы  а в другую - формулы
а в другую - формулы  В первом случае имеется противоречие, а во втором - нет. Первая подтаблица замкнута, а вторая не замкнута. Можем сделать заключение, что исходная формула, т.е. формула
В первом случае имеется противоречие, а во втором - нет. Первая подтаблица замкнута, а вторая не замкнута. Можем сделать заключение, что исходная формула, т.е. формула  , не является тождественно-истинной и указать набор значений переменных, при котором она принимает значение «ложь». Эти значения - «истина» для р и «ложь» для q.
, не является тождественно-истинной и указать набор значений переменных, при котором она принимает значение «ложь». Эти значения - «истина» для р и «ложь» для q.
Является ли формула  тождественно-ложной? Опять рассуждаем «от противного». Предполагаем, что она может иметь значение «истина».
тождественно-ложной? Опять рассуждаем «от противного». Предполагаем, что она может иметь значение «истина».
Таблица:
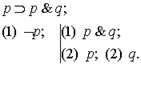
Таблица не замыкается. Получены два набора значений, при которых формула имеет значение «истина». Первый:  = л (a q может быть как истинно, так и ложно); второй:
= л (a q может быть как истинно, так и ложно); второй:  = и и
= и и  = и. Установлено, что формула является выполнимой, но не общезначимой.
= и. Установлено, что формула является выполнимой, но не общезначимой.
Сформулируем правила, позволяющие переходить от формул к другим формулам таблицы (правила редукции).
 (от формулы
(от формулы
 2018-01-21
2018-01-21 800
800







