Алфавит языка логики предикатов составляют следующие символы:
а)  - индивидные константы;
- индивидные константы;
б)  - индивидные переменные;
- индивидные переменные;
в)  - k-местные предметные функторы, знаки k-местных предметных функций (k = 1, 2, 3,...);
- k-местные предметные функторы, знаки k-местных предметных функций (k = 1, 2, 3,...);
г) 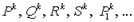 - k-местные предикаторные символы, или k-местные предикаторы (k = 1, 2, 3,...);
- k-местные предикаторные символы, или k-местные предикаторы (k = 1, 2, 3,...);
д)  - логические термины;
- логические термины;
е)  - логические термины;
- логические термины;
ж) (,) - скобки;
з), - запятая.
Определение терма:
а) индивидные константы и индивидные переменные являются термами;
б) если 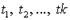 - термы, a
- термы, a  - k-местный предметный функтор, то выражение
- k-местный предметный функтор, то выражение 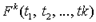 является термом;
является термом;
в) ничто иное не является термом.
Определение ППФ:
а) если  - термы, а
- термы, а  - k-местный предикатор, то
- k-местный предикатор, то  - ППФ;
- ППФ;
б) если А и В - ППФ, а  - индивидная переменная, то
- индивидная переменная, то  - ППФ;
- ППФ;
в) ничто иное не является ППФ.
Введем понятие подстановки терма вместо свободной индивидной переменной. Операция подстановки вместо индивидной переменной заключается в замене всех свободных вхождений переменной в формулу некоторым термом.
Подстановка терма вместо переменной  в формулу А называется правильной, если и только если: терм не является индивидном переменной и не имеет вхождений индивидных переменных; терм имеет вхождения индивидных переменных и все эти переменные после подстановки оказываются свободными в полученной из А формуле.
в формулу А называется правильной, если и только если: терм не является индивидном переменной и не имеет вхождений индивидных переменных; терм имеет вхождения индивидных переменных и все эти переменные после подстановки оказываются свободными в полученной из А формуле.
Вместо переменной х в формулу  можно подставить индивидную константу а -
можно подставить индивидную константу а - 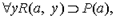 можно подставить, переменную z -
можно подставить, переменную z - 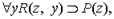 но нельзя подставить переменную y, так как после подстановки получаем формулу
но нельзя подставить переменную y, так как после подстановки получаем формулу  в которой первое вхождение переменной y в подформулу R(y, y) оказывается связанным (это вхождение является вхождением переменной, подставленной вместо переменной х).
в которой первое вхождение переменной y в подформулу R(y, y) оказывается связанным (это вхождение является вхождением переменной, подставленной вместо переменной х).
Правила вывода (первого и второго рода) исчисления высказываний (СНВ), применяемые к формулам языка логики предикатов
Дополнительные правила вывода первого рода:
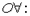  |   | |
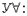 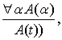 | где А(t) - результат правильной подстановки терма t вместо α в А (α); | |
  | где А(t) - результат правильной подстановки терма t вместо α в А (α); | |
  | где А (α) - результат правильной подстановки переменной α вместо β в А (β); α, β1, β2,..., β n отмечены, причем переменная α безотносительно отмечена, а переменные β1, β2,..., β n отмечены относительно α (последнее замечание поясняется ниже); β1, β2,..., β n - все свободные переменные формулы  | |
  | где А (α) - результат правильной подстановки переменной α вместо β в А (β); α, β1, β2,..., β n отмечены, α - безотносительно, а β1, β2,..., β n отмечены относительно α. β1, β2,..., β n - все свободные переменные формулы 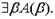 | |
Пояснения.
1. Буквами А и В при формулировке правил обозначаются формулы.
Выражение А( ) обозначает формулу, имеющую свободное вхождение переменной
) обозначает формулу, имеющую свободное вхождение переменной  , a A(t) - формулу, имеющую вхождение терма t.
, a A(t) - формулу, имеющую вхождение терма t.
2. Названия правил вывода расшифровываются так: О  - отрицание квантора общности; О
- отрицание квантора общности; О  - отрицание квантора существования; В
- отрицание квантора существования; В  - введение квантора общности; У
- введение квантора общности; У  - удаление квантора существования; В
- удаление квантора существования; В  - введение квантора существования; У
- введение квантора существования; У  - удаление квантора общности.
- удаление квантора общности.
3. Запись « отмечены» в примечании к правилу В
отмечены» в примечании к правилу В  означает, что
означает, что  безотносительно отмечена, а
безотносительно отмечена, а 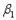 отмечена относительно
отмечена относительно  ;
;  отмечена относительно
отмечена относительно  ;
; 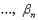 отмечена относительно
отмечена относительно  , или:
, или:  безотносительно отмечена и
безотносительно отмечена и  отмечает
отмечает 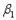 ;
;  отмечает
отмечает  и т.д.
и т.д.  - все свободные переменные формулы
- все свободные переменные формулы  Отношение «
Отношение « отмечает
отмечает  » является транзитивным, т.е. если
» является транзитивным, т.е. если  отмечает
отмечает  , а
, а  отмечает
отмечает 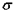 , то
, то  отмечает
отмечает 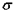 .
.
Поясним смысл выражений «переменная  безотносительно отмечена», «переменная
безотносительно отмечена», «переменная  отмечена относительно переменной
отмечена относительно переменной  ». Пусть дано выражение х
». Пусть дано выражение х  y. Областью значений переменных х и y является множество чисел {1, 2, 3, 4}. Применяя правило
y. Областью значений переменных х и y является множество чисел {1, 2, 3, 4}. Применяя правило  к исходному выражению, получим
к исходному выражению, получим  В исходном выражении переменная, например х, могла иметь условную интерпретацию (под x имелось в виду определенное число) или интерпретацию всеобщности (отношение
В исходном выражении переменная, например х, могла иметь условную интерпретацию (под x имелось в виду определенное число) или интерпретацию всеобщности (отношение  имело место для любых чисел из указанной области, мыслимых в качестве х). Если обе переменные выражения x
имело место для любых чисел из указанной области, мыслимых в качестве х). Если обе переменные выражения x  y имеют интерпретацию всеобщности, то вывод
y имеют интерпретацию всеобщности, то вывод  правомерен, поскольку в этом случае посылка (х
правомерен, поскольку в этом случае посылка (х  y) является ложной. (В самом деле, неверно, что для любого числа из указанной области, мыслимого в качестве х, и для любого числа из той же области, мыслимого в качестве y, верно, что х
y) является ложной. (В самом деле, неверно, что для любого числа из указанной области, мыслимого в качестве х, и для любого числа из той же области, мыслимого в качестве y, верно, что х  y.) Если же переменная х в x
y.) Если же переменная х в x  y имеет условную интерпретацию, то, применяя правило
y имеет условную интерпретацию, то, применяя правило  , мы производим переинтерпретацию этой переменной, придавая ей интерпретацию всеобщности. В этом случае, т.е. в случае переинтерпретации, переменная отмечается (безотносительно). Допустим, что в х
, мы производим переинтерпретацию этой переменной, придавая ей интерпретацию всеобщности. В этом случае, т.е. в случае переинтерпретации, переменная отмечается (безотносительно). Допустим, что в х  y переменная х находится в условной интерпретации, причем х приписано значение 4. Вводя квантор общности и переинтерпретируя переменную х, мы вынуждены переинтерпретировать переменную y, находящуюся, допустим, в интерпретации всеобщности. Чтобы выражение
y переменная х находится в условной интерпретации, причем х приписано значение 4. Вводя квантор общности и переинтерпретируя переменную х, мы вынуждены переинтерпретировать переменную y, находящуюся, допустим, в интерпретации всеобщности. Чтобы выражение  было верно, переменной у следует придать условную интерпретацию, а именно приписать значение 1. Таким образом, переменная y переинтерпретируется в результате переинтерпретации переменной х, поэтому она называется отмеченной относительно х.
было верно, переменной у следует придать условную интерпретацию, а именно приписать значение 1. Таким образом, переменная y переинтерпретируется в результате переинтерпретации переменной х, поэтому она называется отмеченной относительно х.
Смысл выражений «переменная  (безотносительно) отмечена и «переменная
(безотносительно) отмечена и «переменная  отмечена относительно
отмечена относительно  », входящих в примечание к правилу
», входящих в примечание к правилу  , тоже поясним на примере. Дано выражение
, тоже поясним на примере. Дано выражение 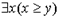 , область значений переменных та же, что и в предшествующем при мере, т.е. {1, 2, 3, 4}. Применяем правило:
, область значений переменных та же, что и в предшествующем при мере, т.е. {1, 2, 3, 4}. Применяем правило: 
Применение этого правила содержательно правомерно, если переменной х в заключение придать условную интерпретацию. Поскольку вывод в исчислении предикатов является формальным, может случиться так, что эта переменная будет рассматриваться как находящаяся в интерпретации всеобщности, что, вообще говоря, не всегда правомерно. Поэтому вводится примечание «переменная х отмечена», т.е., возможно, неправильно истолкована в качестве находящейся в интерпретации всеобщности.
Пусть, далее, в 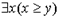 переменная у находится в интерпретации всеобщности. Истолковав переменную х, входящую в результирующее выражение х
переменная у находится в интерпретации всеобщности. Истолковав переменную х, входящую в результирующее выражение х  y, в качестве находящейся в интерпретации всеобщности, мы вынуждены, для получения истинного заключения из истинной посылки, придать переменной y условную интерпретацию, в данном случае приписать ей значение 1. Оба этих факта фиксируются записью «x, y отмечены» (x - безотносительно, а y - относительно х).
y, в качестве находящейся в интерпретации всеобщности, мы вынуждены, для получения истинного заключения из истинной посылки, придать переменной y условную интерпретацию, в данном случае приписать ей значение 1. Оба этих факта фиксируются записью «x, y отмечены» (x - безотносительно, а y - относительно х).
Таким образом выражение «переменная отмечена» означает (возможно) переинтерпретирована, а «отмечена относительно  » - возможно переинтерпретирована в результате переинтерпретации
» - возможно переинтерпретирована в результате переинтерпретации  .
.
Далее мы сформулируем специальные условия, касающиеся отмеченных переменных. Соблюдение этих условий гарантирует получение правильных выводов.
Выводом из множества гипотез (посылок, допущений) называется непустая конечная последовательность формул, в которой каждая формула есть или одна из гипотез, или формула, полученная из предшествующих формул последовательности по одному из правил вывода первого рода, или теорема (это понятие определяется ниже), если при построении этой последовательности ни одна переменная не отмечает сама себя (непосредственно или по транзитивности) и ни одна переменная не оказывается безотносительно отмеченной дважды; вывод является выводом последней формулы этой последовательности, называемой заключением, из исходного множества гипотез.
При осуществлении вывода справа от него будем писать не только его анализ, т.е. указывать, на каком основании каждая из формул введена в вывод, например по какому правилу и из каких формул она получена, но также указывать сведения, касающиеся отмечивания переменных.
Как было сказано, доказательством выводимости называется непустая конечная последовательность выводимостей, в которой каждая выводимость или является непосредственно обоснованной, или же получена из предшествующих выводимостей по одному из правил вывода второго рода. Выводимость, для которой имеется доказательство, называется обоснованной.
Замечание. Если при непосредственном обосновании выводимостей были отмечены переменные, то замечания об этом сохраняются и в результатах применения правил вывода второго рода. В связи с этим различаются полностью обоснованные выводимости и не полностью обоснованные выводимости. Выводимость является не полностью обоснованной, если и только если безотносительно отмеченная переменная входит свободно в одну из гипотез или заключение. В противном случае выводимость является полностью обоснованной.
Иногда в результате применения к не полностью обоснованной выводимости правила РОП или СА можно получить полностью обоснованную выводимость.
Пусть, например, требуется обосновать выводимость 

1.  по определению вывода на основе (1)-(13); х - отмечена (выводимость обоснована не полностью, так как безотносительно отмеченная переменная имеет свободное вхождение в заключение).
по определению вывода на основе (1)-(13); х - отмечена (выводимость обоснована не полностью, так как безотносительно отмеченная переменная имеет свободное вхождение в заключение).
2.  из 1 пo РОП; x отмечена (выводимость обоснована полностью).
из 1 пo РОП; x отмечена (выводимость обоснована полностью).
Если выводимость является полностью обоснованной, то замечания о том, что некоторые переменные были отмечены в процессе ее обоснования, считаются утратившими силу, т.е. могут быть опущены.
Формула А называется теоремой, если и только если существует полностью обоснованная выводимость Г |- A такая, что множество гипотез Г пусто.
Примеры обоснования выводимостей:
1. Установить, являются ли формулы вида 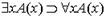 теоремами.
теоремами.

Получить обоснованную выводимость не удастся, поскольку одна и та же переменная оказывается безотносительно отмеченной дважды.
Попытаемся выбрать гипотезы другим способом:

Наталкиваемся на то же затруднение.
Замечание: читателю рекомендуется усвоить смысл отмечивания переменных; если это не удается, то можно принять на веру, что при соблюдении указанных требований относительно отмеченных переменных полностью обоснованными окажутся лишь выводимости, между посылками и заключением которых имеет место связь, представляющая собой логический закон, теоремами же будут только общезначимые формулы, т.е. формулы, выражающие логические законы.
2. 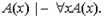
1.  - по определению вывода, х безотносительно отмечена.
- по определению вывода, х безотносительно отмечена.
Полностью обосновать выводимость не удается.
3. 

Установить, что выражение является схемой теорем, не удается, поскольку переменная х отмечает саму себя по транзитивности.
Для установления правильности рассуждения средствами СНВ рекомендуется: во-первых, обозначить символами нелогические термины. Пусть требуется осуществить анализ рассуждения: «Всякий, кто находится в здравом уме, может изучить логику. Ни один из сыновей Крокса не может изучить логику. Сумасшедшие не допускаются к голосованию. Следовательно, никто из сыновей Крокса не допускается к голосованию». В этом рассуждении встречается и то единичное имя - «Крокс». Введем для него символ а. Предикаторов в этом рассуждении четыре: «находящийся в здравом уме», могущий понимать логику», «сын», «допускаемый к голосованию». Введем для них соответственно символы Р, Q, R, S. При этом будем считать, что предикатор «сумасшедший» по смыслу совпадает с отрицанием предикатора «находящийся в здравом уме»;
во-вторых, перевести на язык логики предикатов посылки и заключение. Переводом посылок рассматриваемого рассуждения являются формулы

Переводом заключения - формула 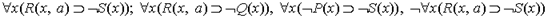
в-третьих, обосновать выводимость формулы, являющейся переводом заключения, из гипотез - формул, являющихся переводом посылок.
В рассматриваемом случае требуется обосновать выводимость


1.  - по определению вывода; х безотносительно отмечена.
- по определению вывода; х безотносительно отмечена.
2.  - из 1 по РОП; х безотносительно отмечена.
- из 1 по РОП; х безотносительно отмечена.
Если выводимость оказывается полностью обоснованной, то исследуемое рассуждение является правильным. Рассматриваемое рассуждение правильное. Если же не удается получить полное обоснование выводимости, то вопрос о правильности или неправильности рассуждения во многих случаях остается открытым, поскольку не существует общего метода, который позволял бы для любой выводимости получить ее полное обоснование или установить невозможность этого.
Посредством исчисления предикатов можно устанавливать не только отношение логического следования между высказываниями, но и другие отношения. Высказывания  несовместимы по истинности, если и только если
несовместимы по истинности, если и только если  где В - некоторая формула. Высказывания
где В - некоторая формула. Высказывания  несовместимы по ложности, если и только если
несовместимы по ложности, если и только если 
После создания символической логики возник вопрос: заменяет ли символическая логика традиционную? Если заменяет, то как переводить категорические суждения на язык логики предикатов для исследования силлогистических рассуждений? Изложенные в главе III способы переводов основаны на понимании категорических суждений Лейбницем. Согласно этому пониманию общие категорические суждения с пустыми субъектами являются истинными, а частные суждения с пустыми терминами - ложными. Силлогистика в смысле Лейбница называется фундаментальной.
Такое понимание категорических суждений не всегда является приемлемым, так как некоторые правильные с точки зрения традиционной силлогистики умозаключения не обосновываются. Например, умозаключение формы «Все М суть Р. Все М суть S. Следовательно, Некоторые S суть Р.» Чтобы решить эту проблему, следует учесть предпосылку традиционной силлогистики: термины силлогизмов не являются пустыми (мнимыми именами) и универсальными.
Выразим предпосылку следующим образом:

Тогда силлогизм анализируется так:

Предпосылка традиционной силлогистики о непустоте и неуни-иерсальности терминов категорических суждений распространяется на категорические суждения с отрицательными терминами, а также на суждения об отношениях. В последних субъекты тоже не должны быть мнимыми и универсальными именами. Отрицательные термины переводятся на язык логики предикатов путем отрицания атомарной формулы. Например, суждение «Тула есть не столица» можно перевести так:  а суждение «Тула не есть не столица» следующим образом:
а суждение «Тула не есть не столица» следующим образом: 
Пример. Является правильным умозаключение следующей формы?

Предпосылки традиционной силлогистики:

Перевод посылок и заключения на язык логики предикатов:

Несложно установить, что силлогизм является правильным.
 2018-01-21
2018-01-21 2494
2494
