Релевантная логика
В классической логике условные суждения заменяются импликативными. Это не приводит к недоразумениям в отдельных случаях. Например, если даны посылки вида А  В и мы заменяем их на посылки вида A
В и мы заменяем их на посылки вида A 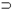 В, и получаем какое-то заключение, то и из исходных посылок это заключение тоже следует. Далее, в некоторых частных случаях можно из В получить суждение «если А, то В». Например, если крыши мокрые, то они являются мокрыми как при наличии дождя, так и при его отсутствии. В общем случае это, конечно, неверно, т.е. из В получить условное суждение «если А, то В нельзя. Так, не известна связь между свойствами животных: жвачность и парнокопытность. Пока наблюдается наличие парнокопытности в случае жвачности. Но верно ли, что наличие жвачности обусловливает наличие парнокопытное? Ясно, что если животное является жвачным, то из этого не следует необходимая связь этою свойства с парнокопытностью. Законы же науки утверждают необходимую связь признаков. Утверждения, выражающие законы вида А
В, и получаем какое-то заключение, то и из исходных посылок это заключение тоже следует. Далее, в некоторых частных случаях можно из В получить суждение «если А, то В». Например, если крыши мокрые, то они являются мокрыми как при наличии дождя, так и при его отсутствии. В общем случае это, конечно, неверно, т.е. из В получить условное суждение «если А, то В нельзя. Так, не известна связь между свойствами животных: жвачность и парнокопытность. Пока наблюдается наличие парнокопытности в случае жвачности. Но верно ли, что наличие жвачности обусловливает наличие парнокопытное? Ясно, что если животное является жвачным, то из этого не следует необходимая связь этою свойства с парнокопытностью. Законы же науки утверждают необходимую связь признаков. Утверждения, выражающие законы вида А  В не выразимы в классической логике.
В не выразимы в классической логике.
Кроме того, в классической логике материальная импликация понимается как аналог логического следования. В отдельных случаях такое соответствие допустимо. В общем же случае материальная импликация не соответствует интуитивно понимаемому отношению логического следования. Законы классической логики  трактуются как парадоксы материальной импликации: «если А ложно, то из А следует любое высказывание» и т.д. Известно также, что логически истинное высказывание следует из любого высказывания, а из противоречивого высказывания следует любое высказывание. Как объяснить и преодолеть эти ситуации? Еще в 1918 г., как уже было сказано, К.И. Льюис построил одну из систем строгой импликации, а затем еще ряд систем со строгой импликацией. Однако оказалось, что в системах S2 - S5 доказуемы формулы
трактуются как парадоксы материальной импликации: «если А ложно, то из А следует любое высказывание» и т.д. Известно также, что логически истинное высказывание следует из любого высказывания, а из противоречивого высказывания следует любое высказывание. Как объяснить и преодолеть эти ситуации? Еще в 1918 г., как уже было сказано, К.И. Льюис построил одну из систем строгой импликации, а затем еще ряд систем со строгой импликацией. Однако оказалось, что в системах S2 - S5 доказуемы формулы  и т.д. То есть системы со строгой импликацией тоже оказались парадоксальными.
и т.д. То есть системы со строгой импликацией тоже оказались парадоксальными.
В 1956 г. Аккерман опубликовал систему с сильной импликацией. (Вообще-то эта система тоже называется системой со строгой импликацией «Strenger Implication», но ее назвали системой с сильной импликацией при переводе на русский язык, чтобы отличить от систем Льюиса.) В этой системе импликация  соответствует выражению «если..., то...» в предложениях, выражающих законы науки, и отношению логического следования, понимаемого как связь между высказываниями по информации. Потом результат переформулировки этой системы был назван системой Е (of entailment - следования). Это система релевантной логики.
соответствует выражению «если..., то...» в предложениях, выражающих законы науки, и отношению логического следования, понимаемого как связь между высказываниями по информации. Потом результат переформулировки этой системы был назван системой Е (of entailment - следования). Это система релевантной логики.
Исчисление Е
Схемы аксиом:

N - знак необходимости.
Правила вывода:

Как осуществляется переход от классической логики к релевантной? Ограничимся отношением релевантного следования между формулами, содержащими логические термины 
Что понимается под отношением логического следования? Это отношение должно обладать, по крайней мере, следующими свойствами:
1) отношение устанавливается по логическим содержаниям высказываний (вспомним, что содержание высказывания делится на логическое и полное);
2) это отношение между посылками  и заключением В имеет место, если, и только если, логическое содержание В есть часть логического содержания множества высказываний {
и заключением В имеет место, если, и только если, логическое содержание В есть часть логического содержания множества высказываний {  }.
}.
Е.К. Войшвилло предложил понимать логическое содержание высказывания как семантическую информацию, выражаемую его логической формой, а «отношение логического следования как отношение между высказываниями по информации»  .
.
Информация высказывания рассматривается как степень ограничения некоторого множества возможностей в результате принятия высказывания за истинное. Чтобы сравнивать высказывания по информации, их информацию нужно привести к «общему знаменателю», т.е. рассматривать информации высказываний относительно некоторого общего множества возможностей М.
Будем выражать информацию высказывания А относительное множества возможностей М (пишем: I(А, М)) так: ( , М), где
, М), где  и М - множество строк таблицы истинности (множество описаний состояний), в которых формула А истинна, и множество всех строк таблицы для формулы (множество всех описаний состояний для формулы), соответственно. Например, информация высказывания p
и М - множество строк таблицы истинности (множество описаний состояний), в которых формула А истинна, и множество всех строк таблицы для формулы (множество всех описаний состояний для формулы), соответственно. Например, информация высказывания p  q может быть выражена так. В таблице истинности для этой формулы четыре строки. Заменим строки описаниями состояний:
q может быть выражена так. В таблице истинности для этой формулы четыре строки. Заменим строки описаниями состояний:  есть {р, q};
есть {р, q};  есть
есть  есть
есть  есть
есть  Приведенная формула истинна в первых трех описаниях состояний. Таким образом,
Приведенная формула истинна в первых трех описаниях состояний. Таким образом,  есть
есть 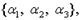 a М -
a М -  есть
есть 
Отношение логического следования определяется так:
 есть часть
есть часть  Поскольку
Поскольку  и
и  соответственно понимаются как множества описаний состояний, в которых истинны формулы А и В, отношение логического следования можно определить так:
соответственно понимаются как множества описаний состояний, в которых истинны формулы А и В, отношение логического следования можно определить так:
 (Выражения
(Выражения  соответственно читаются «истинно А в описании состояния
соответственно читаются «истинно А в описании состояния  » и «ложно А в описании состояния
» и «ложно А в описании состояния  ».
».
Введем определения значений истинности, соответствующие табличным определениям.
1. Если Р - пропозициональная переменная, 
Пусть значения формул А и В установлены. Тогда:

Кроме этих определений в классической логике принимаются условия для строк таблицы (для описаний состояний):

На основе условия (а) доказуемо: 

На основе условия (б) доказуемо: 
«Добавление предпосылок (а) и (б) к определениям логических связок означает, что, определяя информацию высказываний [например, высказывания А. - Ю.И.], мы имеем в виду фактически не логические их содержания, не ту информацию, которую содержит логическая форма (А) высказывания сама по себе, а так называемую привнесенную информацию, т.е. такую информацию, которую А добавляет имеющимся у нас знаниям о мирах, а именно к знанию, которое представляет Г - совокупность указанных предпосылок (а) и (б»  1?????.
1?????.
Информация высказывания самого по себе может отличаться от информации с учетом Г. Если в Г содержится информация, выражаемая А, то информация А с учетом Г равна нулю. Это и объясняет этот факт: законы классической логики не несут информации, противоречивое высказывание несет информацию о любом высказывании.
Чтобы выявить логическую информацию высказывания самого по себе, нужно отвлечься от Г, т.е. от предпосылок (а) и (б). Отвлечение от этих предпосылок приводит к изменению понятия описания состояния. Измененное таким образом описание состояния называется обобщенным описанием состояния. Обобщенное описание состояния - это любое подмножество множества  все пропозициональные переменные, входящие в рассматриваемые формулы. Так, обобщенными описаниями состояний для формулы р
все пропозициональные переменные, входящие в рассматриваемые формулы. Так, обобщенными описаниями состояний для формулы р 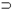 р являются: {р}, {
р являются: {р}, { 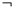 р}, {р,
р}, {р, 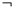 р}, {}. В последнем случае предполагается, что нет информации о р. Обобщенными описаниями состояний для формулы (формул), содержащей переменные р и q, являются
р}, {}. В последнем случае предполагается, что нет информации о р. Обобщенными описаниями состояний для формулы (формул), содержащей переменные р и q, являются
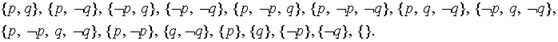
Множество обобщенных описаний состояния будем обозначать буквой М.
Принимая принципы классической логики, принимают знание В мире: в мире положение дел обязательно имеет место или отсутствует, событие не может одновременно иметь место и не иметь места и др. При построении релевантной логики происходит отвлечение от этих знаний о мире.
Принципы классической и релевантной логик.
| Классическая логика | Релевантная логика |
| (1) принцип двухзначности - высказывания принимают значения из области { t, f } | 85принцип двухзначности:{ t, f } |
| (2) принцип непротиворечия(высказывание не может иметь оба значения) | - (может иметь) |
| (3) принцип исключенного третьего (высказывание обязательно принимает значение из указанной области) | - |
| (4) принцип тождества:в сложном высказывании, системе высказываний, аргументации одно и то же высказывание принимает одно и то же значение из области { t, f } | - |
| (5) принцип матричности (функциональности) | принцип матричности |
Какова информация высказывания  в семантике обобщенных описаний состояний?
в семантике обобщенных описаний состояний?  есть
есть  М есть
М есть  Таким образом,
Таким образом,  есть
есть  и есть
и есть 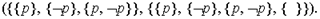 Этот логический закон (как и другие логические законы) информативен, т.е. не является тавтологией.
Этот логический закон (как и другие логические законы) информативен, т.е. не является тавтологией.
Следует ли из противоречия любое высказывание? Например, верно ли 
 Рассмотрим описание состояния
Рассмотрим описание состояния 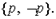 В этом описании состояния формула
В этом описании состояния формула  истинна. В самом деле:
истинна. В самом деле: 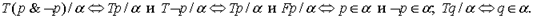 Отсюда,
Отсюда, 
Формализацией построенной семантическим методом логики является исчисление  (first degree enteilment). Определение:
(first degree enteilment). Определение: 
Схемы аксиом:

Правила вывода:

| 
|

| 
|
A, В, С - формулы языка классической логики высказываний, содержащие символы 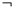 , и
, и  и не содержащие знака «
и не содержащие знака « ».
».
Обоснование первого правила вывода: если  и
и  то
то  Конъюнкция и дизъюнкция интерпретируются, соответственно, как пресечение и объединение соответствующих множеств. Поэтому
Конъюнкция и дизъюнкция интерпретируются, соответственно, как пресечение и объединение соответствующих множеств. Поэтому  так как
так как  так как
так как  Обоснование схем аксиом 6 и 7:
Обоснование схем аксиом 6 и 7:
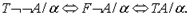
Правомерность правила контрапозиции доказана Шрамко Я.В. 
 2018-01-21
2018-01-21 880
880








