- Приведите примеры дискретных и непрерывных случайных величин.
- Что называют законом распределения вероятностей дискретной случайной величины.
- Дайте определение математического ожидания дискретной случайной величины и докажите его свойства.
- Дайте определение дисперсии дискретной случайной величины и докажите ее свойства.
- В чем состоит преимущество среднего квадратического отклонения перед дисперсией.
- Чему равны математическое ожидание и дисперсия среднего арифметического одинаково распределенных независимых случайных величин.
- Дайте определение интегральной функции и докажите ее свойства.
- Как, зная интегральную функцию, найти вероятность того, что случайная величина примет значение, заключенное в данном интервале.
- В чем состоит различие графиков интегральной функции непрерывной и дискретной случайных величин.
- Дайте определение дифференциальной функции и докажите ее свойства.
- Как, зная дифференциальную функцию, найти вероятность того, что непрерывная случайная величина примет значение, заключенное в данном интервале.
- Как найти интегральную функцию по известной дифференциальной функции.
- Дайте определение математического ожидания и дисперсии непрерывной случайной величины.
Задания:
- Найти математическое ожидание и дисперсию случайной величины y=ax+в, если закон распределения случайной величины Х задан табл чно (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).
- Даны законы распределения двух случайных величин X и Y. Найти математическое ожидание, дисперсию суммы X+Y двумя способами: 1) составив закон распределения X+Y; 2) пользуясь свойствами M(X+Y) = M(X)+M(Y), Д(Х+Y) = Д(Х)+Д(Y).
- Найти закон распределения дискретной случайной величины Х, которая может принимать только два значения: Х1 и Х2, причем Х1 < Х2, известны вероятность Р1 возможного значения Х1, математическое ожидание М(Х) и дисперсия Д(Х).
- Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины Х, заданной интегральной функцией распределения F(Х). Построить графики интегральной и дифференциальной функций.
- Случайная величина Х задана дифференциальной функцией f(х). Требуется найти интегральную функцию F(X) и
 .
.
Вариант 1.
1.
| xi | ||||
| pi | 0,4 | 0,3 | 0,1 | 0,2 |
а=2; в=2
2.
| X | Y | ||||||||
| P(X) | 0,2 | 0,3 | 0,4 | 0,1 | P(Y) | 0,6 | 0,1 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,1 | 3,9 | 0,09 |
4.

5.

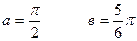
Вариант 2.
1.
| xi | ||||
| pi | 0,1 | 0,2 | 0,5 | 0,2 |
а=3; в=2
2.
| X | Y | ||||||||
| P(X) | 0,3 | 0,2 | 0,1 | 0,4 | P(Y) | 0,1 | 0,4 | 0,2 | 0,3 |
3.
| P1 | M(X) | Д(X) |
| 0,3 | 3,7 | 0,21 |
4.

5.


Вариант 3.
1.
| xi | ||||
| pi | 0,2 | 0,2 | 0,3 | 0,3 |
а=3; в=1
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,1 | 0,1 | 0,3 | P(Y) | 0,6 | 0,1 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,5 | 3,5 | 0,25 |
4.

5.


Вариант 4.
1.
| xi | ||||
| pi | 0,5 | 0,3 | 0,1 | 0,1 |
а=3; в=3
2.
| X | Y | ||||||||
| P(X) | 0,1 | 0,5 | 0,3 | 0,1 | P(Y) | 0,1 | 0,6 | 0,1 | 0,2 |
3.
| P1 | M(X) | Д(X) |
| 0,7 | 3,3 | 0,21 |
4.

5.


Вариант 5.
1.
| xi | ||||
| pi | 0,3 | 0,2 | 0,1 | 0,4 |
а=4; в=2
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,1 | 0,1 | 0,3 | P(Y) | 0,6 | 0,1 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,9 | 3,1 | 0,09 |
4.

5.
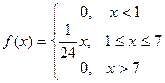

Вариант 6.
1.
| xi | ||||
| pi | 0,3 | 0,1 | 0,2 | 0,4 |
а=4; в=3
2.
| X | Y | ||||||||
| P(X) | 0,2 | 0,3 | 0,4 | 0,1 | P(Y) | 0,4 | 0,1 | 0,3 | 0,2 |
3.
| P1 | M(X) | Д(X) |
| 0,8 | 3,2 | 0,16 |
4.

5.


Вариант 7.
1.
| xi | ||||
| pi | 0,1 | 0,1 | 0,5 | 0,3 |
а=5; в=3
2.
| X | Y | ||||||||
| P(X) | 0,1 | 0,5 | 0,3 | 0,1 | P(Y) | 0,1 | 0,6 | 0,1 | 0,2 |
3.
| P1 | M(X) | Д(X) |
| 0,6 | 3,4 | 0,24 |
4.

5.


Вариант 8.
1.
| xi | 1,5 | 2,0 | 2,5 | 3,0 |
| pi | 0,5 | 0,2 | 0,2 | 0,1 |
а=2; в=4
2.
| X | Y | ||||||||
| P(X) | 0,3 | 0,2 | 0,1 | 0,4 | P(Y) | 0,1 | 0,4 | 0,2 | 0,3 |
3.
| P1 | M(X) | Д(X) |
| 0,4 | 3,6 | 0,24 |
4.

5.


Вариант 9.
1.
| xi | 1,2 | 1,4 | 1,6 | 1,8 |
| pi | 0,4 | 0,3 | 0,2 | 0,1 |
а=2; в=4
2.
| X | Y | ||||||||
| P(X) | 0,1 | 0,1 | 0,1 | 0,7 | P(Y) | 0,7 | 0,1 | 0,1 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,2 | 3,8 | 0,16 |
4.

5.


Вариант 10.
1.
| xi | 2,6 | 2,7 | 2,8 | 2,9 |
| pi | 0,5 | 0,3 | 0,1 | 0,1 |
а=2; в=5
2.
| X | Y | ||||||||
| P(X) | 0,2 | 0,3 | 0,2 | 0,3 | P(Y) | 0,3 | 0,2 | 0,3 | 0,2 |
3.
| P1 | M(X) | Д(X) |
| 0,9 | 2,2 | 0,36 |
4.

5.


Вариант 11.
1.
| xi | ||||
| pi | 0,6 | 0,2 | 0,1 | 0,1 |
а=2; в=2
2.
| X | Y | ||||||||
| P(X) | 0,2 | 0,6 | 0,1 | 0,1 | P(Y) | 0,6 | 0,2 | 0,1 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,3 | 5,4 | 0,84 |
4.

5.


Вариант 12.
1.
| xi | ||||
| pi | 0,3 | 0,1 | 0,3 | 0,3 |
а=3; в=1
2.
| X | Y | ||||||||
| P(X) | 0,2 | 0,3 | 0,2 | 0,3 | P(Y) | 0,3 | 0,2 | 0,3 | 0,2 |
3.
| P1 | M(X) | Д(X) |
| 0,9 | 2,8 | 5,76 |
4.

5.

а=1 в=3
Вариант 13.
1.
| xi | ||||
| pi | 0,3 | 0,2 | 0,2 | 0,3 |
а=4; в=5
2.
| X | Y | ||||||||
| P(X) | 0,7 | 0,1 | 0,1 | 0,1 | P(Y) | 0,5 | 0,2 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,2 | 2,6 | 0,64 |
4.
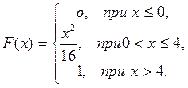
5.

а=1 в=4
Вариант 14.
1.
| xi | ||||
| pi | 0,2 | 0,4 | 0,5 | 0,1 |
а=3; в=2
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,3 | 0,1 | 0,1 | P(Y) | 0,7 | 0,1 | 0,1 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,3 | 3,1 | 1,89 |
4.

5.

а=1 в=3
Вариант 15.
1.
| xi | ||||
| pi | 0,3 | 0,3 | 0,3 | 0,1 |
а=4; в=3
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,3 | 0,1 | 0,1 | P(Y) | 0,7 | 0,1 | 0,1 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,1 | 1,9 | 0,09 |
4.
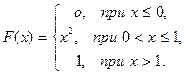
5.

а=0 в=5
Вариант 16.
1.
| xi | ||||
| pi | 0,6 | 0,2 | 0,1 | 0,1 |
а=2; в=5
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,3 | 0,1 | 0,1 | P(Y) | 0,2 | 0,6 | 0,1 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,8 | 3,4 | 0,64 |
4.

5.

а= 
Вариант 17.
1.
| xi | ||||
| pi | 0,4 | 0,4 | 0,1 | 0,1 |
а=4; в=3
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,3 | 0,1 | 0,1 | P(Y) | 0,2 | 0,2 | 0,2 | 0,4 |
3.
| P1 | M(X) | Д(X) |
| 0,7 | 3,3 | 0,21 |
4.

5.

а=0 в=3
Вариант 18.
1.
| xi | ||||
| pi | 0,1 | 0,1 | 0,7 | 0,1 |
а=2; в=4
2.
| X | Y | ||||||||
| P(X) | 0,4 | 0,1 | 0,1 | 0,4 | P(Y) | 0,3 | 0,3 | 0,3 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,4 | 2,6 | 0,24 |
4.

5.

а=0 в=2
Вариант 19.
1.
| xi | ||||
| pi | 0,1 | 0,3 | 0,3 | 0,3 |
а=2; в=2
2.
| X | Y | ||||||||
| P(X) | 0,6 | 0,1 | 0,1 | 0,2 | P(Y) | 0,5 | 0,1 | 0,1 | 0,3 |
3.
| P1 | M(X) | Д(X) |
| 0,6 | 3,2 | 2,16 |
4.

5.


Вариант 20.
1.
| xi | ||||
| pi | 0,5 | 0,3 | 0,1 | 0,1 |
а=3; в=1
2.
| X | Y | ||||||||
| P(X) | 0,4 | 0,4 | 0,1 | 0,1 | P(Y) | 0,2 | 0,6 | 0,1 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,5 | 3,5 | 0,25 |
4.

5.


Вариант 21.
1.
| xi | ||||
| pi | 0,5 | 0,1 | 0,3 | 0,1 |
а=4; в=2
2.
| X | Y | ||||||||
| P(X) | 0,3 | 0,1 | 0,4 | 0,2 | P(Y) | 0,4 | 0,3 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,6 | 3,4 | 0,24 |
4.

5.

a=-3, в=0
Вариант 22.
1.
| xi | ||||
| pi | 0,4 | 0,1 | 0,1 | 0,4 |
а=4; в=2
2.
| X | Y | ||||||||
| P(X) | 0,1 | 0,7 | 0,1 | 0,1 | P(Y) | 0,1 | 0,1 | 0,7 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,7 | 3,8 | 7,56 |
4.

5.

a=-2, в=2
Вариант 23.
1.
| xi | ||||
| pi | 0,5 | 0,1 | 0,1 | 0,3 |
а=4; в=3
2.
| X | Y | ||||||||
| P(X) | 0,2 | 0,2 | 0,2 | 0,4 | P(Y) | 0,3 | 0,4 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,4 | 4,4 | 3,84 |
4.

5.

a= 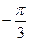 , в=0
, в=0
Вариант 24.
1.
| xi | ||||
| pi | 0,2 | 0,2 | 0,2 | 0,4 |
а=2; в=4
2.
| X | Y | ||||||||
| P(X) | 0,7 | 0,1 | 0,1 | 0,1 | P(Y) | 0,3 | 0,4 | 0,2 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,2 | 5,8 | 5,76 |
4.
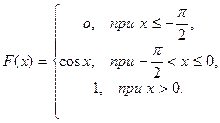
5.

a=-3, в=2
Вариант 25.
1.
| xi | ||||
| pi | 0,3 | 0,2 | 0,3 | 0,2 |
а=2; в=5
2.
| X | Y | ||||||||
| P(X) | 0,5 | 0,3 | 0,1 | 0,1 | P(Y) | 0,2 | 0,4 | 0,3 | 0,1 |
3.
| P1 | M(X) | Д(X) |
| 0,1 | 3,3 | 0,09 |
4.

5.

a=-3, в=2 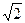 .
.
Типовой расчет №8
 2017-11-01
2017-11-01 1100
1100