2017-11-01
1789
Пусть на плоскости xy дана некоторая кривая.
Уравнение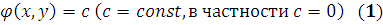 
называется уравнением кривой в неявной форме, если ему удовлетворяют координаты x, y любой точки этой кривой и, наоборот, любая пара чисел, удовлетворяющая уравнению (1), представляет собой координаты определённой точки кривой.
В аналитической геометрии часто рассматриваются две задачи:
1) по заданному геометрическому свойству кривой составить её уравнение,
2) по данному уравнению кривой выяснить её свойства и форму.
Пример. Составить каноническое уравнение гиперболы, т.е. геометрического места точек плоскости xy, разность расстояний которых от двух данных точек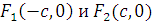 
, называемых фокусами, постоянна и равна 2a. Показать, что уравнение приводится к виду
.
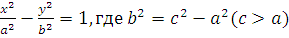Гипербола имеет следующую форму:
При a=b гипербола называется равносторонней. При повороте равносторонней гиперболы на 45˚ против часовой стрелки получим «школьную» гиперболу.
Упражнение 2. Составить уравнение геометрического места точек, отношение расстояний которых от двух данных точек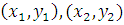 
постоянно и равно λ. Что представляет собой это множество?
Упражнение 3. Составить каноническое уравнение параболы, т.е. геометрического места точек плоскости xy, равноудалённых от точки F(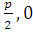 
), называемой фокусом, и прямой 
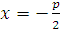, называемой директрисой.
Показать, что уравнение имеет вид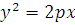 
.
Упражнение 4. Составить каноническое уравнение эллипса, т.е. геометрического места точек плоскости xy, сумма расстояний которых от двух данных точек 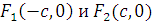, называемых фокусами, постоянна и равна 2а. Показать, что уравнение приводится к виду
.
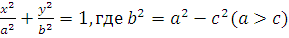Эллипс имеет следующую форму:
При a=b эллипс вырождается в окружность.
