Параметрические уравнения кривой

Представим, что точка A движется по кривой. Пусть в момент времени t её координаты

Уравнения этой системы, задающие координаты произвольной точки кривой как функции параметра t, называют уравнениями кривой в параметрической форме. Параметр t - не обязательно время, а может быть любой величиной, характеризующей положение точки на кривой.

Для канонической окружности составим уравнения в параметрической форме. Пусть радиус окружности равен R, а центр – в начале координат. Положение точки A на окружности будем характеризовать углом t, который образует радиус OA с положительной осью x. Координаты точки А: 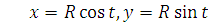Получили параметрические уравнения окружности, где параметром служит угол

Для кривой с параметрическими уравнениями (1) иногда можно получить явное уравнение. Для этого ищут параметр t из первого уравнения и подставляют во второе:

У окружности нет явного однозначного уравнения. Найдём неявное уравнение окружности, заданной параметрическими уравнениями (2):

Получили знакомое уравнение.

Упражнение 5. Составить параметрические уравнения циклоиды, т.е. кривой, которую описывает точка А окружности радиуса R, катящейся по оси : где t – угол поворота окружности, отсчитываемый от начального положения, в котором точка А совпадает с началом координат.

Упражнение 6. Показать, что эллипс допускает параметрическое задание Найти смысл параметра t.

Упражнение 7. Показать, что гипербола допускает параметрическое задание .

Почитать о гиперболических функциях и найти смысл параметра t.