В математическом анализе мы будем работать с переменными величинами. Переменная величина считается заданной, если известно множество всех значений, которые она принимает.
О.1.1. Множество действительных чисел R, дополненное элементами 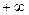 и
и 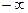 , исходя из условия, что для
, исходя из условия, что для 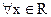 :
: 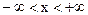 , называется расширенным множеством действительных чисел или расширенной числовой прямой. Обозначение:
, называется расширенным множеством действительных чисел или расширенной числовой прямой. Обозначение: 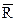 .
.
Символы 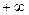 и
и 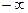 - не числа: это символическое обозначение процесса неограниченного удаления точек числовой прямой от начала О.
- не числа: это символическое обозначение процесса неограниченного удаления точек числовой прямой от начала О.
Основные подмножества (промежутки) расширенной числовой прямой
Пусть 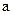 ,
, 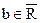 и
и 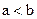 .
.
- Отрезок (сегмент, замкнутый интервал):
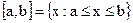 .
. - Интервал (открытый интервал):
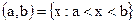 .
. - Полуинтервалы:
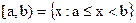 ;
; 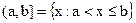 .
. - Бесконечные полуинтервалы:
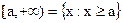 ;
; 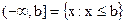 .
. - Бесконечные интервалы:
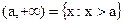 ;
; 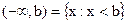 ;
;
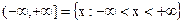 .
.
Окрестность точки
Пусть 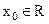 - любая точка на числовой прямой.
- любая точка на числовой прямой.
О.1.2. Окрестностью точки 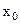 называется любой интервал
называется любой интервал 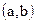 , содержащий точку
, содержащий точку 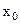 . В частности, для любого
. В частности, для любого 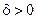 интервал
интервал 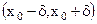 называется d-окрестностью точки
называется d-окрестностью точки 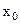 . Число
. Число 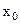 называется центром, а число
называется центром, а число 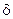 - радиусом окрестности.
- радиусом окрестности.
Обозначение: 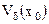 - d-окрестность точки
- d-окрестность точки 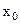 ;
; 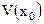 - окрестность точки
- окрестность точки 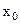 .
.
|
|
|
Таким образом, 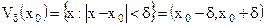 .
.
О.2.5. 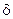 -окрестность точки
-окрестность точки 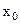 называется проколотой, если она не содержит саму точку
называется проколотой, если она не содержит саму точку 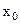 .
.
Обозначение: 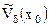 .
.
Таким образом, 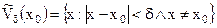 =
= 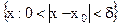 .
.
 2017-11-01
2017-11-01 1452
1452








