Вопрос 4. Сложная и обратная функции

Обратная функция

Пусть функция y = f(x) определена на множестве Х и имеет множество значений У.

О.4.1. Если каждому значению 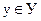соответствует единственное значение 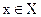, то определена функция 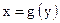с областью определения У и множеством значений Х. Такая функция 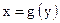называется обратной к функции y = f(x).

Про функции y = f(x) и 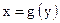говорят, что они являются взаимно обратными.

Если использовать стандартные обозначения, то обратную функцию можно записать в виде

.

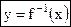Пример 5. Функци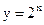и и 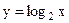являются взаимно обратными.

Графики взаимно обратных функций y = f(x) и 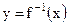симметричны относительно биссектрисы I и III координатных углов.

Сложная функция (суперпозиция функций)

Пусть даны функции:

1) 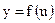с областью определения U и множеством значений У;

2) 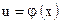с областью определения Х и множеством значений 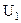, причем .

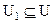О.4.2. Функция 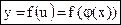, заданная на множестве Х, называется сложной функцией от х или суперпозицией функци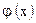й и 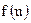. Переменная 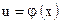называется промежуточным аргументом сложной функции.

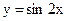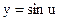Пример 6. Þ и .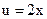

Сложная функция может иметь несколько промежуточных аргументов.

Вопрос 5. Основные элементарные функции

Наиболее простые приложения математического анализа ограничиваются кругом так называемых элементарных функций.