Взаимное расположение прямой и плоскости в пространстве

Пусть =(A; B; C) – нормальный вектор плоскости , ={ m; n; p } – направляющий вектор прямой l. Поскольку под углом между прямой и плоскостью понимают угол между этой прямой 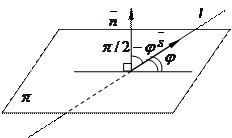и ее проекцией на эту плоскость, а вектор нормали перпендикулярен плоскости, а значит, и любой прямой, лежащей в этой плоскости, то сумма угла между векторами и и угла между прямой и плоскостью 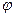составляет . Тогда по свойствам скалярного произведения векторов и формулам приведения угол между прямой и плоскостью определяется как .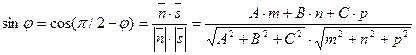

Если прямая l и плоскость перпендикулярны, то направляющий вектор прямой ={ m; n; p } и нормальный вектор плоскости =(A; B; C) параллельны, следовательно, их координаты пропорциональны. Тогда условие перпендикулярности прямой и плоскости имеет вид .

Если прямая l и плоскость параллельны, то направляющий вектор прямой ={ m; n; p } и нормальный вектор плоскости =(A; B; C) перпендикулярны, следовательно, их скалярное произведение равно нулю. Тогда условие параллельности прямой и плоскости имеет вид .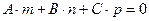

Точка пересечения прямой 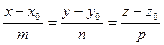и плоскости может быть найдена путем решения системы 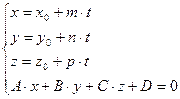. Если система имеет единственное решение, то прямая и плоскость пересекаются. Если система не имеет решения, то прямая и плоскость параллельны. Если система имеет бесконечное множество решений, то прямая лежит в плоскости.