Направляющие косинусы прямой

Направляющими косинусами прямой называют направляющие косинусы ее направляющего вектора ={ m; n; p }, которые имеют вид , , .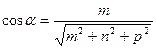

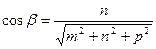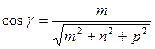Угол между прямыми в пространстве

Угол между прямыми в пространстве 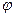определяется как угол между их направляющими векторами, если он острый, и как 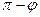, если он тупой. Если 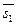={ m ₁; n ₁; p ₁} и 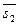={ m ₂; n ₂; p ₂} – направляющие векторы прямых, то угол между ними по свойствам скалярного произведения векторов определяется как .

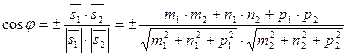Условием параллельности двух прямых является пропорциональность координат их направляющих векторов 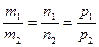, а условием их перпендикулярности .

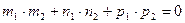Две прямые 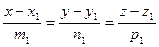и 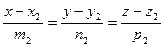лежат в одной плоскости, если

.

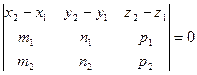В противном случае прямые скрещиваются