Условия параллельности и перпендикулярности плоскостей

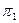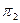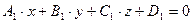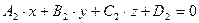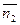Пусть две плоскости и заданы своими общими уравнениями и . Их нормальные вектора определяются как =(A ₁; B ₁; C ₁) и =(A ₂; B ₂; C ₂).

Две плоскости параллельны, если параллельны их нормальные вектора. В этом случае их координаты пропорциональны, т.е. .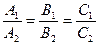

Две плоскости перпендикулярны, если перпендикулярны их нормальные вектора. В этом случае их скалярное произведение равно нулю, т.е. .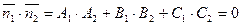

Угол между плоскостями

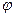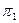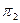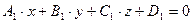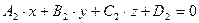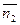Под углом между плоскостями и , заданными своими общими уравнениями и , понимают угол между их нормальными векторами =(A ₁; B ₁; C ₁) и =(A ₂; B ₂; C ₂). Тогда .

Расстояние от точки до плоскости

Пусть плоскость задана своим общим уравнением , M ₀(x ₀; y ₀; z ₀) – произвольная точка пространства Oxyz. Тогда расстояние от точки M ₀ до плоскости определяется по формуле .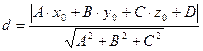

Уравнения прямой в пространстве

Линия в пространстве может быть определена либо уравнением F (x, y, z)=0, которому удовлетворяют координаты всех точек этой линии, и не удовлетворяют координаты всех точек вне этой линии, либо как линия пересечение двух поверхностей, каждая из которых задана своим уравнением.