2017-10-25
1437
|
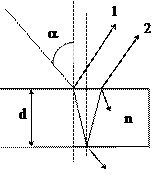
Интерференция при отражении от тонких пленок. При падении света на тонкую пленку происходит отражение от обеих поверхностей пластинки. В результате возникают когерентные волны 1 и 2, которые могут интерферировать (рис. 7). При этом
, (49)
где d – толщина пленки, n – показатель преломления, a – угол падения, l0/2 – добавочная разность хода, учитывающая смену фазы на p при отражении 1-й волны от более плотной среды (пленки).
|
Кольца Ньютона – пример полос равной толщины, наблюдаемых при отражении света от соприкасающихся друг с другом плоскопараллельной стеклянной пластинки и плосковыпуклой линзы с большим радиусом кривизны (рис. 8).
Тогда радиусы темных колец Ньютона в отраженном свете 
, (50) а радиусы светлых колец Ньютона в отраженном свете
. (51)
Здесь R – радиус кривизны линзы, n – показатель преломления вещества между линзой и пластинкой.
Практическое применение интерференции.
|
|
|
1. Существуют специальные приборы — интерферометры, действие которых основано на явлении интерференции. Их назначение — точное измерение длин волн, показателей преломления, коэффициентов линейного расширения и др.
Действие всех интерферометров основано на одном и том же принципе, и интерферометры различаются лишь конструктивно
2. Используя явление интерференции, можно оценить качество обработки поверхности изделия с точностью до 10-6 см. Для этого нужно создать тонкую клиновидную прослойку воздуха между поверхностью образца и очень гладкой эталонной пластинкой. Неровности поверхности вызовут заметные искривления интерференционных полос, образующихся при отражении света от проверяемой поверхности и нижней границы эталонной пластинки.
3. Просветление оптики. Отполированная поверхность стекла отражает около 4% перпендикулярно падающего на нее света. Современные оптические приборы состоят из большого числа оптических стекол — линз, призм и т.д. Поэтому общие потери света в объективе фотоаппарата составляют около 25%, в микроскопе — 50% и т.д. В результате освещенность изображения получается малой, ухудшается также качество изображения.
Явление интерференции применяется также для улучшения качества оптических приборов (просветление оптики) и получения высокоотражающих покрытий. Прохождение света через каждую преломляющую поверхность линзы, например через границу стекло — воздух, сопровождается отражением ≈4% падающего потока (при показателе преломления стекла ≈1,5). Так как современные объективы содержат большое количество линз, то число отражений в них велико, а поэтому велики и потери светового потока.
|
|
|
Интерференция (физика) — взаимное увеличение или уменьшение результирующей амплитуды двух или нескольких когерентных волн при их наложении друг на друга.
Дифракция света. Принцип Гюйгенса – Френеля. Зоны Френеля. Дифракция Френеля на малом круглом отверстии. Дифракция Фраунгофера на одной щели. Дифракция Фраунгофера на дифракционной решетке. Дисперсия и разрешающая способность дифракционной решетки.
Дифракцией называется огибание волной препятствий. Дифракция выражена достаточно сильно, если длина волны соизмерима с размерами препятствия. Возникновение дифракции можно объяснить с помощью принципа Гюйгенса: каждая точка, до которой доходит волновое движение, служит центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент. Для количественной оценки результатов дифракции и нахождения амплитуды результирующей волны в любой точке пространства Френель дополнил принцип Гюйгенса представлением о когерентности вторичных волн и их интерференции.
Различают: 1) дифракцию плоской волны – дифракцию Фраунгофера и 2) дифракцию сферической волны – дифракцию Френеля
Принцип Гюйгенса — Френеля формулируется следующим образом:
Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.
Расчеты с использованием принципа Гюйгенса – Френеля – чрезвычайно трудная задача. Поэтому для качественной оценки результатов дифракции Френель предложил разбивать фронт волны не на бесконечное множество точечных источников, а на конечное число зон. Зонами Френеля называются участки фронта волны, построенные таким образом, что расстояние от краев каждой зоны до точки наблюдения отличаются на l/2.
|
Построение зон для сферической волны, испущенной источником S, показано на рис. 9. Колебания, приходящие в точку наблюдения P от аналогичных точек двух соседних зон, будут находиться в противофазе. Поэтому и результирующие колебания, создаваемые каждой из зон в целом, будут для соседних зон отличаться по фазе на p.
Радиус внешней границы k-ой зоны Френеля в этом случае
, (52)
где а – расстояние от источника света до фронта волны, b – расстояние от точки наблюдения до вершины фронта волны О.
Для плоской волны радиус находится как
.
Для качественной оценки результата дифракции на малом круглом отверстии достаточно найти количество зон Френеля, попавших в это отверстие. Если количество зон четное, то в точке Р будет минимум, если нечетное – максимум.
Аналогично оценивается дифракция Фраунгофера на узкой щели (рис. 10).
Открытая часть фронта волны, дошедшей до щели, разбивается на параллельные краям щели зоны Френеля шириной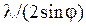 
, где j – угол дифракции. Таких зон на ширине щели укладывается 
. Если N четное, то в точке Р – минимум, если N нечетное, то в точке P – максимум. Тогда
(54)
Большое практическое значение имеет дифракция Фраунгофера на так называемой дифракционной решетке. Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же расстояние, щелей (рис. 11).
Расстояние d между серединами соседних щелей называется постоянной или периодом решетки. При этом в направлениях, для которых разность хода волн от соседних щелей равна целому числу длин волн, будут наблюдаться максимумы интенсивности, называемые главными. Таким образом, условие главных максимумов имеет вид
dsinj = 2kl/2, k = 0, 1, 2... (55)
|
|
|
При этом интенсивность главных максимумов Imax пропорциональна интенсивности Ij, создаваемой в направлении j одной щелью. Imax = N2I, (56),
где N – общее число щелей решетки.
Дифракционная решетка служит спектральным прибором, разрешающая способность которого 
(57)
где Dl – наименьшая разность длин волн двух близких спектральных линий с длинами волн l и l+Dl, при которых они еще воспринимаются раздельно (разрешаются).
Разрешающая способность дифракционной решетки может быть найдена по формуле
R = kN, (58)
где k – порядок дифракционного спектра, N – общее число щелей решетки.
