2017-11-01
583
Если u(x) и v(x)—дифференцируемые функции, то справедлива следующая формула интегрирования по частям:
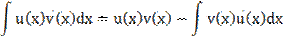
или в краткой записи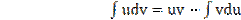 
Эта формула используется в тех случаях, когда подынтегральное выражение f(x)dx можно представить в виде udv, так что стоящий в правой части формулы интеграл при надлежащем выборе выражений u и dv может оказаться проще исходного интеграла. При этом за u удобно принимать множитель, который упрощается при дифференцировании. Например, если под знаком интеграла стоит произведение многочлена на тригонометрическую или показательную функцию, то к u следует отнести многочлен, а оставшееся выражение к dv. При этом формула интегрирования по частям может применяться неоднократно.
Следующие примеры решаются с использованием формулы интегрирования по частям.
1) 
= 
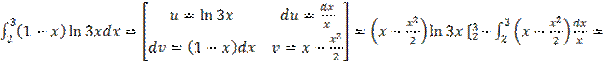
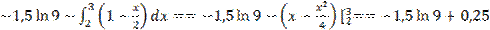
2) 
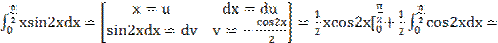
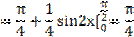
3) 
= 
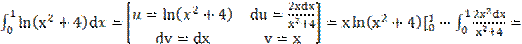
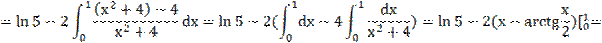
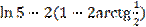
4) 
= 
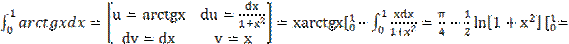
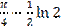
5) Вычислить определенный интеграл: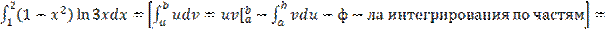 
= 
=
= 
= 
= - 
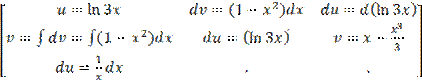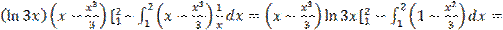
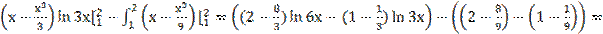
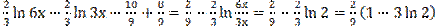
6) 
- 
= 
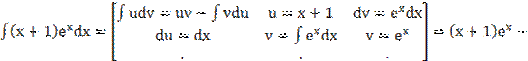
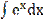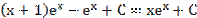
7) 
= 
- 
= 
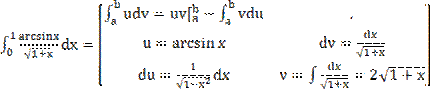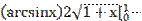
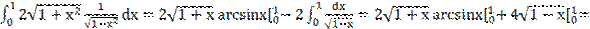
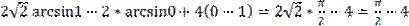
Приложение.
Вопросы к экзамену по курсу «Математический анализ» часть 1.
1. Комплексные числа. Формы записи комплексных чисел. Алгебраические операции над ними.
|
|
|
2. Множества и простейшие операции над ними. Логическая символика.
3.Функции действительной переменной, основные определения. Понятие чётности, нечётности, периодичности. Сложные функции. Обратные функции.
4. Элементарные функции и их графики, основные элементарные функции:
-степенная функция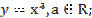 
-показательная функция y=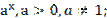 
-логарифмическая функция y=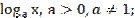 
-тригонометрические функции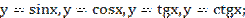 
-обратно тригонометрические функции y= arcsinx, y=arccosx, y= arctgx, y=arcctgx.
5. Явное и неявное задание функций (декартовая и полярная системы координат; параметрическое задание функций).
6. Предел последовательности (определения предела последовательности конечного и бесконечного).
7. Критерий Коши (необходимое и достаточное условия существования конечного предела последовательности).
8. Геометрический смысл бесконечного и конечного предела последовательности.
9. Ограниченная, бесконечно большая, бесконечно малая, сходящаяся, расходящаяся, монотонно возрастающая/убывающая последовательность (определения, примеры).
10. Действия над бесконечно малыми последовательностями.
11. Действия над бесконечно большими последовательностями.
12. Связь между бесконечно малыми и бесконечно большими последовательностями.
13. Основные теоремы о сходящихся последовательностях (теорема о единственности предела, теорема об ограниченности сходящейся последовательности).
14. Действия над сходящимися последовательностями.
15. Теорема о переходе к пределу в неравенствах.
16. Определение конечного предела функции в точке по Гейне, по Коши (эквивалентность определений).
|
|
|
17. Предел функций при стремлении аргумента к бесконечности, геометрический смысл.
18. Основные теоремы о пределах функций.
19. Теорема о пределе сложной функции.
20. Односторонние пределы функции.
21. Неопределённые выражения (виды неопределённостей).
22. Предел отношения многочленов при стремлении аргумента к бесконечности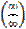 
(3-ий замечательный предел).
23. 1-ый замечательный предел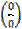 
и его следствия.
24. 2-ой замечательный предел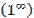 
и его следствия.
25. Вычисление пределов последовательностей и функций от рациональных и иррациональных выражений
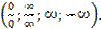
26. Сравнение функций. Порядок малости (роста).
27. Эквивалентные бесконечно малые функции.
28. Непрерывность функции в точке. Определения.
29. Односторонняя непрерывность.
30. Свойства функций, непрерывных в точке.
31. Непрерывность элементарных функций.
32. Точки разрыва и их классификации.
33. Непрерывность на отрезке и интервале. Свойства функции непрерывной на отрезке и на интервале.
34. Производная функции в точке. Односторонние производные (определения).
35. Геометрический, механический смысл производной.
36. Необходимое условие существование производной.
37. Основные правила дифференцирования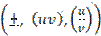 
.
38. Логарифмическое дифференцирование.
39. Производные обратных функций.
40. Производные основных элементарных функций 
41. Дифференциал функции y=f(x). Геометрический смысл. Свойства дифференциала.
42. Инвариантное свойство дифференциала.
43. Приближённые вычисления с помощью дифференциала.
44. Производные и дифференциалы высших порядков.
45. Нарушение инвариантного свойства, начиная с дифференциалов 2-ого порядка.
46. Дифференцирование функций, заданных параметрически.
47. Дифференцирование функций, заданных неявно.
48. Уравнения касательной и нормали к графику функции, заданной явно, неявно,
параметрически.
49. Теоремы о среднем (Ролля, Лагранжа, Коши). Формулировки, геометрический смысл,
следствия.
50. Правило Лопиталя (раскрытие неопределённостей вида 
и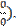 
51. Раскрытие неопределённостей вида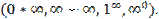 
52. Формула Тейлора n-ого порядка.
53. Формула Маклорена n-ого порядка для функций вида: sinx; cosx;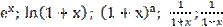 
54. Возрастание и убывание функции (определение; необходимое и достаточное условия возрастания (убывания) функции на некотором промежутке).
55. Правило исследования дифференцируемых функций на возрастание и убывание.
56. Безусловный экстремум функции y=f(x). Определения.
57. Необходимое условие экстремума дифференцируемой функции.
58. Достаточное условие существования экстремума (по первой производной).
59. Достаточные условия существования экстремума функции через производные высших
порядков.
60. Наибольшее/наименьшее значение функции на отрезке.
61. Выпуклость и вогнутость графика функции. Необходимые и достаточные условия
выпуклости и вогнутости графика функций.
62. Точки перегиба графика функции. Определение. Необходимое условие существования
точек перегиба графика функции y=f(x).
63. Достаточное условие существования точки перегиба графика функции (по 2-ой
производной; по высшим производным).
64. Асимптоты плоских кривых. Определение. Виды асимптот. Необходимые и достаточные
условия существования асимптот: вертикальных, горизонтальных, наклонных.
65. Первообразная функции. Необходимое и достаточное условия существования
первообразной. Теорема о первообразных одной и той же функции.
66. Неопределённый интеграл. Определение. Основные свойства.
67. Необходимое и достаточное условие существования неопределённого интеграла.
68. Таблица простейших неопределённых интегралов.
69. Методы интегрирования: подстановки (введения новой переменной); интегрирование по
частям).
70. Интегрирование рациональных дробей.
|
|
|
71. Интегрирование тригонометрических функций.
72. Интегрирование некоторых иррациональных функций.
73. Определённый интеграл. Определение, геометрический смысл.
74. Условия существования определённого интеграла (необходимое и достаточное условия).
75. Свойства определённого интеграла.
76. Определённый интеграл с переменным верхним пределом.
77. Формула Ньютона-Лейбница.
78. Замена переменной в определённом интеграле.
79. Формула интегрирования по частям в определённом интеграле.
80. Геометрические приложения определённого интеграла: площади плоских фигур, объём
тела, длина дуги кривой, площадь поверхности вращения.
