Основные теоремы о пределах

1.

2.

3.

4.

5.

6.

! Все правила имеют смысл, если пределы функци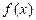й и существуют.

Используются также следующие пределы:

(первый замечательный предел);

 

(второй замечательный предел).

 

Техника вычисления пределов

При вычислении предела элементарной функции f(x) приходится сталкиваться с двумя существенно различными типами примеров.

· Функция f(x) определена в предельной точке x = a. Тогда

^.

· Функция f(x) в предельной точке x = a не определена или же вычисляется предел функции при x→∞. Тогда вычисление предела требует в каждом случае индивидуального подхода.

Необходимо помнить, что

^{, , , , , .}

Более сложными случаями нахождения предела являются такие, когда функция f(x) в точке x = a или при x→∞ представляет собой неопределенность (типа , , , , , , ).

При вычислении пределов при основные теоремы о пределах сохраняют силу и, кроме того, используются правила:

а) чтобы раскрыть неопределенность типа , необходимо числитель и знаменатель дроби разделить на наибольшую степень переменной;

б) чтобы раскрыть неопределенность типа , необходимо числитель и знаменатель дроби разделить на наименьшую степень переменной;

в) чтобы раскрыть неопределенность типа , иногда достаточно числить и знаменатель дроби разложить на множители и затем сократить дробь на множитель, приводящий к неопределенности;

г) чтобы раскрыть неопределенность типа , зависящую от иррациональности, достаточно перевести иррациональность из числителя в знаменатель или из знаменателя в числитель и сократить на множитель, приводящий к неопределенности;

д) чтобы раскрыть неопределенность типа , необходимо числитель и знаменатель дроби одновременно умножить на сопряженное выражение и тем самым свести к неопределенности вида или .

Вычислить пределы функций:

Пример 1:

Пример 2:

Пример 3:

=

Пример 4:

Пример5:

 

Пример 6:

Пример 7:

. Теорему о пределе частного здесь применить нельзя, так как числитель и знаменатель дроби конечного предела не имеют. В данном случае имеем неопределённость вида . Разделим числитель и знаменатель дроби на высшую степень х (в данном случае на х²), а затем воспользуемся теоремами о пределах функций:

.

Здесь мы воспользовались следующим равенством: (а – любое число).

Пример 8:

Пример 9:

Пример 10:

Вопросы для самопроверки по теме 1 Теория пределов:

1. Что называется функцией?

2. Что такое область определения и область значений функции

3. Перечислите способы задания функций, их достоинства.

4. Перечислите основные свойства функций.

5. Дайте определение предела функции в точке.

6. Какая функция называется непрерывной в точке?

7. Сформулируйте основные свойства пределов.

8. Как раскрывается неопределенность вида , ?