Определение2.2: Производная второго порядка (вторая производная) от функции y=f(x) есть производная от ее первой производной: 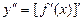 .
.
Определение 2.3: Производная третьего порядка (третья производная) от функции y=f(x) есть производная от ее второй производной:  .
.
Определение 2.4: Производная n-ого порядка (n -я производная) от функции y=f(x) есть производная от ее (n-1)-й производной:  .
.
Рассмотрим примеры.
Пример 1: Найти производную второго порядка  .
.
Решение: 





Пример2: Найти производную второго порядка функции  .
.
Решение: 

Исследование функции с помощью производной
Определение 2.5: Точка х0 называется точкой локального максимума, если для любого х из окрестности точки х0 выполняется неравенство:
 .
.
Определение 2.6: Точка х0 называется точкой локального минимума, если для любого х из окрестности точки х0 выполняется неравенство:
 .
.
Точки минимума и максимума функции называются точками экстремума данной функции, а значения функции в этих точках – экстремумами функции.
Точками экстремума могут служить только критические точки I рода, т.е. точки, принадлежащие области определения функции, в которых производная  обращается в нуль или терпит разрыв.
обращается в нуль или терпит разрыв.
Правило нахождения экстремумов функции 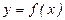
 2017-11-01
2017-11-01 461
461








