Поверхности 2-го порядка

 

Студент должен уметь распознавать указанные в таблице две поверхности 2-го порядка по их каноническим уравнениям, используя при этом метод сечений.

Таблица 2

Каноническое уравнение	Название	Схематический чертеж
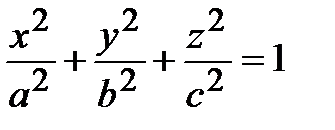	Трехосный эллипсоид
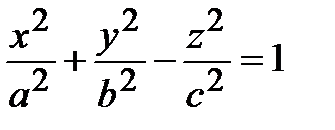	Однополостный гиперболоид
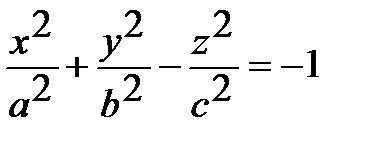	Двуполостный гиперболоид
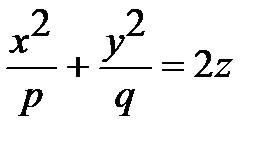	Эллиптический параболоид
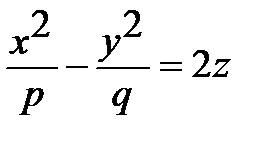	Гиперболический параболоид
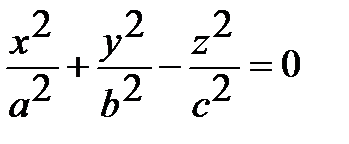	Конус 2-го порядка

Следует, также, обратить внимание на цилиндры 2-го порядка

 

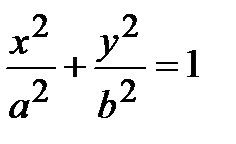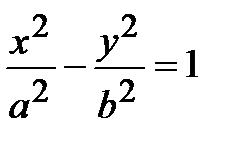; ; у ²= 2 рх

 

и на поверхности вращения 2-го порядка. Например, если в уравнении однополостного гиперболоида

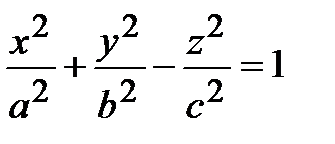
Положить а = b, то в сечении поверхности плоскостью z = h будут получаться окружности

,

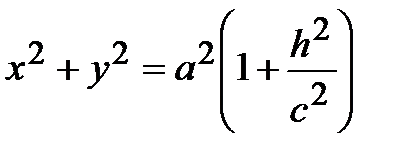следовательно, в этом случае поверхность является однополостным гиперболоидом вращения (он получается вращением гиперболы

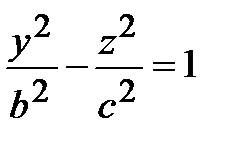вокруг оси ОZ).

 

Пример 32. Составить уравнение поверхности, образованной вращением линии x ² - pz ² = 4 вокруг оси OZ. Подобрать значение параметра р так, чтобы точка А (1,2,-1) лежала на этой поверхности. Указать название полученной поверхности и сделать её эскиз.

Решение. Уравнением вращения линии F(x,z) = 0 вокруг оси OZ является уравнение

,

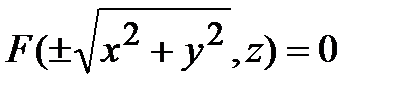так как при вращении вокруг оси OZ в уравнении без изменения остается координата z, а х заменяется на 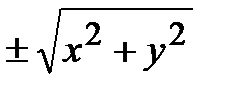(аналогичный факт имеет место и по отношению к поверхностям, получаемым вращением плоских линий вокруг других координатных осей).

Таким образом, в рассматриваемом примере получим уравнение

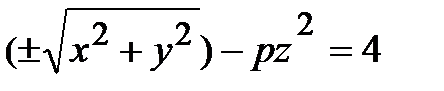или x ² + y ² – pz ² = 4.

Найдем параметр р, учитывая требования задачи. Координаты точки А должны удовлетворять найденному уравнению поверхности. Подставляя координаты точки в уравнение, получим 1+ 4 - р = 4 Þ р = 1. Тогда искомое уравнение примет вид

x ² + y ² – z ² = 4 или в канонической форме .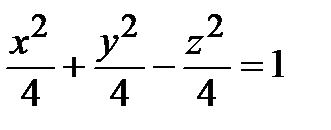

Это уравнение описывает однополостный гиперболоид вращения.

 

Пример 33. Построить поверхность, определяемую уравнением:

9 x ² + 4 y ²+ 36 z ² -18 x - 16 y +216 z + 313 = 0.

Для выполнения задания необходимо:

а) привести данное уравнение поверхности к каноническому виду;

б) определить вид поверхности и ее расположение относительно системы координат;

с) записать название поверхности и сделать чертеж.

 

Решение. Группируем члены уравнения, содержащие одинаковые переменные:

 

(9 x ² - 18 x) + (4 y ² - 16 y) + (36 z ² + 216 z) + 313=0 Þ

 

9(x ² - 2 x) + 4(y ² - 4 y) + 36(z ² + 6 z) + 313=0.

 

Выделяем полный квадрат в каждой скобке:

 

9((x ² - 2 x +1) - 1) + 4((y ²- 4 y + 4) - 4)+36((z ²+ 6 z + 9) - 9) + 313 = 0.

 

Получим 9((x -1) ²-1) + 4((y -2) ²- 4) + 36((z +3) ²-9) + 313 = 0 Þ

 

9(x -1) ²-9 + 4(y -1) ²-16 + 36(z +3) ²-324 + 313=0 Þ

 

9(x -1) ² + 4(y -2) ² + 36(z + 3) ² = 36.

 

Разделим обе части уравнения на свободный член и получим каноническое уравнение эллипсоида с центром в точке О₁(1,2,-3)

 

.

 

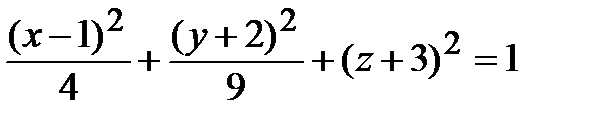Для построения этого эллипсоида сделаем в уравнении замену переменных

x -1= x ₁, y -2 = y ₁, z +3 = z ₁.

В новых переменных уравнение эллипсоида примет вид:

 

.

 

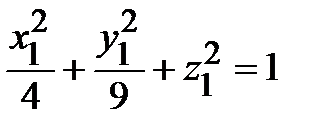Сделаем чертеж. Для этого через центр эллипсоида O₁(1,2,-3) проведем оси

O₁X₁ , O₁Y_1, O₁Z₁, и в этой системе координат построим эллипсоид

 

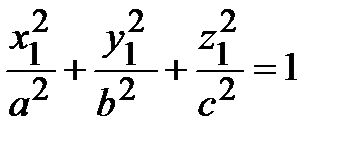, где a = 2, b = 3, c = 1 (рис. 7).

 

 

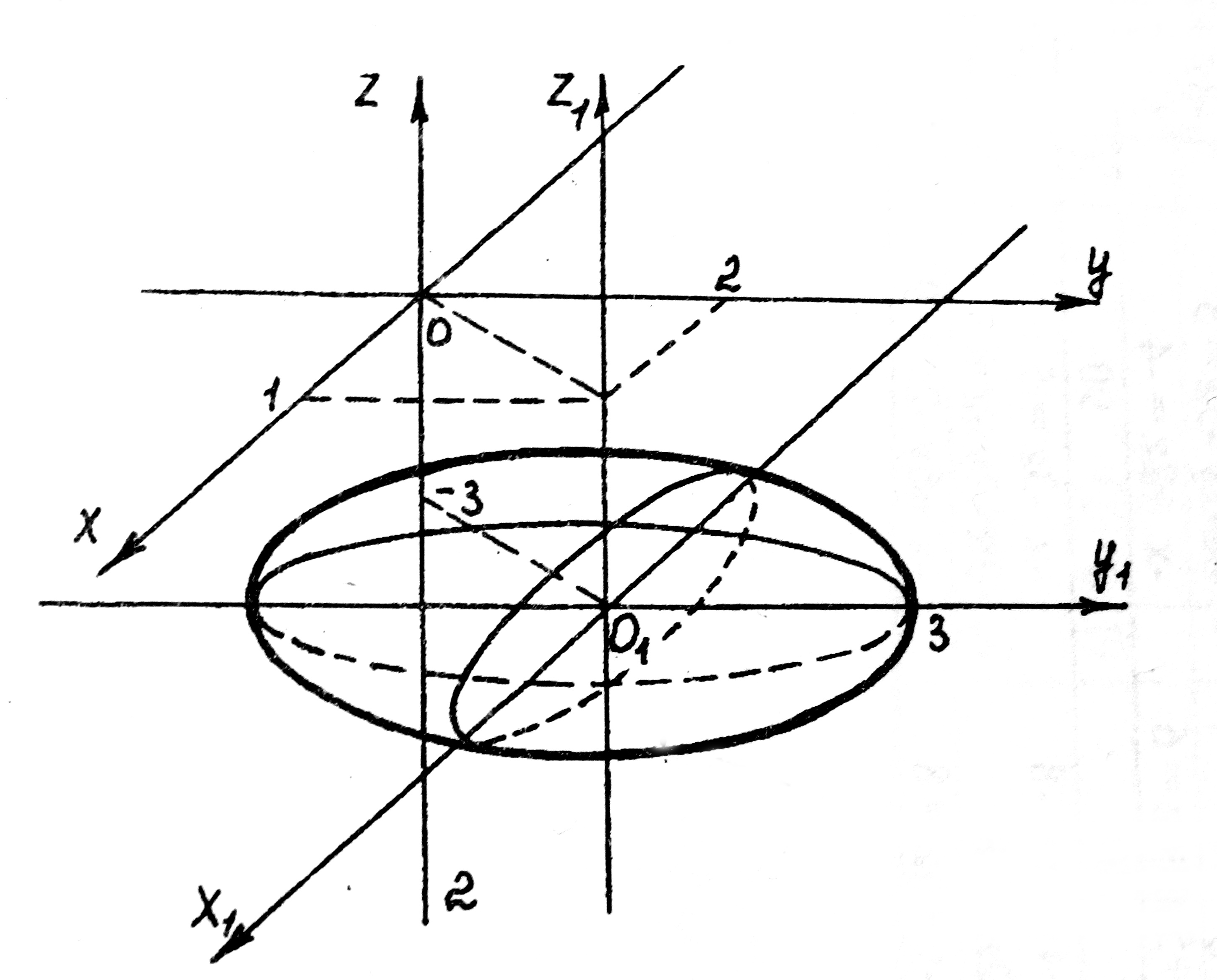
Рис. 7

 

Вопросы для самопроверки

1. Какие поверхности заданы уравнениями:

 

4 x ²+9 y ²+ z ² = 36;

4 x ²+9 y ²- z ² = 36;

4 x ²+9 y ²- z ²= -36;

3 x ²+4 y ² = z ²;

3 x ²- 4 y ²= z ²;

x ²+ y ² = z;

x ²+ z ²= 1;

x ²– z ²= 0;

y ²= 4 x.

 

2. Составить уравнение поверхности, образованной вращением прямой

у = k х вокруг оси ОХ.

 

3. Какую поверхность в пространстве описывает алгебрарическое уравнение 2-го порядка, содержащее лишь две переменные?