Пусть функция z=f(x,y) определена и непрерывна в ограниченной замкнутой области D плоскости Oxy. Разобьем область D произвольным образом на n областей S1, S2, …, Sn, в каждой из них произвольным образом выберем по точке:  ,
, 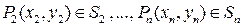 , которые назовем точками пунктуации. Обозначим через
, которые назовем точками пунктуации. Обозначим через  - площадь, а через
- площадь, а через  - расстояние между двумя наиболее удаленными точками i-ой области (диаметр i-ой области), i=1,…,n. Пусть
- расстояние между двумя наиболее удаленными точками i-ой области (диаметр i-ой области), i=1,…,n. Пусть  .
.
Определение. Интегральной суммой Римана функции z=f(x,y) по области D называется
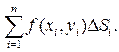 (1)
(1)
Заметим, что сумма зависит от способа разбиения области D на части и от способа выбора точек пунктуации.
Определение. Если существует предел интегральной суммы Римана (1) при  , и этот предел не зависит ни от способа разбиения области, ни от выбора точек пунктуации, то он называется двойным интегралом от функции z=f(x,y) по области D и обозначается
, и этот предел не зависит ни от способа разбиения области, ни от выбора точек пунктуации, то он называется двойным интегралом от функции z=f(x,y) по области D и обозначается

Таким образом,
 (2)
(2)
Отметим, что согласно определению  равен площади области D.
равен площади области D.
Свойства двойных интегралов аналогичны свойствам определенных интегралов. Выделим два из них, наиболее часто используемых на практике.
1) Свойство линейности. Если функции f(x,y) и g(x,y) интегрируемы в области D, то справедлива формула:

2) Свойство аддитивности. Если область D разбита на две области D1 и D2 без общих точек, и функция f(x,y) интегрируема в области D, то справедлива формула:

Теорема 1. Если область D ограничена слева и справа вертикальными прямыми x=a, x=b, а снизу и сверху – кривыми  , причем функции
, причем функции  - непрерывны и
- непрерывны и  на промежутке [a,b] (Рис.1), то
на промежутке [a,b] (Рис.1), то
 . (3)
. (3)
Таким образом, вычисление двойных интегралов сводится к последовательному вычислению двух интегралов, сначала вычисляется интеграл по переменной y (x - параметр), а потом полученный результат интегрируется по x, то есть двойной интеграл представим в виде повторных интегралов.

Рис.1.
Область D, как в теореме 1, называется правильной в направлении оси Oy.
Пример 1. Вычислить двойной интеграл:  по области D, ограниченной линиями:
по области D, ограниченной линиями: 
Решение. Согласно теореме 1 двойной интеграл 
 . Сначала вычислим интеграл по переменной y (x – параметр):
. Сначала вычислим интеграл по переменной y (x – параметр):
 .
.
Окончательно имеем
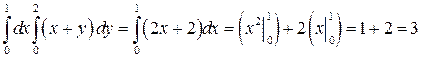 .
.
 2017-11-01
2017-11-01 3193
3193








