Требуется вычислить двойной интеграл  , от непрерывной функции
, от непрерывной функции  .
.
Предположим сперва, что область интегрирования σ ограниченна двумя непрерывными кривыми  и
и  и двумя прямыми x=a, x=b, причем для всех значений x, заключенных между a и b, имеет место неравенство
и двумя прямыми x=a, x=b, причем для всех значений x, заключенных между a и b, имеет место неравенство  .
.
Проведем через точку (x; 0) оси 0x прямую, параллельную оси 0y. эта прямая встречает кривые, ограничивающие область σ, соответственно в очках  и
и  . Точку
. Точку 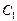 будем называть точкой входа, а точку
будем называть точкой входа, а точку  – точкой выхода. Их координаты обозначим соответственно
– точкой выхода. Их координаты обозначим соответственно 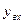 и
и 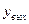 . Ордината точки выхода равна
. Ордината точки выхода равна  , а ордината точки выхода равна
, а ордината точки выхода равна  . Известно что двойной интеграл
. Известно что двойной интеграл  численно равен V цилиндрического тела, ограниченного частью поверхности
численно равен V цилиндрического тела, ограниченного частью поверхности  , которая проектируется в площадку σ (см. рис.2):
, которая проектируется в площадку σ (см. рис.2):

Рис. 2
 или
или 
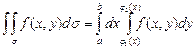 , (3)
, (3)
или  (4)
(4)
Это и есть искомая формула.
Пример 1. Вычислить двойной интеграл  , если областью интегрирования σ является треугольник, ограниченный прямыми y=0, x=2, y=
, если областью интегрирования σ является треугольник, ограниченный прямыми y=0, x=2, y=  (см. рис.3).
(см. рис.3).

|
 (x)=0,
(x)=0,  (так как точка входа лежит на оси 0x, а точка выхода - на прямой
(так как точка входа лежит на оси 0x, а точка выхода - на прямой  ); a=0, b=2.
); a=0, b=2. Поэтому, применяя формулу (3),
имеем
 .
.
Вычислим внутренний интеграл, в котором считаем x постоянным: 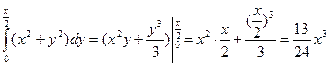 .
.
Следовательно,  .
.
Применяя для вычисления двойного интеграла  формулу (4), получим, конечно, тот же результат. Замечая, что в этом случае
формулу (4), получим, конечно, тот же результат. Замечая, что в этом случае  (так как точка входа лежит на прямой
(так как точка входа лежит на прямой  или x=2y, а точка выхода на прямой x=2), c=0, d=1, получим
или x=2y, а точка выхода на прямой x=2), c=0, d=1, получим  .
.
Так как
 ,
,
то 
 2017-11-01
2017-11-01 1477
1477








