Шашырау сипаттамалары

Медиана (median, me)

Медиана(Ме) вариациялық қатарды тең екіге бөлетін мән, одан төмен және одан жоғары мәндердің бірдей саны орналасады және медианаға дейін одан кіші мәндердің 50% - ы, одан кейін үлкен мәндердің 50% -ы жатады.

Егер бақылаулар саны n тақ болса, онда медиананы есептеу жеңіл. Бұл вариациялық қатардағы – ші нөмірлі варианта болады. Мысалы, егер n=11 болса, онда медиана 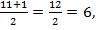вариациялық қатардағы 6–шы нөмірлі варианта болады. Егер n жұп болса, онда медиана вариациялық қатардағы 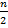- ші және 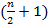– ші нөмірлі варианталардың арифметикалық ортасы болады. Мысалы, егер n= 20 болса, онда медиана 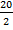= 10- шы және 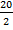+ 1=11- нөмірлі варианталардың арифметикалық ортасы болады.

Егер деректердің таралуы симметриялы болса, онда медиана орта мәнге ұқсас, егер деректердің таралуы оң жаққа қарай қисайған асимметриялы болса, онда орта мәннен кіші, егер деректердің таралуы сол жаққа қарай қисайған асимметриялы болса, онда медиана орта мәннен үлкен.

 

Мода (moda, mo)

Мода (Мо) – деректер жиынында ең жиі кездесетін мән, егер деректер үздіксіз болса, онда оларды топтастырып модальды топты анықтайды. Кейбір деректер жиынында мода болмайды, себебі әрбір мән тек бір рет кездеседі. Кейде модалар бірнешеу болуы мүмкін, ол біртекті емес жиынтықтарда кездеседі. Мода жалпылайтын сипаттама ретінде өте сирек қолданылады.

 

Полигон және гистограмма.

Көрнекілік үшін статистикалық таралудың түрлі графиктер салынады, соның ішінде полигон мен гистограмма тұрғызылады.

1. Х дискретті белгісінің таралуы.

Жиіліктер полигоны деп (х₁, n₁), (х₂, n₂),..., (х_к, n_к) нүктелерін қосатын сынық сызықты айтады жиіліктер полигонын тұрғызу үшін абциссалар осінде х_і варианталарын, ал ординаталр осінде-оларға сәйкес n_і жиіліктерді орналастырады. (х_і, n_і) нүктелерін түзудің кесінділерімен қосып, жиіліктер полигонын салады.

Салыстырмалы жиіліктер полигоны деп кесінділері (x₁,W₁), (x₂,W₂),..., (x_к,W_к), нүктелерін қосатын сынық сызықты айтады. Салыстырмалы жиіліктер полигонын тұрғызу үшін абциссалар осінде x_і варианталарын, ал ординаталар осінде оларға сәйкес W_і салыстырмалы жиіліктер полигонын тұрғызады.

1-суретте келесі салыстырмалы жиіліктер таралуының полигоны бейнеленген.

 

1-сурет

2. Х үзіліссіз белгісінің таралуы.

Статистикалық үзіліссіз қатарды (немесе таралудың эмпирикалық функциясын) әдетте таңдамада бір-бірінен өзгеше варианталар көп болмаған жағдайда немесе осы себеппе зерттеуші үшін үзіліссіздік бар болған жағдайда қолданады. Егер бізді қызықтыратын бас жиынтықтың Х белгісі үзіліссіз болса, онда варианталар интервалдарға топтастырылады.

Көлемі n таңдамадағы берілгендерді топтастырғанда барлық варианталарды қамтитын [a,b] кесіндісін k интервалдарға 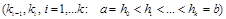бөледі. (әдетте ).

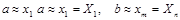Осыдан соң, әрбір интервалдың жиілігін, яғни і- ші интервалға түсетін бақылаулар санын анықтау керек. Айқындылық үшін - 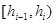жарты интервалында жататын варианталар санына тең деп ұйғарамыз. Барлық жағдайда аралық 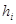- ге тең болады.k – интервалдар саны.

Ескерту. Көбіне барлық і үшін 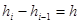, яғни топтастыру тең h қадаммен алынады. Бұл жағдайда 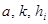табу үшін келесі ұсынысты жетекшілікке алуға болады.

1. R =X_max –X_mіn табамыз, мұндағы R – ең үлкен және ең кіші варианталардың айырымы.

2. 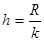k-топтар саны, h-қадам.

3. (Стерджес формуласы)

4. a=x_mіn, b=x_max

5.

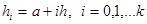
Алынған топтастыруды жиілік кестесі түрінде ұсыну қолайлы. Бұл кестені таралудың статистикалық интервалдық қатары деп атайды.

Топтастырудың интервалы			..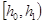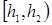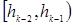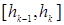
Жиіліктер			..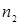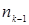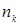

.

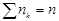Осы кестені n_і жиіліктерді салыстырмалы жиіліктермен алмастырып мынадай түрде жазуға болады:

Топтастыру интервалы			..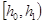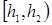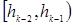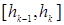
Салыстырмалы жиіліктер			..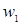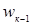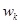

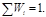
Жиіліктердің графиктік түрі - жиіліктер гистограммасы деп аталатын арнайы график болып табылады.

Жиіліктер гистограммасы деп табандары h-қа, биіктіктері 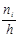(жиілік тығыздығы) қатынасына тең тіктөртбұрыштардан тұратын баспалдақты фигураны айтады.

Үзіліссіздік белгісі жағдайында гистограмма салған жөн, ол үшін белгінің барлық бақыланатын мәндер жататын интервалды ұзындығы Һ-қа тең бірнеше дербес (жеке) интервалдарға бөліп, әрбір дербес n_і интервал үшін і -ші интервалға түскен варианталар жиіліктерінің қосындысын табады. і-ші дербес төртбұрыштың ауданы 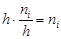- і-ші интервалға түскен варианталар жиіліктерінің қосындысына тең, сондықтан жиіліктер гистограммасының ауданы барлық жиіліктердің қосындысына тең, яғни таңдаманың көлеміне тең.

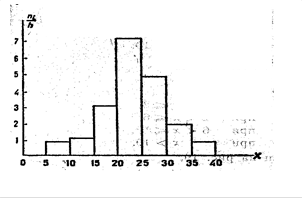
Салыстырмалы жиіліктер гистограммасы деп табандары h-қа, биіктіктері 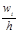(салыстырмалы жиілік тығыздығы) қатынасына тең тіктөртбұрыштардан тұратын баспалдақты фигураны айтады.

Салыстырмалы жиіліктер гистограммасын тұрғызу үшін абциссалар осінде дербес интервалдар салып, олардың үстінен абцисса осіне параллель 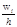қашықтықта кесінділер жүргіземіз. і -ші дербес төртбұрыштың ауданы 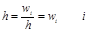- ші интервалға түскен варианталардың салыстырмалы жиіліктеріне тең. Сонымен, салыстырмалы жиіліктер гистограммасының ауданы барлық салыстырмалы жиіліктер қосындысына, яғни 1-ге тең.

1-ден 10 дейінгі сандардың ондық логарифмдері

п
lg п	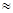	0,30	0,48	0,60	0,70	0,78	0,85	0,90	0,95

 

 

Бас орта

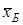бас орта деп бас жиынтық белгісінің орта арифметикалық мәнін айтады.

Егер N көлемді бас жиынтық белгісінің барлық х₁,......х_N мәндері әртүрлі болса, онда

Егер x₁, x₂,….x_к белгісінің мәндері сәйкесінше N₁, N₂, …….N_k жиіліктерге ие болса, мұнда N₁+ N₂+....+.N_k=N

;

 

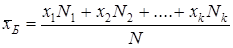Таңдама орта

Х сандық белгісіне қатысты бас жиынтықты зерттеу үшін n көлемді таңдама алынсын.

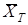таңдама орта деп таңдама жиынтық белгісінің орта арифметикалық мәнін айтады.

Егер n көлемді таңдаманың барлық x₁, x₂,….x_n мәндері әр түрлі болса, онда

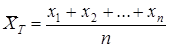
Егер таңдаманың x₁, x₂,….x_к мәндерінің сәйкесінше жиіліктері n₁, n₂,……..n_k болса, және n₁+n₂+…..+n_k=n онда 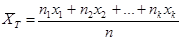, немесе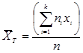

Көлемі n – ге тең Х сандық белгінің мәндер жиынтығын қарастырамыз.

Белгінің мәні	х1	х2	…	хк
Жиілік	п1	n2	…	пк

мұнда .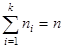

Шашырау сипаттамалары

Орта мәндер өзгермелі белгілер жөнінде толық ақпарат бермейді. Мәселен, екі таңдаманың таралуларының орта мәндері бірдей болулары мүмкін, бірақ олардың біреуінде белгілердің мәндері орта мәннің айналасына жақын орналасуы, ал екіншісінде алыс орналасулары мүмкін. Сондықтан орта мәндермен қатар таңдаманың шашырау сипаттамаларын да есептейді.

Шашырау көрсеткіштеріне таңдаманың дисперсиясы, стандарттық ауытқу, таңдаманың құлашы, процентильдер(квартильдер),вариация коэффициенті, квартильаралық құлаш жатады.

Бас дисперсия

Бас жиынтықтың Х сандық белгісі мәндерінің өз орта мәнінің маңайында шашырауын сипаттау үшін бас дисперсия сипаттамасы енгізіледі.

бас дисперсиясы деп бас жиынтық белгісі мәндерінің 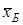орта мәнінен ауытқуының квадратының орта арифметикалық мәнін айтады.

Егер N көлемді бас жиынтық белгісінің барлық х₁, х₂ ,.., х_N мәндері әртүрлі болса, онда

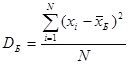
Егер белгінің барлық х₁, х₂ ,.., х_к мәндерінің сәйкес жиіліктері N₁, N₂, …, N_k бар болса, жәнеN₁+N₂+ +…+N_k=N, онда ;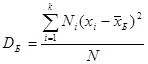

Бас жиынтықтың сандық белгісі мәндерінің өз орта мәнінің маңайында шашырауын сипаттау үшін дисперсиядан басқа Стандарттық ауытқуды пайдаланады.

Бас орташа квадраттық ауытқу деп бас дисперсиядан алынған квадрат түбірді айтады: .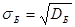

Таңдама дисперсия S деп белгінің бақыланатын мәндерінің 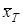орта мәнінен ауытқу квадраттарының орта арифметикалық мәнін айтады.

Егер n көлемді таңдаманың барлық x₁, x₂,….x_n белгілерінің мәндері әр түрлі болса, онда

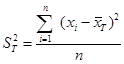
Егер x₁, x₂,….x_n мәндерінің жиіліктері бар және сәйкесінше n₁, n₂, …, n_k болса, мұндағы

n₁+ n₂+ …+ n_k=n, онда .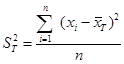

Теорема: Дисперсия таңдама мәндерінің квадраттарының орта мәні мен орта мәнінің квадратының айырымына тең: .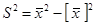

Стандарттық ауытқу (standart deviation, SD)

Стандарттық ауытқу(орта квадраттық ауытқу) деректер мәндерінің түрленгіштігін бейнелейді және оны деректер жиынының өзгергіштігін айқындау үшін қолданады. Стандарттық ауытқу – дисперсиядан алынған оң түбір.

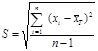
Бұл көрсеткіш неғұрлым үлкен болса, өлшенген айнымалының шашырауы соғұрлым үлкен. Стандарттық ауытқулардың өлшем бірлігі таңдама ортаның өлшем бірлігімен бірдей.

Стандарттық ауытқудың қолданылуы

Педиатрияда стандарттық ауытқуды балалардың физикалық дамуын бағалау үшін қолданады: ол нақты баланың деректерін сәйкес стандарттық көрсеткіштермен салыстыру арқылы жүзеге асады. Стандарт ретінде сау балалардың физикалық дамуларының көрсеткіштерінің орта мәні алынады. Көрсеткіштерді стандартпен салыстыруды арнайы кесте арқылы жүргізеді, кестеде стандарттар оларға сәйкес келетін сигмальді шкалалармен бірге келтіріледі.

Егер баланың физикалық дамуының көрсеткіші с тандарт ± 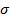ішінде болса, онда баланың физикалық дамуы (осы көрсеткіш бойынша) қалыпқа сәйкес деп саналады. Егер көрсеткіш стандарт ±2 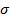ішінде жатса, онда қалыптан айтарлықтай емес (субнорма) ауытқу бар. Егер көрсеткіш бұл шекаралардан шығып кетсе, онда баланың физикалық дамуында қалыптан күрт айырмашылық бар (паталогия болуы мүмкін).