Закон всесвітнього тяжіння у скалярній формі
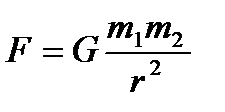 , (1.87)
, (1.87)
де 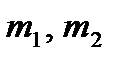 — маси матеріальних точок;
— маси матеріальних точок;  — відстань між ними;
— відстань між ними; 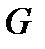 = 6,67*10-11Нм2/кг2— гравітаційна стала.
= 6,67*10-11Нм2/кг2— гравітаційна стала.
Закон всесвітнього тяжіння у векторній формі
 , (1.88)
, (1.88)
де 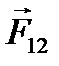 — сила, що діє на першу матеріальну точку з боку другої;
— сила, що діє на першу матеріальну точку з боку другої; 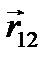 — радіус-вектор, що з’єднує другу точку з першою.
— радіус-вектор, що з’єднує другу точку з першою.
Третій закон Кеплера
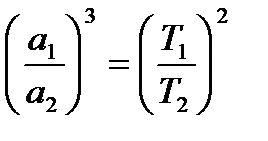 , (1.89)
, (1.89)
де  — великі півосі еліптичних орбіт планет навколо Сонця;
— великі півосі еліптичних орбіт планет навколо Сонця;  — періоди обертання цих планет.
— періоди обертання цих планет.
Напруженість гравітаційного поля тіла масою 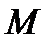
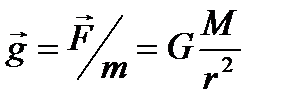 , (1.90)
, (1.90)
де 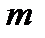 - маса пробного тіла.
- маса пробного тіла.
Потенціал гравітаційного поля в даній точці
 . (1.91)
. (1.91)
Зв’язок між напруженістю і потенціалом гравітаційного поля
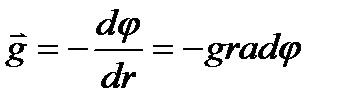 . (1.92)
. (1.92)
Основне рівняння руху матеріальної точки змінної маси (рівняння Мещерського)
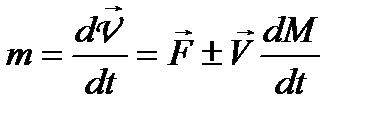 , (1.93)
, (1.93)
де 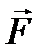 — рівнодійна зовнішніх сил, що діють на тіло змінної маси
— рівнодійна зовнішніх сил, що діють на тіло змінної маси 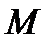 ;
;  — швидкість від'єднання (приєднання) частинок тіла (ця швидкість відраховується відносно самого тіла).
— швидкість від'єднання (приєднання) частинок тіла (ця швидкість відраховується відносно самого тіла).
Швидкість 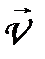 руху ракети вертикально вгору, коли дії зовнішніх сил немає, визначається за формулою Ціолковського:
руху ракети вертикально вгору, коли дії зовнішніх сил немає, визначається за формулою Ціолковського:
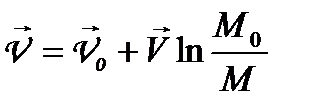 . (1.94)
. (1.94)
Якщо в початковий момент часу швидкість ракети 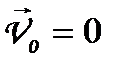 , то
, то
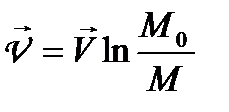 , (1.95)
, (1.95)
де 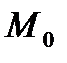 — початкова (стартова) маса ракети;
— початкова (стартова) маса ракети; 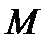 — маса ракети в даний момент часу. Якщо паливо згоряє повністю, то
— маса ракети в даний момент часу. Якщо паливо згоряє повністю, то 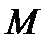 — маса конструкції ракети.
— маса конструкції ракети.
§ 7. МЕХАНІКА РІДИН 1 ГАЗІВ
Рівняння нерозривності течії стаціонарного потоку ідеальної рідини
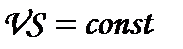 , (1.96)
, (1.96)
де 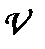 — швидкість рідини;
— швидкість рідини; 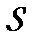 — площа поперечного перерізу трубки течії.
— площа поперечного перерізу трубки течії.
Робота сил зовнішнього тиску по переміщенню рідині об’ємом 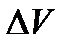
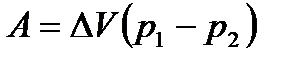 . (1.97)
. (1.97)
Рівняння Бернуллі для стаціонарного потоку ідеальної рідини
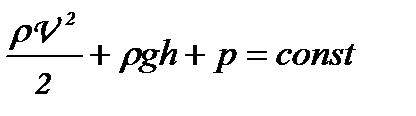 , (1.98)
, (1.98)
де 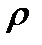 — густина рідини;
— густина рідини; 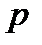 — зовнішній тиск;
— зовнішній тиск; 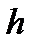 — висота перерізу трубки течії над певним рівнем.
— висота перерізу трубки течії над певним рівнем.
Швидкість витікання ідеальної рідини через малий отвір в широкій посудині (формула Торрічеллі)
 , (1.99)
, (1.99)
де 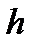 — висота стовпа рідини над отвором.
— висота стовпа рідини над отвором.
Лобовий опір тіла, що знаходиться в ламінарному потоці в'язкої рідини,
 , (1.100)
, (1.100)
де 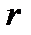 — коефіцієнт, що залежить від форми і розмірів тіла;
— коефіцієнт, що залежить від форми і розмірів тіла;  — динамічна в'язкість;
— динамічна в'язкість;
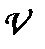 — швидкість течії.
— швидкість течії.
При русі тіла кулеподібної форми у в'язкому середовищі (або при обтіканні нерухомого тіла) сила опору описується законом Стокса:
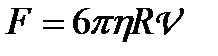 , (1.101)
, (1.101)
де 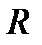 — радіус кулі.
— радіус кулі.
Розподіл швидкості ламінарної течії рідини у циліндричній трубі радіуса 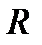
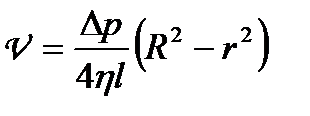 , (1.102)
, (1.102)
де 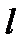 - довжина трубки;
- довжина трубки; 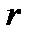 - відстань від осі трубки.
- відстань від осі трубки.
При ламінарній течії через трубку довжиною 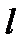 і радіуса
і радіуса 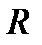 за час
за час  проходить об'єм рідини
проходить об'єм рідини 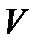 . Цей об'єм визначається за формулою Пуазейля:
. Цей об'єм визначається за формулою Пуазейля:
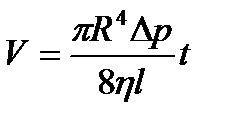 , (1.103)
, (1.103)
де 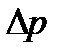 -- різниця тиску на кінцях трубки.
-- різниця тиску на кінцях трубки.
У випадку турбулентного потоку при не дуже великих швидкостях течії лобовий
опір
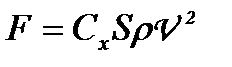 , (1.104)
, (1.104)
де 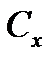 — коефіцієнт лобового опору, який залежить від форми тіла і числа Рейнольдса;
— коефіцієнт лобового опору, який залежить від форми тіла і числа Рейнольдса; 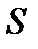 —площа міделя (площа проекції тіла на площину, перпендикулярну до швидкості потоку);
—площа міделя (площа проекції тіла на площину, перпендикулярну до швидкості потоку); 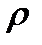 — густина середовища.
— густина середовища.
Число Рейнольдса
 , (1.105)
, (1.105)
де 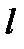 —характеристичний розмір (величина, що характеризує лінійні розміри тіла).
—характеристичний розмір (величина, що характеризує лінійні розміри тіла).
§ 8. ЕЛЕМЕНТИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ
Перетворення Лоренца:
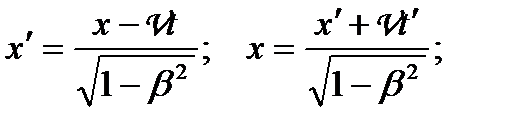 (1.106)
(1.106)
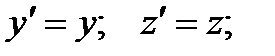 (1.107)
(1.107)
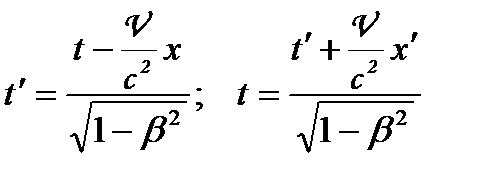 , (1.108)
, (1.108)
де 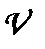 — швидкість відносного руху інерціальних систем відліку; с — швидкість світла у вакуумі;
— швидкість відносного руху інерціальних систем відліку; с — швидкість світла у вакуумі; 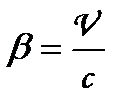 . (1.109)
. (1.109)
Тривалість події в рухомій системі відліку  , (1.110)
, (1.110)
де 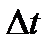 — тривалість події в нерухомій системі відліку.
— тривалість події в нерухомій системі відліку.
Скорочення довжини рухомого тіла
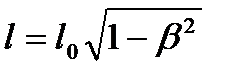 , (1.111)
, (1.111)
де 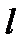 — довжина рухомого тіла;
— довжина рухомого тіла; 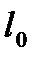 — власна довжина тіла.
— власна довжина тіла.
Релятивістський закон додавання швидкостей
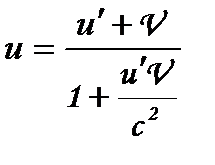 , (1.112)
, (1.112)
де 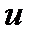 — швидкість тіла в нерухомій системі (абсолютна швидкість);
— швидкість тіла в нерухомій системі (абсолютна швидкість); 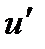 — швидкість тіла в рухомій системі (відносна швидкість).
— швидкість тіла в рухомій системі (відносна швидкість).
Релятивістська маса і імпульс такі:
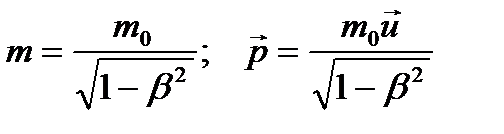 , (1.113)
, (1.113)
де 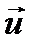 — швидкість тіла у вибраній системі відліку;
— швидкість тіла у вибраній системі відліку; 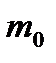 — маса тіла в нерухомому стані у вибраній системі відліку (маса спокою).
— маса тіла в нерухомому стані у вибраній системі відліку (маса спокою).
Другий закон Ньютона в релятивістській формі:
 . (1.114)
. (1.114)
Кінетична енергія тіла
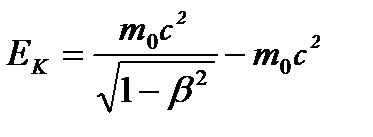 , (1.115)
, (1.115)
або якщо ввести релятивістську масу
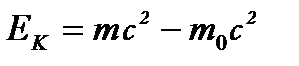 (1.116)
(1.116)
Повна релятивістська енергія
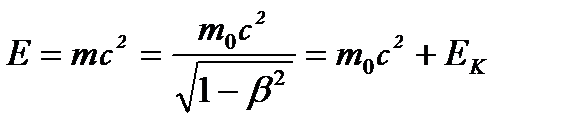 (1.117)
(1.117)
§ 9-11. МЕХАНІЧНІ КОЛИВАННЯ ТА ХВИЛІ
Рівняння вільних незатухаючих коливань і його розв'язок
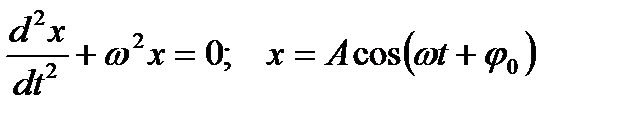 , (1.118)
, (1.118)
де 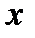 — зміщення;
— зміщення;  — амплітуда;
— амплітуда; 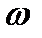 — власна частота коливань;
— власна частота коливань;  — початкова фаза.
— початкова фаза.
Швидкість і прискорення матеріальної точки, яка виконує гармонічне коливання,
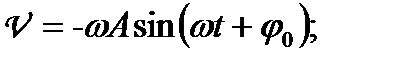 (1.119)
(1.119)
 . (1.120)
. (1.120)
Рівняння затухаючих коливань і його розв'язок
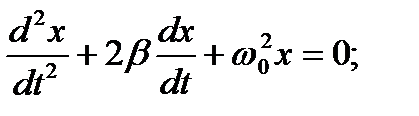 (1.121)
(1.121)
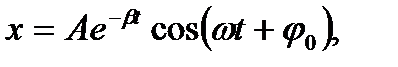 (1.122)
(1.122)
де 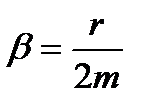 — коефіцієнт затухання;
— коефіцієнт затухання; 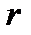 - коефіцієнт опору середовища;
- коефіцієнт опору середовища; 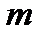 - маса тіла;
- маса тіла; 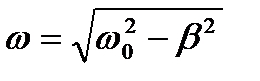 — циклічна частота коливань;
— циклічна частота коливань; 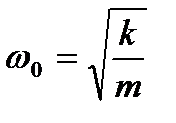 - частота незатухаючих коливань;
- частота незатухаючих коливань;  — амплітуда затухаючих коливань.
— амплітуда затухаючих коливань.
Логарифмічний декремент затухання
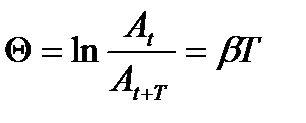 . (1.123)
. (1.123)
Добротність
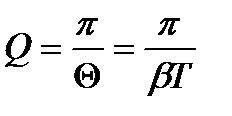 . (1.124)
. (1.124)
Рівняння вимушених коливань і його частинний розв'язок
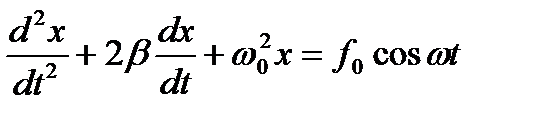 ; (1.125)
; (1.125)
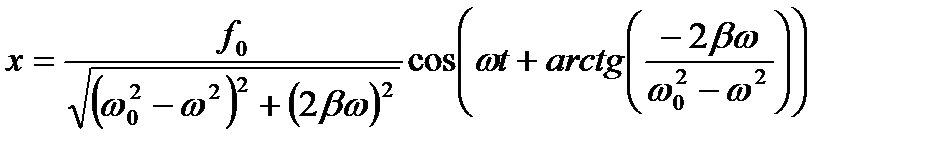 ,
,
де -  — амплітуда коливань;
— амплітуда коливань; 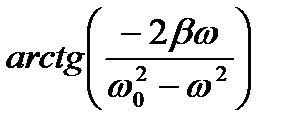 - початкова фаза;
- початкова фаза;  — зовнішня сила.
— зовнішня сила.
Резонансні значення циклічної частоти і амплітуди
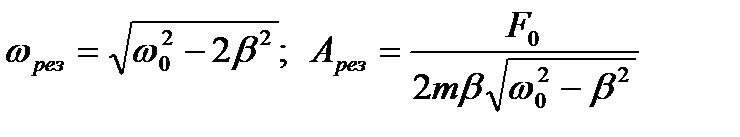 . (1.126)
. (1.126)
Додавання гармонічних коливань одного напрямку й однакової частоти. Амплітуда результуючого коливання
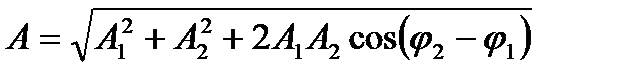 . (1.127)
. (1.127)
Початкова фаза результуючого коливання
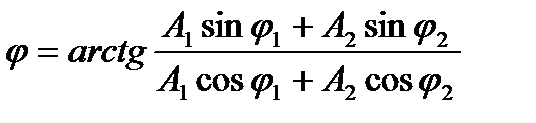 . (1.128)
. (1.128)
Траєкторія точки, яка бере участь у двох взаємно перпендикулярних коливаннях,
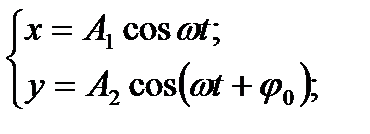 (1.129)
(1.129)
а)  , якщо різниця фаз
, якщо різниця фаз 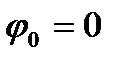 ;
;
б)  , якщо
, якщо 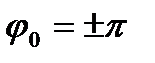 ;
;
в) 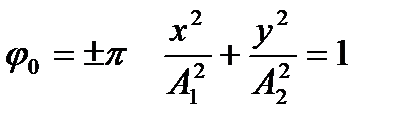 , якщо
, якщо 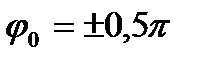 .
.
Період малих коливань математичного маятника
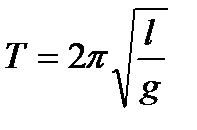 , (1.130)
, (1.130)
де 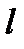 - довжина маятника;
- довжина маятника; 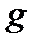 - прискорення вільного падіння.
- прискорення вільного падіння.
Період коливань тіла, підвішеного на пружині,
 , (1.131)
, (1.131)
де 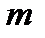 — маса тіла;
— маса тіла; 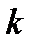 — жорсткість пружини.
— жорсткість пружини.
Період малих коливань фізичного маятника
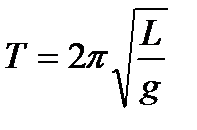 , (1.132)
, (1.132)
де 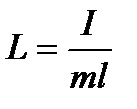 = зведена довжина фізичного маятника;
= зведена довжина фізичного маятника; 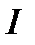 —момент інерції маятника відносно осі коливання;
—момент інерції маятника відносно осі коливання; 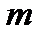 — маса маятника;
— маса маятника; 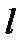 — відстань від центра мас до осі коливання.
— відстань від центра мас до осі коливання.
Повна енергія матеріальної точки масою 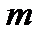 , яка здійснює гармонічні коливання
, яка здійснює гармонічні коливання
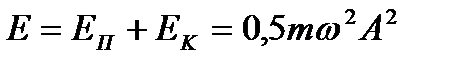 . (1.133)
. (1.133)
Рівняння плоскої монохроматичної біжучої хвилі
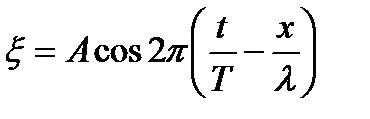 , (1.134)
, (1.134)
де 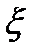 —зміщення довільної точки середовища на відстані
—зміщення довільної точки середовища на відстані 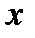 в момент часу
в момент часу 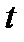 ;
; 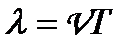 — довжина хвилі
— довжина хвилі 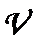 — швидкість поширення коливань у середовищі;
— швидкість поширення коливань у середовищі;  — період;
— період; 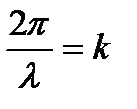 — хвильове число.
— хвильове число.
Швидкість поширення поздовжніх хвиль у пружному середовищі
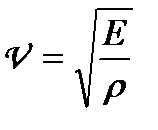 , (1.135)
, (1.135)
де 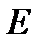 — модуль Юнга;
— модуль Юнга; 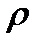 — густина середовища.
— густина середовища.
Швидкість поширення поперечних хвиль
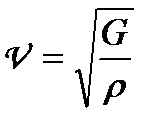 , (1.136)
, (1.136)
де 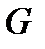 — модуль зсуву.
— модуль зсуву.
Кінетична енергія хвильового руху в об'ємі 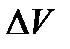
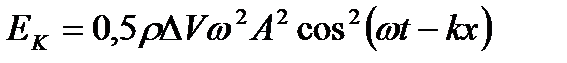 . (1.137)
. (1.137)
Потенціальна енергія хвильового руху
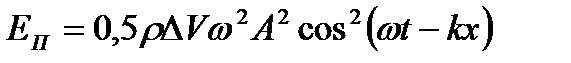 . (1.138)
. (1.138)
Повна енергія хвильового руху
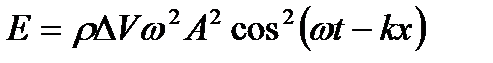 . (1.139)
. (1.139)
Середнє значення об'ємної густини енергії за часом
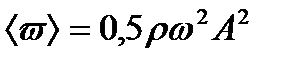 . (1.140)
. (1.140)
Потік енергії хвилі
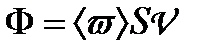 , (1.141)
, (1.141)
де 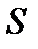 — поверхня, через яку переноситься енергія хвилі;
— поверхня, через яку переноситься енергія хвилі;  — швидкість хвилі.
— швидкість хвилі.
Середнє значення густини потоку енергії хвилі (вектор Умова)
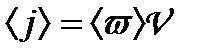 . (1.142)
. (1.142)
Рівень гучності звуку, дБ,
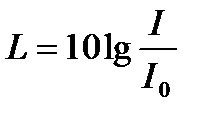 , (1.143)
, (1.143)
де 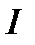 — інтенсивність звуку певної частоти;
— інтенсивність звуку певної частоти;  — інтенсивність на порозі чутності.
— інтенсивність на порозі чутності.
Ефект Доплера
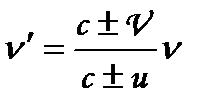 , (1.144)
, (1.144)
де 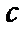 — швидкість поширення звуку;
— швидкість поширення звуку; 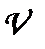 — швидкість руху приймача;
— швидкість руху приймача;  — швидкість руху джерела звуку;
— швидкість руху джерела звуку; 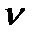 — частота від джерела. Верхні знаки беруться при зближенні джерела і приймача, нижні — при їх віддаленні.
— частота від джерела. Верхні знаки беруться при зближенні джерела і приймача, нижні — при їх віддаленні.
§ 12, 13. ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ РЕЧОВИНИ. СТАТИСТИЧНІ РОЗПОДІЛИ ТА ЯВИЩА ПЕРЕНОСУ В ГАЗАХ
Атомна одиниця маси 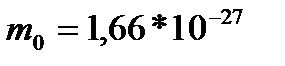 кг. Відносна молекулярна маса, або відносна маса молекули
кг. Відносна молекулярна маса, або відносна маса молекули
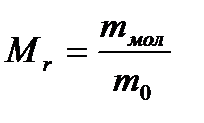 , (1.145)
, (1.145)
де 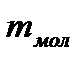 — абсолютне значення маси молекули, кг.
— абсолютне значення маси молекули, кг.
Відносна молекулярна маса речовини
 , (1.146)
, (1.146)
де  — кількість атомів
— кількість атомів 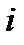 хімічного елемента, що входить до складу молекули даної речовини;
хімічного елемента, що входить до складу молекули даної речовини; 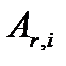 — відносна атомна маса цього елемента (відносні атомні маси наведено в таблиці Менделєєва).
— відносна атомна маса цього елемента (відносні атомні маси наведено в таблиці Менделєєва).
В одному молі довільної речовини міститься однакова кількість структурних елементів (стала Авогадро): 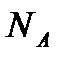 == 6,02. 1023 моль-1.
== 6,02. 1023 моль-1.
Молярна маса  (кг/моль). Кількість молів речовини
(кг/моль). Кількість молів речовини
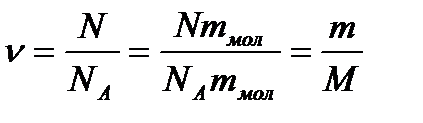 , (1.147)
, (1.147)
де 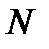 — кількість структурних елементів (молекул) речовини,
— кількість структурних елементів (молекул) речовини, 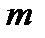 — маса речовини.
— маса речовини.
Кількість молів суміші речовин
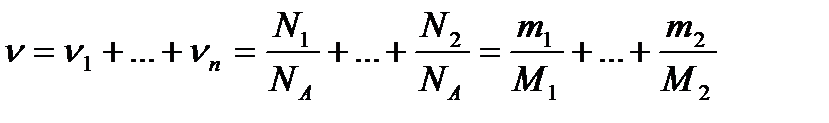 .
.
Основне рівняння кінетичної теорії газів
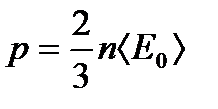 , (1.148)
, (1.148)
де 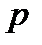 —тиск газу;
—тиск газу; 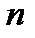 — концентрація молекул;
— концентрація молекул;  — середня кінетична енергія поступального руху молекули.
— середня кінетична енергія поступального руху молекули.
Середня енергія молекули
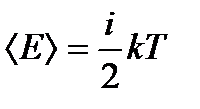 , (1.149)
, (1.149)
де 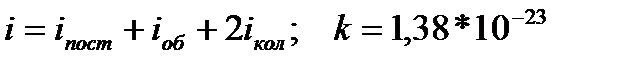 Дж/К — стала Больцмана;
Дж/К — стала Больцмана; 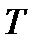 — термодинамічна температура газу.
— термодинамічна температура газу.
Залежність тиску газу від концентрації молекул і температури
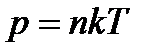 . (1.150)
. (1.150)
Рівняння стану ідеального газу (рівняння Менделєєва — Клапейрона)
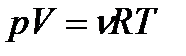 , (1.151)
, (1.151)
де  =8,31 Дж/(моль•К) — універсальна газова стала.
=8,31 Дж/(моль•К) — універсальна газова стала.
Тиск суміші газів (закон Дальтона)
 , (1.152)
, (1.152)
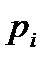 — парціальний тиск
— парціальний тиск 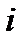 -ї компоненти суміші;
-ї компоненти суміші; 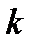 — число компонентів.
— число компонентів.
Молярна маса суміші газів
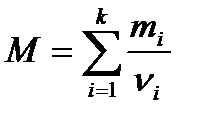 , (1.153)
, (1.153)
де 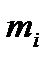 — маса
— маса 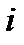 компоненти суміші;
компоненти суміші; 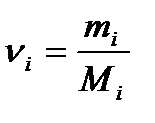 — кількість молів
— кількість молів 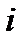 -ї компоненти
-ї компоненти
суміші.
Середня квадратична, середня арифметична і найбільш імовірна швидкості молекул
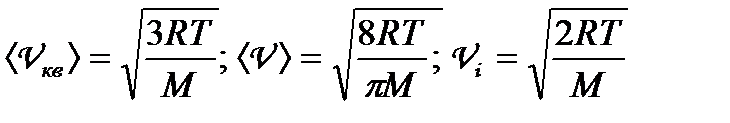 . (1.154)
. (1.154)
Розподіл Максвелла
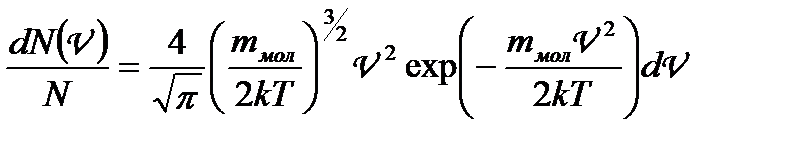 ,
,
або
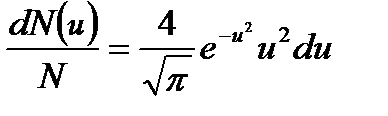 , (1.155)
, (1.155)
де 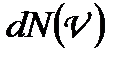 — кількість молекул, швидкості яких лежать в інтервалі від
— кількість молекул, швидкості яких лежать в інтервалі від 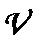 до
до 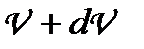 ;
;  — загальна кількість молекул;
— загальна кількість молекул; 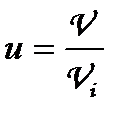 — відносна швидкість молекул.
— відносна швидкість молекул.
Барометрична формула
 , (1.156)
, (1.156)
де 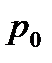 і
і 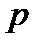 — тиск газу відповідно на висоті
— тиск газу відповідно на висоті 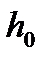 і
і 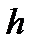 .
.
Розподіл Больцмана
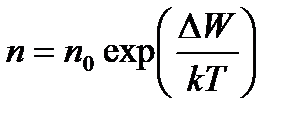 , (1.157)
, (1.157)
де 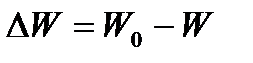 — різниця потенціальних енергій частинок (молекул) на двох рівнях довільного потенціального поля,
— різниця потенціальних енергій частинок (молекул) на двох рівнях довільного потенціального поля, 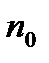 і
і 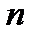 — концентрації частинок (молекул) на цих рівнях.
— концентрації частинок (молекул) на цих рівнях.
Розподіл Максвелла — Больцмана
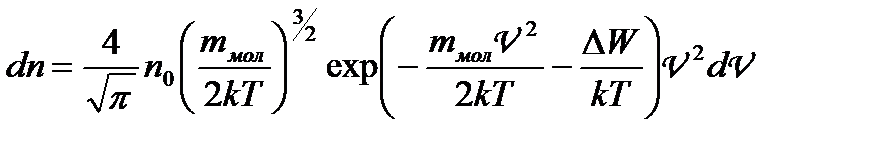 Середня довжина вільного пробігу молекул газу
Середня довжина вільного пробігу молекул газу
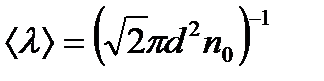 , (1.158)
, (1.158)
де 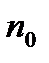 — концентрація молекул,
— концентрація молекул, 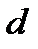 — ефективний діаметр молекули.
— ефективний діаметр молекули.
Середня кількість зіткнень однієї молекули за одиницю часу
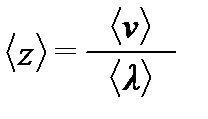 . (1.159)
. (1.159)
Кількість зіткнень усіх молекул в одиниці об'єму за одиницю часу
 . (1.160)
. (1.160)
Середнє число ударів молекул за одиницю часу об одиничну плоску поверхню, розміщену в газі,
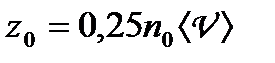 . (1.161)
. (1.161)
Маса газу 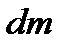 , перенесеного під час дифузії за час
, перенесеного під час дифузії за час 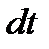 через плоску поверхню
через плоску поверхню 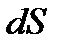 , розміщену перпендикулярно до осі
, розміщену перпендикулярно до осі 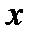 , при градієнті густини вздовж цієї осі
, при градієнті густини вздовж цієї осі 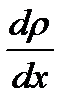 (закон Фіка),
(закон Фіка),
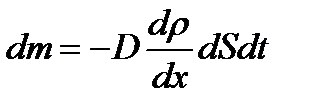 , (1.162)
, (1.162)
де 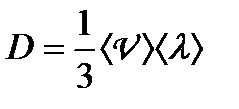 — коефіцієнт дифузії. (1.162. а)
— коефіцієнт дифузії. (1.162. а)
Сила внутрішнього тертя 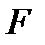 між двома шарами газу площею
між двома шарами газу площею 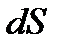 , що рухаються з різними швидкостями (закон Ньютона),
, що рухаються з різними швидкостями (закон Ньютона),
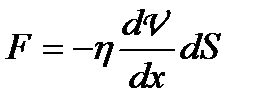 , (1.163)
, (1.163)
де 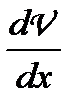 — градієнт швидкості течії газу в перпендикулярному до
— градієнт швидкості течії газу в перпендикулярному до 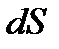 напрямі. Знак «мінус» означає, що сила тертя, яка діє на більш швидкі шари газу, напрямлена проти швидкості;
напрямі. Знак «мінус» означає, що сила тертя, яка діє на більш швидкі шари газу, напрямлена проти швидкості; 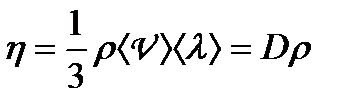 — коефіцієнт динамічної в’язкості. (1.163.а)
— коефіцієнт динамічної в’язкості. (1.163.а)
Кількість теплоти, яка переноситься внаслідок теплопровідності за час 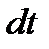 через плоску поверхню
через плоску поверхню 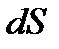 при градієнті температури
при градієнті температури 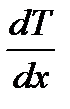 , перпендикулярному до
, перпендикулярному до 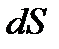 ,
,
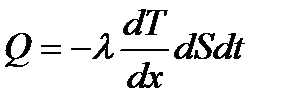 , (1.164)
, (1.164)
де 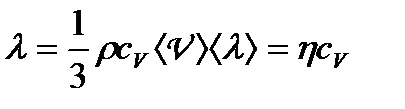 — коефіцієнт теплопровідності; (1. 164.а)
— коефіцієнт теплопровідності; (1. 164.а)
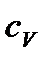 — питома теплоємність газу при сталому об'ємі.
— питома теплоємність газу при сталому об'ємі.
§ 14. ПЕРШЕ НАЧАЛО ТЕРМОДИНАМІКИ
Перше начало термодинаміки
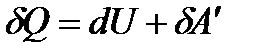 , (1.165)
, (1.165)
де 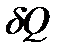 - елементарна кількість теплоти, що підводиться до термодинамічної системи;
- елементарна кількість теплоти, що підводиться до термодинамічної системи; 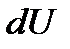 - зміна внутрішньої енергії системи;
- зміна внутрішньої енергії системи; 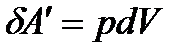 - робота, виконувана системою проти зовнішніх сил при нескінченно малій зміні об’єму.
- робота, виконувана системою проти зовнішніх сил при нескінченно малій зміні об’єму.
Зміна внутрішньої енергії ідеального газу
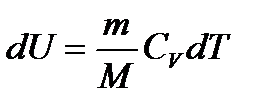 , (1.166)
, (1.166)
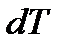 — зміна температури;
— зміна температури; 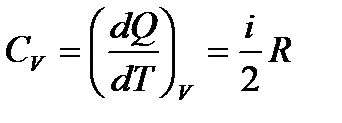 - молярна теплоємність газу при ізохорному процесі;
- молярна теплоємність газу при ізохорному процесі; 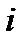 - кількість ступенів вільності молекул газу.
- кількість ступенів вільності молекул газу.
Молярна теплоємність газу при ізобарному процесі (рівняння Майєра)
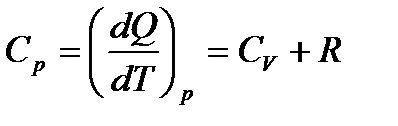 . (1.167)
. (1.167)
Робота, виконувана газом при ізобарному процесі,
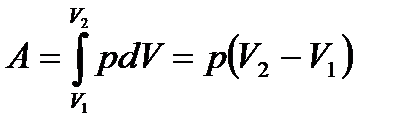 . (1.168)
. (1.168)
Робота при ізотермічному процесі
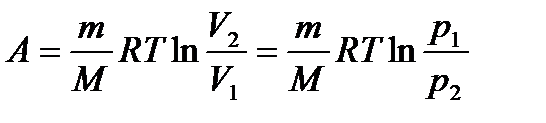 . (1.169)
. (1.169)
Рівняння адіабатного процесу (рівняння Пуассона)
 , (1.170)
, (1.170)
або 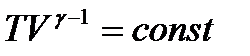 , (1.170,а)
, (1.170,а)
або 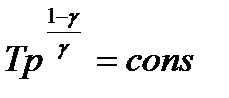 , (1.170,б)
, (1.170,б)
де 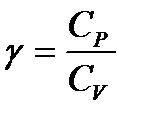 — показник адіабати.
— показник адіабати.
Робота при адіабатному процесі
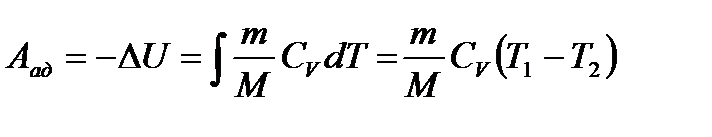 ,
,
або
 . (1.170, в)
. (1.170, в)
Рівняння політропного процесу
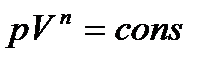 , (1.171)
, (1.171)
де  — показник політропи;
— показник політропи;  — молярна теплоємність газу при політропному процесі.
— молярна теплоємність газу при політропному процесі.
Робота при політропному процесі
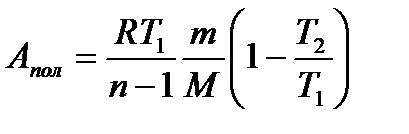 , (1.172)
, (1.172)
або
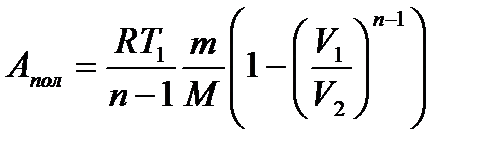 . (1.173)
. (1.173)
§ 15. ДРУГЕ НАЧАЛО ТЕРМОДИНАМІКИ
Коефіцієнт корисної дії (ККД) теплової машини
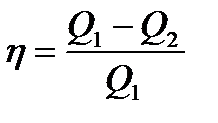 , (1.174)
, (1.174)
де 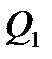 — кількість теплоти, яку дістає робоче тіло від нагрівника;
— кількість теплоти, яку дістає робоче тіло від нагрівника;  — кількість теплоти, яка передається робочим тілом холодильнику.
— кількість теплоти, яка передається робочим тілом холодильнику.
ККД ідеального циклу Карно
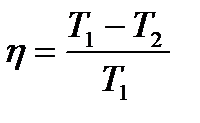 , (1.175)
, (1.175)
де 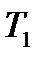 — температура нагрівача;
— температура нагрівача; 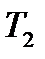 — температура холодильника.
— температура холодильника.
Холодильний коефіцієнт холодильної машини
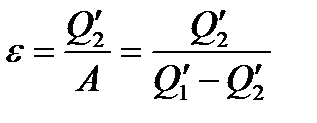 , (1.176)
, (1.176)
де 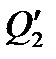 — кількість теплоти, яка відбирається від охолоджуваного тіла за цикл;
— кількість теплоти, яка відбирається від охолоджуваного тіла за цикл; 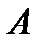 — робота, виконувана над робочим тілом за цикл;
— робота, виконувана над робочим тілом за цикл; 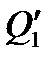 — кількість теплоти, яка передається навколишньому середовищу.
— кількість теплоти, яка передається навколишньому середовищу.
Холодильний коефіцієнт ідеального оберненого циклу Карно
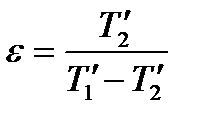 , (1.177)
, (1.177)
де 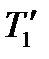 — температура середовища, якому передається теплота;
— температура середовища, якому передається теплота; 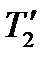 — температура охолоджуваного тіла.
— температура охолоджуваного тіла.
Приріст ентропії 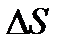 при переході термодинамічної системи із стану 1 у стан 2
при переході термодинамічної системи із стану 1 у стан 2
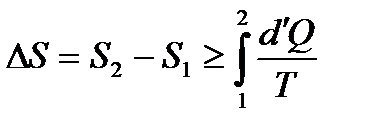 . (1.178)
. (1.178)
Адіабатний процес (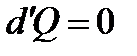 ). Для оборотного процесу маємо
). Для оборотного процесу маємо
 , звідси
, звідси  , (1.179)
, (1.179)
тобто оборотні адіабатні процеси є ізоентропійними.
Для оборотного ізотермічного процесу між двома станами 1 і 2 маємо
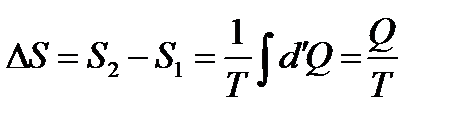 . (1.180)
. (1.180)
З рівняння (1.165), оскільки 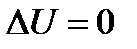 ,маємо
,маємо 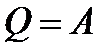 , а робота в ізотермічному процесі дорівнює (1.169), тому вираз (1.180) можно записати у вигляді:
, а робота в ізотермічному процесі дорівнює (1.169), тому вираз (1.180) можно записати у вигляді:
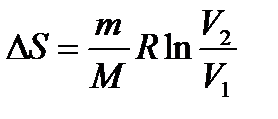 . (1.181)
. (1.181)
Ізохорний процес (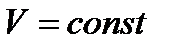 ). При сталому об’ємові
). При сталому об’ємові 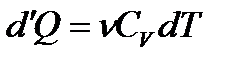 , тому
, тому
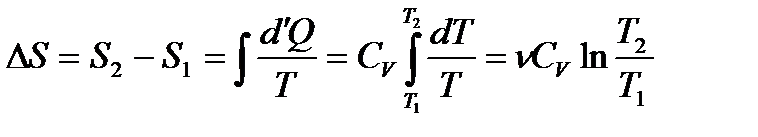 .(1.182)
.(1.182)
Ізобарний процес (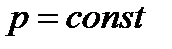 ). При цьому
). При цьому 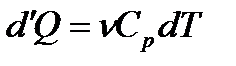 і приріст ентропії
і приріст ентропії
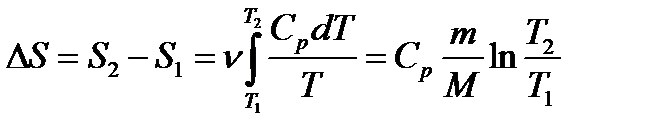 . (1.183)
. (1.183)
Ентропія 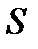 і термодинамічна ймовірність (статистична вага)
і термодинамічна ймовірність (статистична вага) 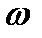 зв'язані співвідношенням
зв'язані співвідношенням 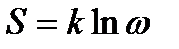 , де
, де 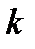 — стала Больцмана.
— стала Больцмана.
§ 16. РЕАЛЬНІ ГАЗИ 1 РІДИНИ
Рівняння Ван-дер-Ваальса для довільної маси пг газу
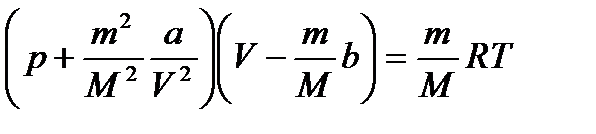 , (1.179)
, (1.179)
де 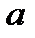 і
і  — сталі Ван-дер-Ваальса. В цьому рівнянні
— сталі Ван-дер-Ваальса. В цьому рівнянні 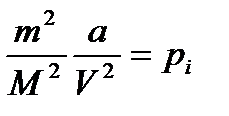 —тиск, зумовлений силами взаємодії молекул,
—тиск, зумовлений силами взаємодії молекул,  — об'єм, зв'язаний з власним об'ємом молекул.
— об'єм, зв'язаний з власним об'ємом молекул.
Зв'язок критичних параметрів — молярного об'єму, тиску і температури газу — із сталими  і
і 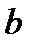 Ван-дер-Ваальса
Ван-дер-Ваальса
 . (1.180)
. (1.180)
Стала Ван-дер-Ваальса  , де
, де 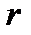 — радіус молекули газу,
— радіус молекули газу, 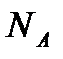 — стала Авогадро.
— стала Авогадро.
Зв'язок між критичними параметрами моля речовини
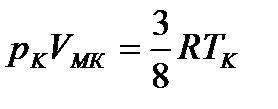 . (1.181)
. (1.181)
Рівняння Ван-дер-Ваальса у зведених величинах для одного моля газу
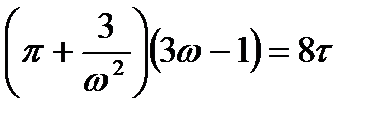 , (1.182)
, (1.182)
де 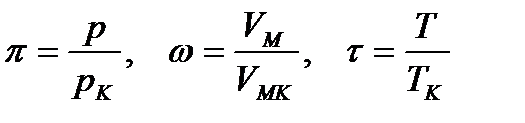 .
.
Зміна температури при дроселюванні реального газу в об'єм з невеликим тис
ком
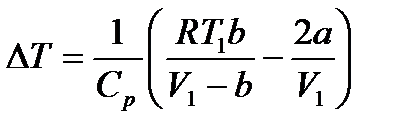 , (1.183)
, (1.183)
де 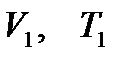 — початковий об'єм і початкова температура газу.
— початковий об'єм і початкова температура газу.
Відносна вологість повітря
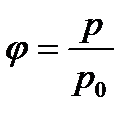 , або
, або 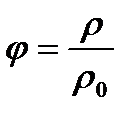 , (1.184)
, (1.184)
де 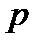 і
і  — відповідно парціальний тиск і густина водяної пари, що знаходиться в повітрі при даній температурі (абсолютна вологість);
— відповідно парціальний тиск і густина водяної пари, що знаходиться в повітрі при даній температурі (абсолютна вологість); 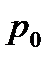 і
і 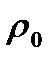 —парціальний тиск і густина насиченої водяної пари при тій самій температурі.
—парціальний тиск і густина насиченої водяної пари при тій самій температурі.
Рівняння Клапейрона - Клаузіуса
 , (1.185)
, (1.185)
де 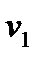 і
і 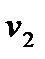 — питомі об'єми речовини в двох станах;
— питомі об'єми речовини в двох станах; 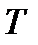 і
і 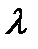 — температура і питома теплота переходу речовини із стану 1 в 2.
— температура і питома теплота переходу речовини із стану 1 в 2.
Коефіцієнт поверхневого натягу
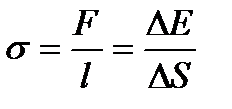 , (1.186)
, (1.186)
де 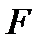 — сила поверхневого натягу;
— сила поверхневого натягу; 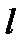 — довжина ділянки контуру, що обмежує вільну поверхню;
— довжина ділянки контуру, що обмежує вільну поверхню; 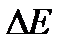 — зміна вільної енергії поверхневого шару рідини;
— зміна вільної енергії поверхневого шару рідини; 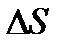 — зміна площі цього шару.
— зміна площі цього шару.
Надлишковий тиск, зумовлений кривизною поверхні рідини (формула Лапласа),
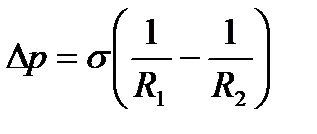 , (1.187)
, (1.187)
де 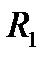 і
і  — радіуси кривизни двох взаємно перпендикулярних перерізів поверхні рідини.
— радіуси кривизни двох взаємно перпендикулярних перерізів поверхні рідини.
Висота підняття рідини в капілярних трубках
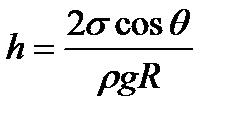 , (1.188)
, (1.188)
де 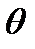 — крайовий кут змочування;
— крайовий кут змочування;  — густина рідини;
— густина рідини;  — радіус капілярної трубки.
— радіус капілярної трубки.
Відносна зміна об'єму рідини при нагріванні
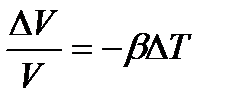 , (1.189)
, (1.189)
де 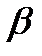 — температурний коефіцієнт об'ємного розширення.
— температурний коефіцієнт об'ємного розширення.
Відносна зміна об'єму рідини при зміні тиску
 , (1.190)
, (1.190)
де  — коефіцієнт стисливості.
— коефіцієнт стисливості.
Осмотичний тиск розчину (1.формула Вант-Гоффа)
 , (1.191)
, (1.191)
де 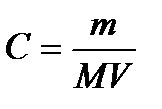 — кількість молів розчиненої речовини в одиниці об'єму розчинника.
— кількість молів розчиненої речовини в одиниці об'єму розчинника.
§ 17. ТЕПЛОВІ ВЛАСТИВОСТІ ТВЕРДИХ ТІЛ. ФАЗОВІ ПЕРЕХОДИ
Стала кристалічної решітки кубічної системи
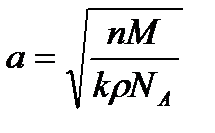 , (1.192)
, (1.192)
де 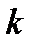 — кількість однакових атомів у хімічній формулі кристалічного тіла;
— кількість однакових атомів у хімічній формулі кристалічного тіла; 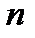 — кількість однакових атомів, які утворюють елементарну комірку;
— кількість однакових атомів, які утворюють елементарну комірку; 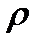 — густина кристала;
— густина кристала; 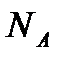 — число Авогадро;
— число Авогадро; 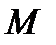 — молярна маса речовини.
— молярна маса речовини.
Відносна зміна довжини при зміні температури на ДТ
 , (1.193)
, (1.193)
де 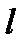 — початкова довжина;
— початкова довжина;  — зміна довжини;
— зміна довжини; 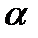 — коефіцієнт лінійного теплового розширення.
— коефіцієнт лінійного теплового розширення.
Для твердих ізотропних тіл 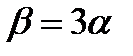 , де
, де 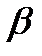 — коефіцієнт об'ємного теплового розширення.
— коефіцієнт об'ємного теплового розширення.
Молярна теплоємність хімічно простих твердих тіл в класичній теорії теплоємності (закон Дюлонга — Пті)
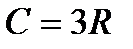 . (1.194)
. (1.194)
Кількість теплоти, яка передається твердими тілами внаслідок теплопровідності,
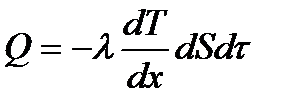 , (1.195)
, (1.195)
де 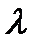 — коефіцієнт теплопровідності;
— коефіцієнт теплопровідності; 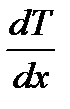 - градієнт температури в напрямі, перпендикулярному до поверхні, площа якої
- градієнт температури в напрямі, перпендикулярному до поверхні, площа якої  ;
; 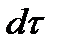 — час процесу теплопередачі.
— час процесу теплопередачі.
Теплопередача від одного середовища до іншого через площу 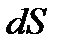 за час
за час 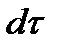
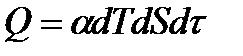 , (1.196)
, (1.196)
де 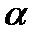 — коефіцієнт тепловіддачі.
— коефіцієнт тепловіддачі.
Рівняння Клапейрона — Клаузіуса для зміни температури плавлення 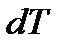 при зміні тиску
при зміні тиску  буде
буде
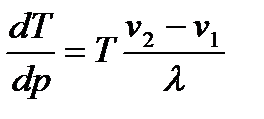 , (1.197)
, (1.197)
де 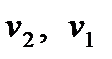 — питомі об'єми речовини відповідно в твердому і рідкому станах;
— питомі об'єми речовини відповідно в твердому і рідкому станах; 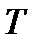 — температура плавлення;
— температура плавлення; 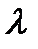 — питома теплота плавлення.
— питома теплота плавлення.
Розділ III ЕЛЕКТРИКА І МАГНЕТИЗМ
§ 18. ЕЛЕКТРИЧНЕ ПОЛЕ
За законом Кулона сила, з якою взаємодіють два точкових заряди q1 і q2, визначається за формулою
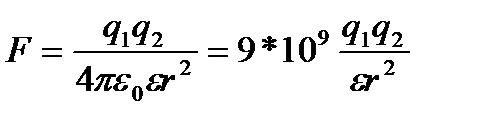 , (2.1)
, (2.1)
де r — відстань між зарядами; 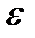 — відносна діелектрична проникність середовища
— відносна діелектрична проникність середовища 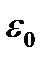 = 8,854*10-12 Ф/м - електрична стала.
= 8,854*10-12 Ф/м - електрична стала.
Об'ємна густина заряду
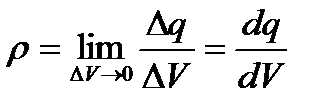 , Кл/м3. (2.2)
, Кл/м3. (2.2)
Поверхнева густина заряду
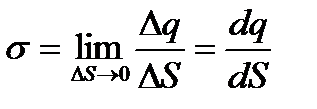 , Кл/м2. (2.3)
, Кл/м2. (2.3)
Лінійна густина заряду
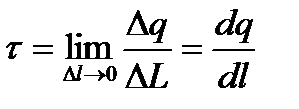 . (2.4)
. (2.4)
Напруженість 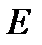 і потенціал
і потенціал  у даній точці поля
у даній точці поля
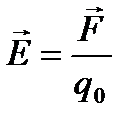 ,
, 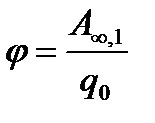 (2.5)
(2.5)
де F - сила, з якою поле діє на пробний заряд  ,
,  - робота по переміщенню пробного заряду із нескінченності у дану точку полю.
- робота по переміщенню пробного заряду із нескінченності у дану точку полю.
Напруженість і потенціал поля, створеного точковим зарядом q на відстані r від заряду,
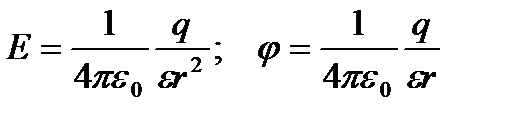 . (2.6)
. (2.6)
Напруженість результуючого поля системи n зарядів дорівнює векторній сумі напруженостей полів, створених кожним з цих зарядів окремо,
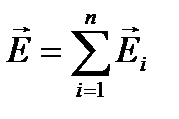 , (2.7)
, (2.7)
За теоремою Остроградського - Гаусса потік напруженості та потік електричної індукції 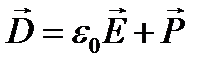 (де
(де 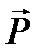 - вектор поляризації) через довільну замкнену поверхню
- вектор поляризації) через довільну замкнену поверхню
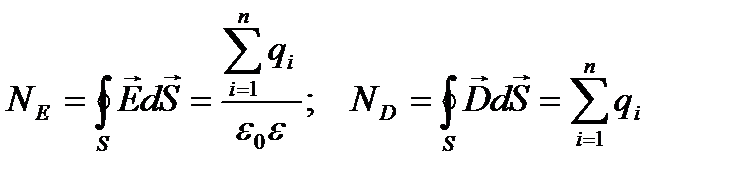 , (2.8)
, (2.8)
дe 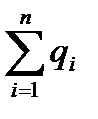 - алгебраїчна сума зарядів, які знаходяться всередині замкненої поверхні, при цьому циркуляція вектора напруженості по замкненому колу дорівнює
- алгебраїчна сума зарядів, які знаходяться всередині замкненої поверхні, при цьому циркуляція вектора напруженості по замкненому колу дорівнює
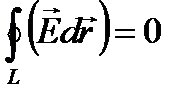 . (2.8,а)
. (2.8,а)
Модуль напруженості поля, створеного рівномірно зарядженою нескінченною площиною,
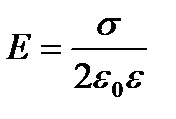 . (2.9)
. (2.9)
Модуль напруженість поля, створеного різнойменне зарядженими паралельними нескінченними площинами (поле плоского конденсатора),
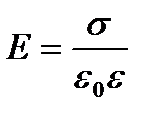 . (2.10)
. (2.10)
Модуль напруженості поля, створеного зарядженою нескінченно довгою ниткою,
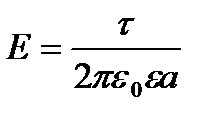 , (2.11)
, (2.11)
де а - відстань від нитки до точки, в якій визначається напруженість.
Напруженість поля, створеного нескінченно довгим рівномірно зарядженим циліндром,
 , (2.12)
, (2.12)
де r відстань від осі циліндра до точки, в якій визначається напруженість.
Модуль напруженості електростатичного поля сфери радіуса R, заряд q якої рівномірно розподілений по її поверхні, на відстані r від центра:
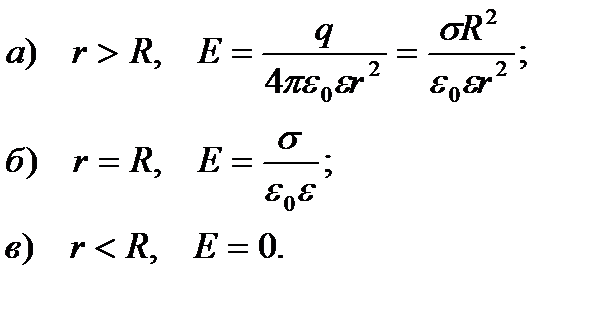 (2.13)
(2.13)
Модуль напруженості поля кулі радіуса R., рівномірно зарядженої по об'єму, на відстані r від центра:
 (2.14)
(2.14)
Зв’язок між напруженістю та потенціалом поля:
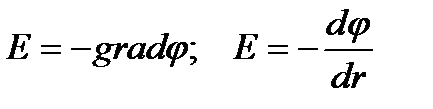 . (2.15)
. (2.15)
Для однорідного поля (поля плоского конденсатора) напруженість
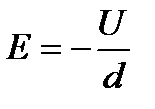 , (2.16)
, (2.16)
де U — різниця потенціалів між пластинами конденсатора; d — відстань між ними.
§ 19. ЕЛЕКТРИЧНЕ ПОЛЕ В РЕЧОВИНІ
Для кожного відокремленого провідника відношення заряду до потенціалу провідника є величина стала
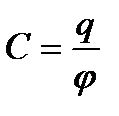 , (2.17)
, (2.17)
де  — електрична ємність провідника.
— електрична ємність провідника.
Ємність плоского і циліндричного конденсаторів:
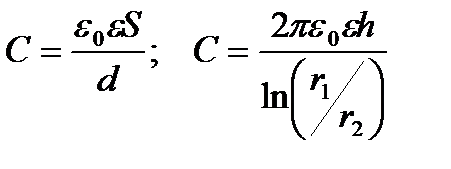 , (2.18)
, (2.18)
де 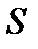 — площа кожної пластини;
— площа кожної пластини; 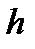 — висота коаксіальних циліндрів;
— висота коаксіальних циліндрів; 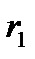 і
і  — радіуси внутрішнього та зовнішнього циліндрів відповідно.
— радіуси внутрішнього та зовнішнього циліндрів відповідно.
Ємність сферичного конденсатора
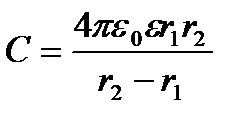 , (2.19)
, (2.19)
де 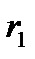 і
і  — радіус внутрішньої і зовнішньої сфер.
— радіус внутрішньої і зовнішньої сфер.
Ємність провідної кулі радіуса г
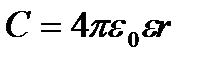 . (2.20)
. (2.20)
При паралельному з'єднанні конденсаторів ємність батареї дорывнюэ
 , (2.21)
, (2.21)
при послідовному з'єднанні
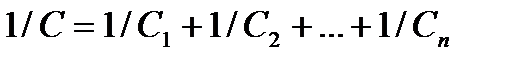 . (2.22)
. (2.22)
Електрична енергія відокремленого зарядженого провідника
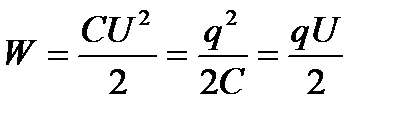 . (2.23)
. (2.23)
Для плоского конденсатора
 , (2.24)
, (2.24)
де 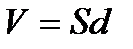 — об'єм, обмежений пластинами конденсатора.
— об'єм, обмежений пластинами конденсатора.
Об'ємна густина енергії електричного поля
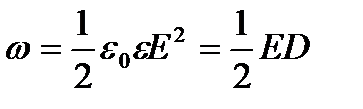 , (2.25)
, (2.25)
де 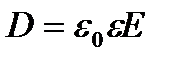 - електричне зміщення, Кл/м2.
- електричне зміщення, Кл/м2.
Сила притягання пластин плоского конденсатора
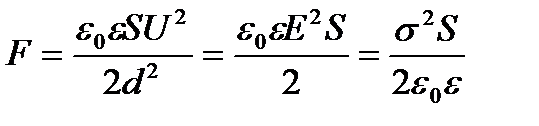 . (2.26)
. (2.26)
§ 20. ПОСТІЙНИЙ ЕЛЕКТРИЧНИЙ СТРУМ
Сила електричного струму чисельно дорівнює зміні заряду, перенесеного через поперечний переріз провідника, залежно від часу
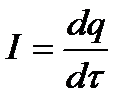 . (2.27)
. (2.27)
Силу постійного струму визначають із співвідношення
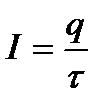 . (2.28)
. (2.28)
Густину струму вимірюють відношенням сили струму до площі поперечного перерізу провідника
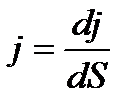 . (2.29)
. (2.29)
Закон Ома для ділянки електричного кола
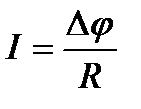 , (2.30)
, (2.30)
де 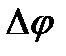 — різниця потенціалів на кінцях ділянки;
— різниця потенціалів на кінцях ділянки; 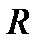 — опір цієї ділянки.
— опір цієї ділянки.
Опір циліндричного провідника довжиною  та площею поперечного перерізу
та площею поперечного перерізу 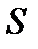
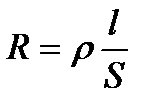 , (2.31)
, (2.31)
де 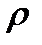 — питомий опір.
— питомий опір.
Питомий опір провідника залежить від його температури
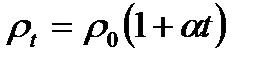 , (2.32)
, (2.32)
де 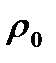 — питомий опір при 0 °С;
— питомий опір при 0 °С; 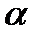 — температурний коефіцієнт опору.
— температурний коефіцієнт опору.
Закон Ома для неоднорідної ділянки кола
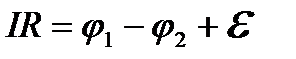 . (2.33)
. (2.33)
де 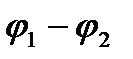 — напруга на даній ділянці кола;
— напруга на даній ділянці кола; 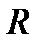 — сума всіх опорів ділянки;
— сума всіх опорів ділянки;  — ЕРС джерела струму.
— ЕРС джерела струму.
Закон Ома в диференціальній формі
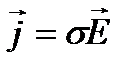 , (2.34)
, (2.34)
де 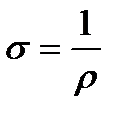 — питома електропровідність матеріалу.
— питома електропровідність матеріалу.
Закон Ома для повного кола
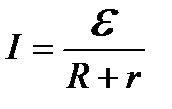 , (2.35)
, (2.35)
де  — зовнішній опір;
— зовнішній опір; 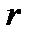 — внутрішній опір.
— внутрішній опір.
Робота струму на ділянці кола
 . (2.36)
. (2.36)
Потужність чисельно дорівнює роботі постійного струму за одиницю часу
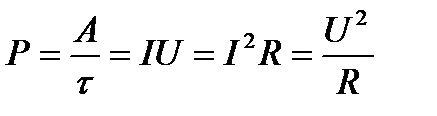 . (2.38)
. (2.38)
Потужність повного електричного кола
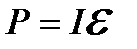 . (2.39)
. (2.39)
Відношення корисної потужності до загальної потужності визначає ККД джерела струму
 . (2.40)
. (2.40)
Кількість теплоти 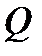 , що виділяється в провіднику при проходженні в ньому постійного струму (закон Джоуля — Ленца),
, що виділяється в провіднику при проходженні в ньому постійного струму (закон Джоуля — Ленца),
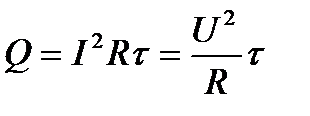 . (2.41)
. (2.41)
Закон Джоуля — Ленца в диференціальній формі
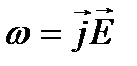 , (2.42)
, (2.42)
де 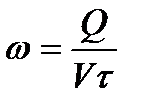 — питома густина теплової потужності.
— питома густина теплової потужності.
 2017-10-25
2017-10-25 1392
1392
