1. Алгебраїчна сума всіх сил струмів, що сходяться у вузлі розгалуженого кола, дорівнює нулю:
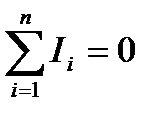 . (2.43)
. (2.43)
Струми, що входять у вузол, вважають додатними, які виходять — від'ємними,
або навпаки.
2. У будь-якому простому замкненому контурі, довільно обраному у розгалуженому електричному колі, алгебраїчна сума добутків сил струмів на опори відповідних ділянок цього контуру дорівнює алгебраїчній сумі електрорушійних сил, що діють у ньому
 . (2.44)
. (2.44)
При користуванні правилами Кірхгофа струмам приписують певні напрями. Струми вважаються додатними, якщо їхній напрям збігається з напрямом обходу по замкненому контуру, а від'ємними будуть струми, напрям яких протилежний напряму обходу по контуру. Електрорушійні сили вважають додатними, якщо їхній власний струм збігається з напрямом обходу, тобто ті ЕРС, для яких напрям обходу збігається з переходом від негативного до позитивного полюса. У противному разі ЕРС вважають від'ємними.
§ 21. ЕЛЕКТРИЧНИЙ СТРУМ У МЕТАЛАХ, ВАКУУМІ ТА ГАЗАХ
Для металів густина струму
 , (2.45)
, (2.45)
де  - концентрація електронів провідності;
- концентрація електронів провідності;  - заряд електрона;
- заряд електрона;  - середня швидкість напрямленого руху електронів.
- середня швидкість напрямленого руху електронів.
Питома електропровідність власних напівпровідників
 , (2.46)
, (2.46)
де  і
і  - рухливість електронів і дірок.
- рухливість електронів і дірок.
Рухливість носіїв заряду вимірюється середньою швидкістю яку він отримає в електричному колі з напруженістю 1 В/м.
Залежність питомої електропровідності власних напівпровідників від температури:
 , (2.47)
, (2.47)
де  - ширина забороненої зони;
- ширина забороненої зони;  - стала Больцмана:
- стала Больцмана:  - абсолютна температура;
- абсолютна температура; 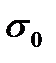 - стала величина, що визначається природою напівпровідника.
- стала величина, що визначається природою напівпровідника.
КОНТАКТНІ ЯВИЩА В МЕТАЛАХ І НАПІВПРОВІДНИКАХ
Робота виходу електрона з металу  .
.
Зовнішня контактна різниця потенціалів
 . (2.48)
. (2.48)
Внутрішня контактна різниця потенціалів
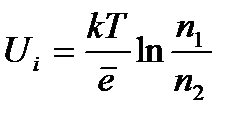 , (2.49)
, (2.49)
де  - концентрація електронів провідності в контактуючих металах.
- концентрація електронів провідності в контактуючих металах.
У певному інтервалі температур для деяких пар металів (наприклад, Сu—Ві, Аg—Сu, Рt—Fе, мідь — константан та ін.) термоЕРС залежить від різниці температур спаїв:
 , (2.50)
, (2.50)
де 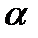 — коефіцієнт термоЕРС, який залежить від природи контактуючих металів.
— коефіцієнт термоЕРС, який залежить від природи контактуючих металів.
ЕЛЕКТРИЧНІ ЯВИЩА У ВАКУУМІ
Залежність термоелектронного струму від анодної напруги (коли немає насичення) виражається формулою Богуславського — Ленгмюра
 , (2.51)
, (2.51)
де В залежить від форми та розмірів електродів діода.
Для плоского електрода
 , (2.52)
, (2.52)
де d — відстань між плоскими електродами; S — площа поверхні катода (анода).
Залежність густини струму насичення від температури виражається формулою Річардсона — Дешмана
 , (2.53)
, (2.53)
де D — стала, що залежить від властивостей поверхні металу і для чистих металів дорівнює 6,02•105 А/(К2•м2); k — стала Больцмана; Т — термодинамічна температура катода.
Закон Ома для електролітів має вигляд
 , (2.54)
, (2.54)
де 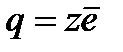 - заряд іона (z - валентність);
- заряд іона (z - валентність); 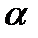 - коефіцієнт дисоціації;
- коефіцієнт дисоціації;  - концентрація розчиненої речовини;
- концентрація розчиненої речовини;  - рухливості позитивних і негативних іонів,
- рухливості позитивних і негативних іонів,  - питома електропровідність електроліту, або
- питома електропровідність електроліту, або 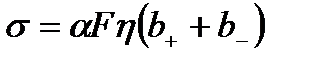 , де
, де  - еквівалентна концентрація розчину.
- еквівалентна концентрація розчину.
Еквівалентна електропровідність
 . (2.55)
. (2.55)
Перший закон Фарадея
 , (2.56)
, (2.56)
де k - електрохімічний еквівалент.
Другий закон Фарадея
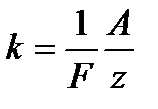 , (2.57)
, (2.57)
де А - атомна маса;  Кл/моль - число Фарадея; z - валентність речовин.
Кл/моль - число Фарадея; z - валентність речовин.
ЕЛЕКТРИЧНИЙ СТРУМ У ГАЗАХ
При малих густинах струму, який проходить у газі, має місце закон Ома:
 , (2.58)
, (2.58)
де  - рухливості іонів газу; n - концентрація позитивних і негативних іонів;
- рухливості іонів газу; n - концентрація позитивних і негативних іонів;  (кількість пар іонів). Насичення немає. При цьому
(кількість пар іонів). Насичення немає. При цьому
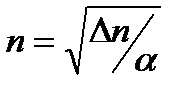 , (2.59)
, (2.59)
де  - кількість пар іонів, які утворюються під дією іонізатора щосекунди в одиниці об'єму;
- кількість пар іонів, які утворюються під дією іонізатора щосекунди в одиниці об'єму; 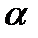 - коефіцієнт рекомбінації.
- коефіцієнт рекомбінації.
Густина струму насичення між плоскими електродами, які знаходяться на відстані d один від одного,
 . (2.60)
. (2.60)
§ 22. ПОСТІЙНЕ МАГНІТНЕ ПОЛЕ
Вектор індукції магнітного поля
 . (2.61)
. (2.61)
Індукція магнітного поля пов'язана з напруженістю таким співвідношенням:
 , (2.62)
, (2.62)
де  , - відносна магнітна проникність середовища;
, - відносна магнітна проникність середовища; 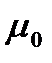 =
=  *10-7 Гн/м — магнітна стала. Для вакууму
*10-7 Гн/м — магнітна стала. Для вакууму  = 1.
= 1.
Магнітна індукція в центрі колового провідника із струмом радіуса R
 . (2.63)
. (2.63)
Індукція в будь-якій точці на осі колового провідника із струмом
 . (2.64)
. (2.64)
Індукція на відстані 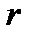 від лінійного провідника із струмом
від лінійного провідника із струмом
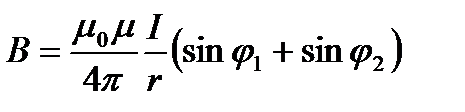 , (2.65)
, (2.65)
де  - кути під якими видно кінці провідника.
- кути під якими видно кінці провідника.
Для нескінченно довгого провідника  і, отже,
і, отже,
 . (2.66)
. (2.66)
Для симетричного розміщення кінців провідника відносно розглядуваної точки
 . (2.67)
. (2.67)
Індукція в центрі дуги кола довжиною  радіуса
радіуса 
 . (2.68)
. (2.68)
Магнітна індукція у довільній точці на осі соленоїда
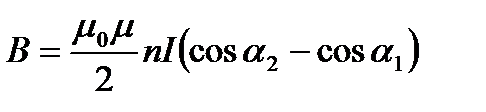 , (2.69)
, (2.69)
де  <
< 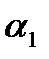 ;
;  — кількість витків на одиницю довжини.
— кількість витків на одиницю довжини.
Максимальне значення індукції в середині осі соленоїда
 , (2.70)
, (2.70)
де  — радіус витка соленоїда;
— радіус витка соленоїда;  — довжина соленоїда.
— довжина соленоїда.
Для нескінченно довгого соленоїда 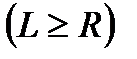 в середній його частині на осі
в середній його частині на осі
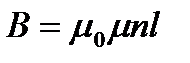 . (2.71)
. (2.71)
Принцип суперпозиції магнітних полів
 . (2.72)
. (2.72)
Для окремого випадку накладання двох полів абсолютне значення магнітної індукції
 , (2.73)
, (2.73)
де  — кут між векторами
— кут між векторами  , і
, і  .
.
Сила, що діє на провідник із струмом у магнітному полі (закон Ампера),
 . (2.74)
. (2.74)
Сила взаємодії двох нескінченно довгих провідників із струмом
 , (2.75)
, (2.75)
де  — відстань між провідниками;
— відстань між провідниками;  — довжина провідника.
— довжина провідника.
Магнітний момент рамки із струмом
 , (2.76)
, (2.76)
де 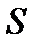 — площа рамки.
— площа рамки.
Магнітний момент соленоїда із струмом
 . (2.77)
. (2.77)
Період коливань магнітної стрілки або рамки із струмом у магнітному полі
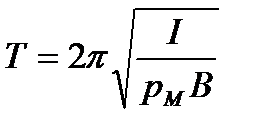 . (2.78)
. (2.78)
Модуль механічного моменту, що діє на рамку із струмом,
 . (2.79)
. (2.79)
Сила, що діє на рамку із струмом (магнітний диполь),
 , (2.80)
, (2.80)
де  - похідна вектора
- похідна вектора  по напрямку диполя.
по напрямку диполя.
Сила, що діє на рухомий заряд у магнітному полі (сила Лоренца),
 . (2.81)
. (2.81)
Закон повного струму
 . (2.82)
. (2.82)
або
 . (2.83)
. (2.83)
Магнітний потік через плоский контур
 , (2.84)
, (2.84)
де  — нормаль до площини контуру.
— нормаль до площини контуру.
Для неоднорідного поля
 . (2.85)
. (2.85)
Магнітний потік, який зчеплений з усіма витками соленоїда,
 , (2.86)
, (2.86)
де Ф — магнітний потік через один виток.
Робота переміщення провідника або замкнутого контуру із струмом у магнітному полі
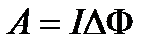 , (2.87)
, (2.87)
де  - потік, що перетинає провідник під час руху, або зміна потоку через площину контуру.
- потік, що перетинає провідник під час руху, або зміна потоку через площину контуру.
§ 23. ЕЛЕКТРОМАГНІТНА ІНДУКЦІЯ
Закон електромагнітної індукції (закон Фарадея — Максвелла)
 , (2.88)
, (2.88)
де  - число витків контуру.
- число витків контуру.
Заряд, що проходить через поперечний переріз провідника при електромагнітній індукції (закон Фарадея),
 . (2.89)
. (2.89)
Різниця потенціалів, яка виникає на кінцях провідника при його русі в магнітному полі,
 . (2.90)
. (2.90)
ЕРС індукції, яка виникає в рамці із струмом при її обертанні,
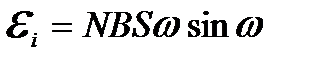 . (2.91)
. (2.91)
 Рис. 1. Рис. 1. |
 , (2.92)
, (2.92)
де 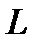 — індуктивність контуру.
— індуктивність контуру.
Індуктивність соленоїда
 . (2.93)
. (2.93)
Миттєве значення сили струму самоіндукції в контурі, який містить індуктивність, при замиканні кола
 . (2.94)
. (2.94)
А при розмиканні кола
 , (2.95)
, (2.95)
де  — час, який проходить після замикання (розмикання) кола;
— час, який проходить після замикання (розмикання) кола;  — сила струму в колі при (
— сила струму в колі при ( = 0).
= 0).
Магнітний потік, який створюється струмом у котушці з індуктивністю,
 . (2.96)
. (2.96)
Взаємна індуктивність двох контурів
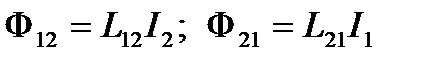 , (2.97)
, (2.97)
де  — коефіцієнт взаємоіндукції.
— коефіцієнт взаємоіндукції.
Енергія магнітного поля
 . (2.98)
. (2.98)
Об'ємна густина енергії магнітного поля соленоїда
 . (2.99)
. (2.99)
§ 25. МАГНІТНЕ ПОЛЕ В РЕЧОВИНІ
Закони магнітного кола для тороїда, який має повітряний проміжок,
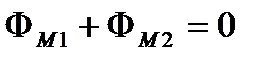 . (2.100)
. (2.100)
Із закону повного струму маємо
 , (2.101)
, (2.101)
або
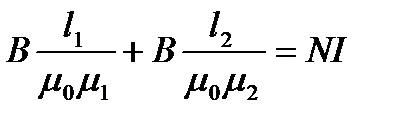 . (2.102)
. (2.102)
Звідси
 , (2.103)
, (2.103)
або
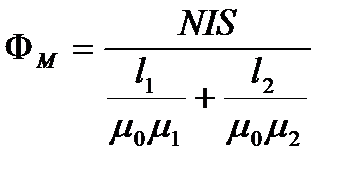 . (2.104)
. (2.104)
Зв'язок між напруженістю, індукцією і намагніченістю магнітного поля:
 . (2.105)
. (2.105)
Залежність індукції магнітного поля в речовині від напруженості зовнішнього поля для заліза і чавуну показано на рис. 1.
§ 24-26. ЗМІННИЙ СТРУМ. КОЛИВАННЯ 1 ХВИЛІ
Єфективні значення сили змінного струму та змінної напруги
 (2.106)
(2.106)
де  - період струму;
- період струму;  ,
,  - миттєві значення сили струму та напруги.
- миттєві значення сили струму та напруги.
У випадку синусоїдального струму
 ,
, 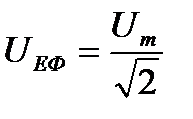 , (2.107)
, (2.107)
де  ,
,  - амплітуди сили струму та напруги.
- амплітуди сили струму та напруги.
При послідовному з’єднанні елементів кола повний опір змінному струму
 , (2.108)
, (2.108)
де  ,
,  і
і  - активний опір, індуктивність і ємність кола;
- активний опір, індуктивність і ємність кола;  - колова частота струму.
- колова частота струму.
Потужність змінного струму
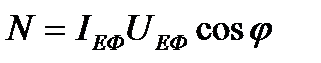 , (2.109)
, (2.109)
де  - зсув фаз між струмом і напругою.
- зсув фаз між струмом і напругою.
Період вільних затухаючих коливань коливального контуру
 . (2.110)
. (2.110)
Логарифмічний декремент затухання:
 . (2.111)
. (2.111)
Швидкість поширення електромагнітних коливань у ізотропному середовищі з діелектричній  і магнітній
і магнітній  проникністю
проникністю
 , (2.112)
, (2.112)
де  - швидкість електромагнітних хвиль у вакуумі.
- швидкість електромагнітних хвиль у вакуумі.
1. Вільні коливання в контурах
Частота вільних коливань в ідеальному контурі ( )
)
 . (2.113)
. (2.113)
Циклічна частота  .
.
Частота вільних коливань у реальному контурі ( )
)
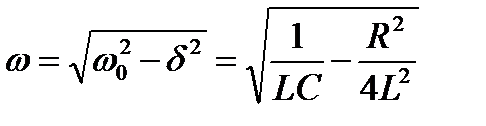 . (2.114)
. (2.114)
Хвильовий (характеристичний) опір контура
 . (2.115)
. (2.115)
Миттєві значення сили струму та напруги при затухаючих коливаннях
 ; (2.116)
; (2.116)
 ,(2.117)
,(2.117)
де  і
і  — початкові амплітуди сили струму і напруги при
— початкові амплітуди сили струму і напруги при  = 0;
= 0;  - коефіцієнт затухання коливань
- коефіцієнт затухання коливань
 . (2.118)
. (2.118)
 - зсув фаз між напругою і струмом,
- зсув фаз між напругою і струмом,
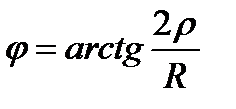 . (2.119)
. (2.119)
Стала часу коливального контуру  - час, через який амплітуда коливань зменшується в
- час, через який амплітуда коливань зменшується в  = 2,7 рази.
= 2,7 рази.
Під час вільних коливань у контурі відбувається періодична перетворення енергії  електричного поля конденсатора в енергію магнітного поля котушки індуктивності
електричного поля конденсатора в енергію магнітного поля котушки індуктивності  , і навпаки. Величини
, і навпаки. Величини  і
і 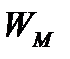 періодично змінюються від 0 до максимальних значень, які відповідно дорівнюють
періодично змінюються від 0 до максимальних значень, які відповідно дорівнюють
 і
і  , (2.120)
, (2.120)
причому дорівнюють одна одній.
Коливання  і
і 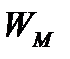 зсунуті за фазою на
зсунуті за фазою на  .
.
Повна енергія електромагнітного поля в контурі залишається постійною.
Потужність, яка виділяється на активному опорі контуру,
 . (2.121)
. (2.121)
Добротність контуру
 (2.122)
(2.122)
— величина, обернено пропорційна до відносної втрати енергії за період.
Затухання контуру
 . (2.123)
. (2.123)
Логарифмічний декремент затухання коливання
 (2.124)
(2.124)
— це натуральний логарифм відношення двох послідовних амплітуд через період.
 2017-10-25
2017-10-25 1079
1079








