Робота, потужність, енергія

Робота сталої сили ( = const)

, (1.35)

де — вектор переміщення; — кут між напрямами дії сили і переміщення.

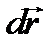При змінній силі, тобто , переміщення розбивають на елементарні переміщення такої величини, щоб в межах цього переміщення силу можна було вважати сталою. Тоді елементарна робота сили на переміщенні буде

. (1.36)

Повна робота, яка виконується змінною силою при переміщенні точки з положення 1 в положення 2,

. (1.37)

Середня потужність сили

. (1.38)

Миттєва потужність, тобто потужність у даний момент часу,

. (1.39)

Зв'язок потужності з діючою силою і швидкістю руху

, (1.40)

де кут між силою і швидкістю дорівнює .

Кінетична енергія матеріальної точки

, (1.41)

де — маса точки; — швидкість руху точки.

Приріст кінетичної енергії матеріальної точки

, (1.42)

де — робота результуючої всіх сил, що діють на матеріальну точку.

Потенціальна енергія тіла масою , піднятого над поверхнею планети на висоту

, (1.43)

де - прискорення вільного падіння на цій планеті.

Потенціальна енергія пружно деформованого тіла

, (1.44)

де - коефіцієнт жорсткості тіла; 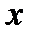- величина пружної деформації.

Зменшення потенціальної енергії матеріальної точки дорівнює роботі сил поля:

. (1.45)

Приріст повної механічної енергії матеріальної точки в потенціальному полі

, (1.46)

де — алгебраїчна сума робіт всіх сторонніх сил, що діють на тіло.

Закон зміни імпульсу системи

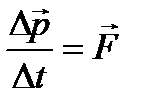, (1.47)

де — імпульс системи; — результуюча всіх зовнішніх сил.

У замкненій системі повний імпульс не змінюється (закон збереження імпульсу):

. (1.48)

Момент імпульсу матеріальної точки відносно деякого центра О

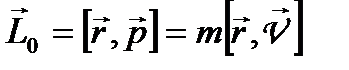, (1.49)

де — радіус-вектор, проведений з центра О до розглядуваної матеріальної точки;

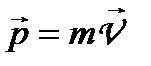— імпульс матеріальної точки.

Закон зміни моменту імпульсу системи

, (1.50)

де — сумарний момент всіх зовнішніх сил.

Закон збереження моменту імпульсу 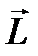замкнутої системи матеріальних точок

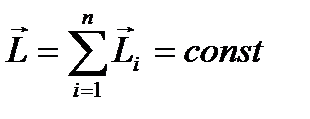. (1.51)

Момент сили 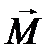відносно деякої точки О

, (1.52)

де — радіус-вектор, проведений з точки О в точку прикладання сили . Векторний добуток цих векторів можна написати у вигляді

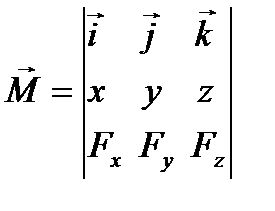, (1.53)

звідки значення складової, наприклад по вісі , дорівнює .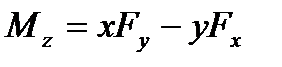

§ 4. Сили в механіці і сили інерції.

Механічна напруга сили , що діє на одиницю площі поперечного перерізу тіла

. (1.54)

Відношення абсолютної деформації (1.поперечної та поздовжньої ) до початкового розміру ( та ) називається відносна поперечна та поздовжня деформації

та . (1.55)

Відношення поперечної деформації до поздовжньої називається коефіцієнтом Пуасона

. (1.56)

Відносна зміна об'єму при поздовжній деформації

. (1.57)

Кут зсуву при деформації зсуву

, (1.58)

де 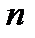- коефіцієнт зсуву; - дотична сила, яка викликає зсув; — дотична напруга; - модуль зсуву.

Модуль Юнга , модуль зсуву і коефіцієнт Пуассона 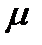зв'язані співвідношенням

. (1.59)

Кут закручення стержня

, (1.60)

де — обертальний момент; — довжина стержня; — радіус стержня.

Потенціальна енергія пружно деформованого стержня

, (1.61)

де — об'єм тіла.

Сила пружності

, (1.62)

де 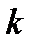- коефіцієнт пружності; - абсолютна деформація.

Потенціальна енергія деформованого пружного тіла

. (1.63)

Закон Гука

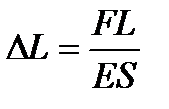, (1.64)

де - модуль пружності Юнга, Па.

Значення граничної зовнішньої сила тертя ковзання визначається за формулою Амонтона – Кулона:

, (1.65)

де - коефіцієнт тертя спокою; - сила нормального тиску.

Сила тертя кочення:

, (1.66)

де 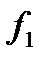- коефіцієнт тертя кочення, м; - радіус тіла, м.

Сила інерції, яка діє на рухоме тіло у системі відліку, що обертається має назву сила Коріоліса

, (1.67)

де - швидкість руху тіла масою , - кутова швидкість системи відліку.

§ 5. Динаміка обертального руху твердого тіла.

Основне рівняння динаміки обертального руху твердого тіла

, (1.68)

де — геометрична сума моментів зовнішніх сил; — момент інерції тіла; — кутове прискорення.

Момент інерції матеріальної точки масою , (1.69)

де — відстань від точки до центра обертання.

Момент інерції деяких тіл правильної геометричної форми

1) однорідної кулі масою і радіуса К відносно осі, що збігається з діаметром:

; (1.70)

2) однорідного стержня довжиною і масою відносно осі, що проходить через центр його мас перпендикулярно до осі стержня:

; (1.71)

3) однорідного диска (циліндра) радіуса і масою відносно осі, що збігається з віссю диска (циліндра):

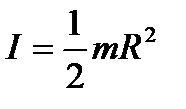; (1.72)

4) тонкостінного кільця (труби) радіуса масою відносно осі, що збігається з віссю кільця (труби):

; (1.73)

5) пустотілого циліндра масою відносно осі симетрії:

, (1.74)

де і — відповідно внутрішній і зовнішній радіуси циліндра.

Момент інерції тіла відносно будь-якої осі, що не проходить через центр мас тіла, визначається за теоремою Штейнера:

, (1.75)

де — момент інерції тіла відносно осі, яка паралельна даній і проведена через центр мас тіла; — відстань між осями.

Робота зовнішніх сил при повороті твердого тіла на кут

. (1.76)

У випадку змінного моменту зовнішніх сил

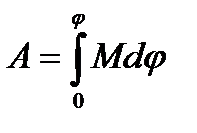. (1.77)

Кінетична енергія тіла, що обертається навколо нерухомої осі з кутовою швидкістю ,

, (1.78)

де — момент інерції тіла відносно розглядуваної осі обертання.

Якщо тіло одночасно перебуває у поступальному і обертальному рухах, то його кінетична енергія

, (1.79)

де і — відповідно кінетична енергія поступального і обертального рухів.

Момент імпульсу матеріальної точки відносно нерухомої точки

. (1.80)

Швидкість зміні з часом моменту імпульсу дорівнює моменту сили, що діє на тіло:

. (1.81)

Закон збереження моменту імпульсу в ізольованій механічній системі

. (1.82)

Момент імпульсу твердого тіла відносно нерухомої осі

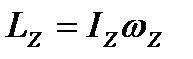, (1.83)

де — момент інерції тіла відносно нерухомої осі 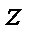; 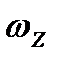— кутова швидкість обертання тіла навколо осі .

Кутова швидкість регулярної прецесії гіроскопа масою

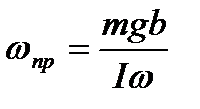, (1.84)

де - кутова швидкість гіроскопа; - його момент інерції; - відстань від точки опори до центра мас гіроскопа.