Опір послідовного контуру при вимушених коливаннях знаходиться за формулою (2.108)
Сила струму в контурі визначається за законом Ома.
Зсув фаз між струмом і напругою
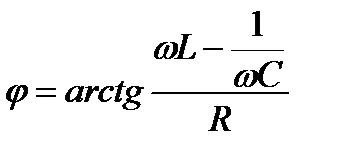 . (2.125)
. (2.125)
Миттєві значення напруги на конденсаторі і сили струму в контурі
 і
і  . (2.126)
. (2.126)
При резонансі
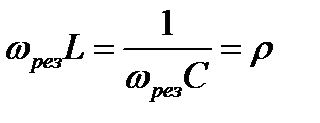 . (2.127)
. (2.127)
РОЗДІЛ 6. ОПТИКА
Тема 27. Геометрична оптика.
§§ 27.1 – 27.4
Закон заломлення світла
 , (3.1)
, (3.1)
де 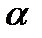 - кут падіння променя;
- кут падіння променя;  - кут заломлення променя;
- кут заломлення променя;  - відносний показник заломлення другого середовища відносно першого,
- відносний показник заломлення другого середовища відносно першого,  - швидкість і довжина світла у відповідному середовищі.
- швидкість і довжина світла у відповідному середовищі.
Під час повного внутрішнього відбивання, коли  , граничний кут пов'язаний рівнянням з відносним показником заломлення:
, граничний кут пов'язаний рівнянням з відносним показником заломлення:
 Рис. 34.1 Рис. 34.1 |
 . (3.2)
. (3.2)
Кут повороту проміння у тригранній призмі (див. рис. 34.1) входить до рівнянь
1). 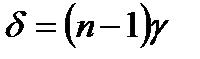 , якщо кут
, якщо кут  малий;
малий;
2).  при симетричному ході променя через призму;
при симетричному ході променя через призму;
3).  , якщо цей кут близький до 60о.
, якщо цей кут близький до 60о.
Формула сферичного дзеркала
 , (3.3)
, (3.3)
де  і
і  - відповідно відстані предмета і зображення від полюса дзеркала;
- відповідно відстані предмета і зображення від полюса дзеркала; 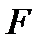 - фокусна відстань дзеркала;
- фокусна відстань дзеркала; 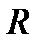 - радіус кривизни дзеркала. Для опуклого дзеркала
- радіус кривизни дзеркала. Для опуклого дзеркала  і
і  від’ємні.
від’ємні.
Формула тонкої лінзи
 , (3.4)
, (3.4)
де 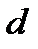 і
і 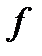 - відповідно відстані від оптичного центра лінзи до предмета і зображення;
- відповідно відстані від оптичного центра лінзи до предмета і зображення;  - відносний показник заломлення матеріалу лінзи;
- відносний показник заломлення матеріалу лінзи;  - фокусна відстань лінзи;
- фокусна відстань лінзи;  - оптична сила лінзи.
- оптична сила лінзи.
Лінійне збільшення дзеркала та лінзи
 , (3.5)
, (3.5)
де  і
і  - лінійні розміри зображення та предмета.
- лінійні розміри зображення та предмета.
Збільшення лупи:
 , (3.6)
, (3.6)
де 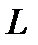 - відстань кращого зору.
- відстань кращого зору.
Збільшення мікроскопу і телескопу
 і
і  , (3.7)
, (3.7)
де  - відстань між окуляром і об’єктивом,
- відстань між окуляром і об’єктивом,  і
і  - фокусні відстані об’єктива та окуляра.
- фокусні відстані об’єктива та окуляра.
Оптична сила системи двох тонких лінз, складених до купи:
 . (3.8)
. (3.8)
ФОТОМЕТРІЯ
Освітленість  визначається світловим потоком
визначається світловим потоком 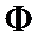 , що падає на одиницю площі
, що падає на одиницю площі
 . (3.9)
. (3.9)
Освітленість, яка створюється точковим ізотропним джерелом силою світла  , що знаходиться на відстані
, що знаходиться на відстані  ,
,
 , (3.10)
, (3.10)
де  - кут падіння променів.
- кут падіння променів.
Світність чисельно дорівнює світловому потоку, що випускається одиницею поверхні світного тіла:
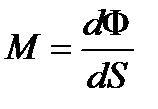 . (3.11)
. (3.11)
Яскравість 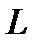 чисельно дорівнює відношенню сили світла з елемента випромінюючої поверхні до площі проекції цього елемента на площину, перпендикулярну до напряму спостереження:
чисельно дорівнює відношенню сили світла з елемента випромінюючої поверхні до площі проекції цього елемента на площину, перпендикулярну до напряму спостереження:
 , (3.12)
, (3.12)
де  - кут між нормаллю до елемента поверхні і напрямом спостереження.
- кут між нормаллю до елемента поверхні і напрямом спостереження.
Для ламбертівських джерел
 . (3.13)
. (3.13)
Експозиція визначається добутком освітленості і проміжку часу освітлення поверхні
 . (3.14)
. (3.14)
§ 28. ІНТЕРФЕРЕНЦІЯ СВІТЛА
Положення  та відстань між інтерференційними смугами
та відстань між інтерференційними смугами  на екрані, розміщеному паралельно двом когерентним джерелам світла,
на екрані, розміщеному паралельно двом когерентним джерелам світла,
 і
і  . (3.15)
. (3.15)
де  - довжина хвилі;
- довжина хвилі;  - відстань від екрана до джерел світла, розміщених на відстані
- відстань від екрана до джерел світла, розміщених на відстані  (при
(при  >
>  );
); 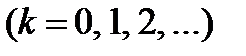 - порядок смуги на екрані.
- порядок смуги на екрані.
Результат інтерференції світла у плоскопаралельних пластинках, що знаходяться у повітрі (в прохідному світлі), визначається формулами:
підсилення світла
 ,
, 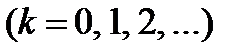 ; (3.16)
; (3.16)
послаблення світла
 ,
,  , (3.17)
, (3.17)
де 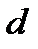 - товщина пластинки;
- товщина пластинки;  - показник заломлення;
- показник заломлення;  - кут заломлення;
- кут заломлення; 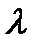 - довжина хвилі світла.
- довжина хвилі світла.
У відбитому світлі умови підсилення і ослаблення світла обернені умовам у прохідному світлі.
Радіуси світлих кілець Ньютона (у прохідному світлі) визначаються формулою
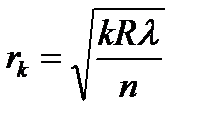
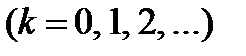 ; (3.18)
; (3.18)
радіуси темних кілець
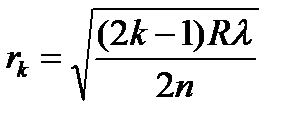
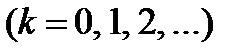 , (3.19)
, (3.19)
де  - радіус кривизни лінзи,
- радіус кривизни лінзи, 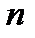 - показник заломлення середовища, яке заповнює простір між лінзою та пластиною. У відбитому світлі розміщення світлих і темних кілець обернене їхньому розміщенню у прохідному світлі.
- показник заломлення середовища, яке заповнює простір між лінзою та пластиною. У відбитому світлі розміщення світлих і темних кілець обернене їхньому розміщенню у прохідному світлі.
§ 29. ДИФРАКЦІЯ СВІТЛА
Радіус  -ї зони Френзеля для сферичного фронту хвилі дорівнює (див. рис. 29.1):
-ї зони Френзеля для сферичного фронту хвилі дорівнює (див. рис. 29.1):
 , (3.20)
, (3.20)
де  - радіус фронту сферичної хвилі;
- радіус фронту сферичної хвилі; 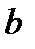 - відстань від точки спостерігання до фронту хвилі;
- відстань від точки спостерігання до фронту хвилі; 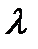 - довжина хвилі;
- довжина хвилі;  .
.
Площа зони Френзеля для сферичної хвилі (при малих 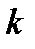 ) дорівнює
) дорівнює
 . (3.21)
. (3.21)
Положення мінімумів освітленості при дифракції від щілини, на яку нормально падає пучок паралельних променів,
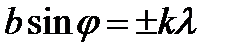
 , (3.22)
, (3.22)
де  - ширина щілини;
- ширина щілини;  - кут дифракції;
- кут дифракції;  - довжина хвилі падаючого світла.
- довжина хвилі падаючого світла.
У дифракційній решітці максимуми світла спостерігаються в напрямах, які складають з нормаллю до решітки кут  , що задовольняє умові
, що задовольняє умові 
 при нормальному падінні світла на решітку, де
при нормальному падінні світла на решітку, де  -стала решітки;
-стала решітки;  - кут дифракції;
- кут дифракції;  - довжина хвилі падаючого світла;
- довжина хвилі падаючого світла;  - порядок спектра.
- порядок спектра.
Роздільна здатність дифракційної решітки визначається за формулою
 , (3.23)
, (3.23)
де 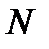 - загальна кількість штрихів решітки;
- загальна кількість штрихів решітки;  - порядок спектра;
- порядок спектра; 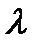 і
і 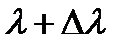 - довжини найближчих спектральних ліній, які ще розрізняються решіткою.
- довжини найближчих спектральних ліній, які ще розрізняються решіткою.
Кутовою дисперсією дифракційної решітки є величина
 . (3.24)
. (3.24)
Лінійною дисперсією дифракційної решітки для малих кутів дифракції є величина
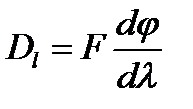 , (3.25)
, (3.25)
 Рис. 29.1 Рис. 29.1 |
де  - фокусна відстань лінзи, що проектує спектр на екран;
- фокусна відстань лінзи, що проектує спектр на екран;  - кутова відстань між спектральними лініями, що відрізняються за довжиною хвилі на
- кутова відстань між спектральними лініями, що відрізняються за довжиною хвилі на  .
.
Формула Вульфа — Брегга
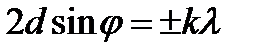 , (3.26)
, (3.26)
де  —відстань між атомними площинами кристала;
—відстань між атомними площинами кристала; 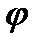 - кут ковзання променів;
- кут ковзання променів;  - порядок спектра.
- порядок спектра.
§ 30. ПОЛЯРИЗАЦІЯ СВІТЛА. РОЗСІЯННЯ, ПОГЛИНАННЯ, ДИСПЕРСІЯ СВІТЛА
При відбиванні природного світла від діелектрика мають місце формули Френзеля:
 ,
,
 , (3.27)
, (3.27)
де  - інтенсивність падаючого природного світла;
- інтенсивність падаючого природного світла;  - інтенсивність відбитого світла, у якого коливання вектору напруженості
- інтенсивність відбитого світла, у якого коливання вектору напруженості  світлової хвилі перпендикулярні площині падіння;
світлової хвилі перпендикулярні площині падіння;  - інтенсивність відбитого світла, у якого коливання вектору напруженості
- інтенсивність відбитого світла, у якого коливання вектору напруженості  світлової хвилі паралельні площині падіння;
світлової хвилі паралельні площині падіння;  ,
,  - відповідно кути падіння та заломлення світла.
- відповідно кути падіння та заломлення світла.
Коефіцієнт відбивання даної поверхні дорівнює:
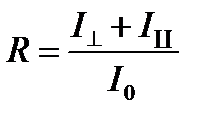 , (3.28)
, (3.28)
для малих кутів падіння
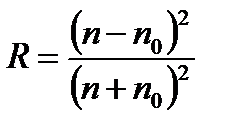 , (3.29)
, (3.29)
де  - показник заломлення середовища, в якому розповсюджується світло;
- показник заломлення середовища, в якому розповсюджується світло;  - показник заломлення середовища, від поверхні якого світло відбивається.
- показник заломлення середовища, від поверхні якого світло відбивається.
При відбиванні світла від діелектрика повна поляризація відбитого променя відбувається при умові (закон Брюстера)
 , (3.30)
, (3.30)
де 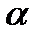 - кут падіння променів;
- кут падіння променів; 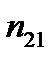 - відносний показник заломлення.
- відносний показник заломлення.
Інтенсивність світла, що проходить крізь поляризатор і аналізатор (закон Малюса),
 , (3.31)
, (3.31)
де  - кут між головними площинами поляризатора й аналізатора;
- кут між головними площинами поляризатора й аналізатора;  - інтенсивність світла, що пройшло крізь поляризатор.
- інтенсивність світла, що пройшло крізь поляризатор.
Кут повороту площини поляризації оптично активною речовиною 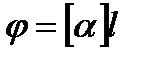 , де
, де  - стала обертання, що залежить від природи речовини і довжини світлової хвилі;
- стала обертання, що залежить від природи речовини і довжини світлової хвилі; 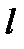 - відстань, яку пройшов світловий промінь у речовині. Для розчинів
- відстань, яку пройшов світловий промінь у речовині. Для розчинів  , де
, де  - концентрація речовини у розчині;
- концентрація речовини у розчині;  - питоме повертання.
- питоме повертання.
Інтенсивність світла, розсіяного речовиною, залежить ві довжини хвилі (закон Релея):
 , (3.32)
, (3.32)
де 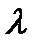 - довжина світлової хвилі.
- довжина світлової хвилі.
Інтенсивність світла, розсіяного під кутом  до напряму опромінювання (індикатриса розсіяння),
до напряму опромінювання (індикатриса розсіяння),
 , (3.33)
, (3.33)
де  - інтенсивність світла розсіяного під прямим кутом.
- інтенсивність світла розсіяного під прямим кутом.
Швидкість поширення світла в ізотропному середовищі з показником заломлення п
 , (3.34)
, (3.34)
де  - абсолютна електрична проникність середовища
- абсолютна електрична проникність середовища  ;
;  - абсолютна магнітна проникність середовища
- абсолютна магнітна проникність середовища  ;
;  - швидкість світла у вакуумі.
- швидкість світла у вакуумі.
Закон Бугера
 , (3.35)
, (3.35)
де 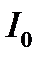 - інтенсивність світла, яке падає на речовину;
- інтенсивність світла, яке падає на речовину;  - інтенсивність світла, що пройшло крізь шар речовини товщиною
- інтенсивність світла, що пройшло крізь шар речовини товщиною  ;
;  - коефіцієнт поглинання.
- коефіцієнт поглинання.
Для поглинання світла в розчинах виконується закон Бугера – Ламберта:
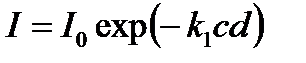 , (3.36)
, (3.36)
де  - коефіцієнт поглинання на одиницю концентрації речовини;
- коефіцієнт поглинання на одиницю концентрації речовини;  - концентрація розчину речовини.
- концентрація розчину речовини.
Оптична густина розчину:
 . (3.37)
. (3.37)
Зменшення інтенсивності світла в наслідок розсіювання:
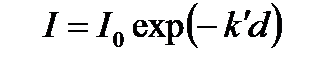 , (3.38)
, (3.38)
де  - коефіцієнт розсіювання. Сумісна дія поглинання та розсіювання зводить до зміни інтенсивності по закону:
- коефіцієнт розсіювання. Сумісна дія поглинання та розсіювання зводить до зміни інтенсивності по закону:
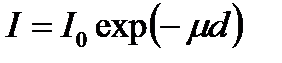 , (3.39)
, (3.39)
де  .
.
Залежність показника заломлення речовини п від частоти падаючої світлової хвилі
 , (3.40)
, (3.40)
де  - електрична стала;
- електрична стала;  ,
,  - заряд і маса електрона;
- заряд і маса електрона; 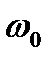 - власна циклічна частота коливань електронів середовища;
- власна циклічна частота коливань електронів середовища;  - концентрація електронів.
- концентрація електронів.
Коефіцієнт відбивання речовини при врахуванні поглинання
 , (3.41)
, (3.41)
де  - головний показник поглинання.
- головний показник поглинання.
Випромінювання Вавілова - Черенкова: кут між напрямом поширення випромінювання і вектором швидкості частинки
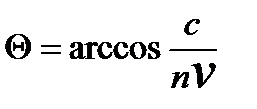 , (3.42)
, (3.42)
де  - швидкість частинки.
- швидкість частинки.
РЕЛЯТИВІСТСЬКІ ЕФЕКТИ В ОПТИЦІ
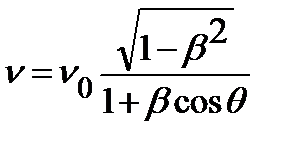 , (3.43)
, (3.43)
де 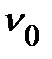 — частота коливань хвиль джерела;
— частота коливань хвиль джерела; 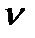 — частота, яку сприймає спостерігач при наближенні (віддаленні) джерела;
— частота, яку сприймає спостерігач при наближенні (віддаленні) джерела;  ;
; 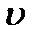 —відносна швидкість джерела відносно спостерігача;
—відносна швидкість джерела відносно спостерігача;  — кут між напрямом швидкості
— кут між напрямом швидкості  і напрямом спостереження в системі, зв'язаній з спостерігачем.
і напрямом спостереження в системі, зв'язаній з спостерігачем.
Теорема додавання швидкостей
 , (3.44)
, (3.44)
де  — відносна;
— відносна;  — переносна;
— переносна;  — абсолютна швидкості.
— абсолютна швидкості.
§ 31 - 32. КВАНТОВІ ВЛАСТИВОСТІ ВИПРОМІНЮВАННЯ
Енергетична світність абсолютно чорного тіла
 , (3.45)
, (3.45)
де  — абсолютна температура;
— абсолютна температура;  = 5,67•10-8 Вт/(м2 К4) — стала Стефана - Больцмана.
= 5,67•10-8 Вт/(м2 К4) — стала Стефана - Больцмана.
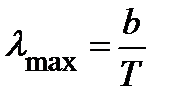 , (3.46)
, (3.46)
де 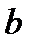 = 2,89•10-3м•К — стала Віна;
= 2,89•10-3м•К — стала Віна;  — довжина хвилі, на яку припадає максимум випромінювальної здатності.
— довжина хвилі, на яку припадає максимум випромінювальної здатності.
 , (3.47)
, (3.47)
де  = 6,626•10-34 Дж*с — стала Планка;
= 6,626•10-34 Дж*с — стала Планка; 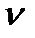 — частота.
— частота.
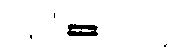
 . (3.48)
. (3.48)
Імпульс і маса фотона
 , (3.49)
, (3.49)
де с — швидкість поширення світла у вакуумі.
Рівняння Ейнштейна для зовнішнього фотоефекту
 , (3.50)
, (3.50)
де  — робота виходу електрона;
— робота виходу електрона; 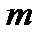 — маса електрона;
— маса електрона;  — максимальна швидкість електронів.
— максимальна швидкість електронів.
Тиск світла
 , (3.51)
, (3.51)
де  — енергія, що припадає на одиницю площі за одиницю часу;
— енергія, що припадає на одиницю площі за одиницю часу;  — коефіцієнт відбивання світла.
— коефіцієнт відбивання світла.
 , (3.52)
, (3.52)
де 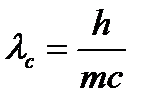 - комптонівська довжина хвилі,
- комптонівська довжина хвилі,  - кут розсіювання.
- кут розсіювання.
Інтенсивність пучка рентгенівських променів під час проходження їх через поглинаюче середовище:
 , (3.53)
, (3.53)
де  - інтенсивність рентгенівських променів, що падають на поверхню речовини,
- інтенсивність рентгенівських променів, що падають на поверхню речовини,  - лінійний коефіцієнт поглинання,
- лінійний коефіцієнт поглинання, 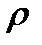 - густина речовини,
- густина речовини,  - масовий коефіцієнт поглинання.
- масовий коефіцієнт поглинання.
§ 33. ХВИЛЬОВІ ВЛАСТИВОСТІ РЕЧОВИНИ
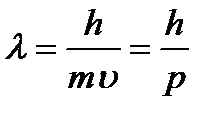 , де
, де  . (3.54)
. (3.54)
Співвідношення невизначеностей Гейзенберга
 , (3.55)
, (3.55)
де  — невизначеність проекції імпульсу частинки на вісь х;
— невизначеність проекції імпульсу частинки на вісь х;  — невизначеність координати частинки;
— невизначеність координати частинки;  —невизначеність енергії даного квантового стану;
—невизначеність енергії даного квантового стану;  — час перебування частинки у даному енергетичному стані.
— час перебування частинки у даному енергетичному стані.
Співвідношення між повною енергією  та імпульсом релятивістської частинки з масою спокою
та імпульсом релятивістської частинки з масою спокою 
 . (3.56)
. (3.56)
Рівняння Шредінгера для стаціонарних станів
 , (3.57)
, (3.57)
де  - повна енергія частинки;
- повна енергія частинки;  - потенціальна енергія частинки.
- потенціальна енергія частинки.
Хвильова функція задовольняє умові нормировки:
 . (3.58)
. (3.58)
Власна функція квантової частинки, що рухається в одномірній прямокутній ямі має вигляд
 , (3.59)
, (3.59)
де 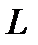 - ширина ями.
- ширина ями.
Імовірність знаходження частинки в об’ємі 
 , (3.60)
, (3.60)
де  - густина імовірності.
- густина імовірності.
Коефіцієнт відбивання хвиль де Бройля від низького потенційного бар’єру нескінченної ширини
 , (3.61)
, (3.61)
де  - хвильове число у відповідних областях простору.
- хвильове число у відповідних областях простору.
Коефіцієнт прозорості потенціального бар'єру 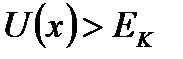
 . (3.62)
. (3.62)
Відносна густина імовірності знаходження частинки за бар’єром у цьому випадку дорівнює
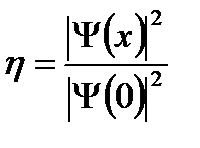 , (3.63)
, (3.63)
де хвильова функція в цьому випадку дорівнює
 , (3.64)
, (3.64)
де  - стала.
- стала.
§ 34. БУДОВА АТОМІВ І МОЛЕКУЛ
Кут розсіяння альфа-частинки кулонівським полем нерухомого ядра
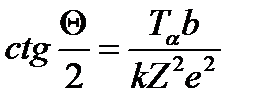 , (3.65)
, (3.65)
де  — кінетична енергія альфа-частинки;
— кінетична енергія альфа-частинки; 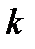 = 9•109 м/Ф; е — заряд ядра атома.
= 9•109 м/Ф; е — заряд ядра атома.
Формула Резерфорда. Відносна кількість частинок, розсіяних в елементарному тілесному куті сій під кутом 0 до початкового напряму руху,
 , (3.66)
, (3.66)
де  — число ядер мішені на одиницю її поверхні;
— число ядер мішені на одиницю її поверхні;
 . (3.67)
. (3.67)
Узагальнена формула Бальмера для воднеподібних іонів
 , (3.68)
, (3.68)
де 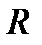 = 10973731,53 м-1- стала Ридберга,
= 10973731,53 м-1- стала Ридберга,  - довжина хвилі фотона;
- довжина хвилі фотона;  - заряд ядра у відносних одиницях (при
- заряд ядра у відносних одиницях (при 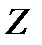 = 1 формула переходить у серіальну формулу для водню);
= 1 формула переходить у серіальну формулу для водню); 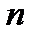 - номер орбіти, на яку перейшов електрон;
- номер орбіти, на яку перейшов електрон;  -номер орбіти, з якої перейшов електрон (
-номер орбіти, з якої перейшов електрон (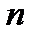 і
і  - головні квантові числа).
- головні квантові числа).
Серії ліній спектра водню:  = 1 – серія Лаймана (амер.ф. 1874-1954),
= 1 – серія Лаймана (амер.ф. 1874-1954), 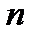 = 2 – серія Бальмера (шкейц.ф. 1825-1898),
= 2 – серія Бальмера (шкейц.ф. 1825-1898), 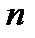 = 3 – серія Па шена (н.ф. 1865-1947),
= 3 – серія Па шена (н.ф. 1865-1947),  = 4 – серія Брекета,
= 4 – серія Брекета, 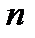 = 5 – серія Пфунда (амер.ф. 1879-1949),
= 5 – серія Пфунда (амер.ф. 1879-1949),  = 6 – серія Хемфрі.
= 6 – серія Хемфрі.
Модуль моменту імпульсу
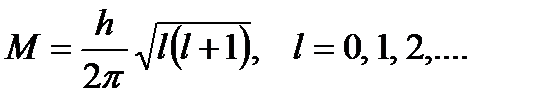 (3.69)
(3.69)
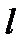 — азимутальне квантове число; проекція вектора моменту імпульсу на обраний напрям
— азимутальне квантове число; проекція вектора моменту імпульсу на обраний напрям
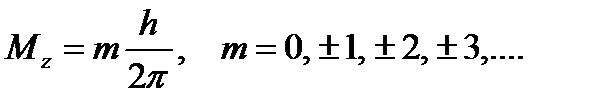 (3.70)
(3.70)
 - магнітне квантове число.
- магнітне квантове число.
Кратність виродження рівнів водню
 , (3.71)
, (3.71)
де  — головне квантове число.
— головне квантове число.
Правила відбору
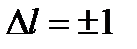 . (3.72)
. (3.72)
Момент імпульсу електрона, який рухається навколо ядра (перший постулат Бора)
 , (3.73)
, (3.73)
де  - маса електрона,
- маса електрона,  - його швидкість на
- його швидкість на  -й орбіті,
-й орбіті,  - радіус цієї орбіти,
- радіус цієї орбіти,  — головне квантове число.
— головне квантове число.
Другий постулат Бора
 , (3.74)
, (3.74)
де  - енергія електрона на відповідних орбітах.
- енергія електрона на відповідних орбітах.
Дозволені значення внутрішньої енергії водню подібного атому:
 . (3.75)
. (3.75)
Узагальнена формула закону Мозлі
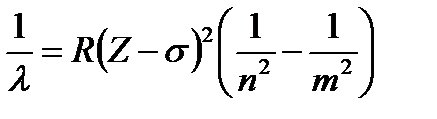 , (3.76)
, (3.76)
де 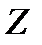 — заряд ядра;
— заряд ядра;  — стала екранування (для К-серії
— стала екранування (для К-серії  = 0,97).
= 0,97).
Під час дифракції рентгенівських променів має місце рівняння Вульфа-Брегга
 , (3.77)
, (3.77)
де  - відстань між атомними площинами кристалу,
- відстань між атомними площинами кристалу,  - кут між пучком рентгенівських променів і поверхнею кристалу.
- кут між пучком рентгенівських променів і поверхнею кристалу.
Короткохвильова границя суцільного рентгенівського спектру може бути знайденою за формулою
 , (3.78)
, (3.78)
де  - різниця потенціалів, яка прикладена до рентгенівської трубки.
- різниця потенціалів, яка прикладена до рентгенівської трубки.
§ 35. КВАНТОВІ ЯВИЩА В ТВЕРДИХ ТІЛАХ
Функція розподілу ферміонів за енергіями
 . (3.79)
. (3.79)
Енергія Фермі
 . (3.80)
. (3.80)
Середнє значення енергії вільного електрона
 . (3.81)
. (3.81)
Теплоємність електронного газу
 , (3.82)
, (3.82)
де  — концентрація вільних електронів.
— концентрація вільних електронів.
Характеристична температура Дебая
 ,
, 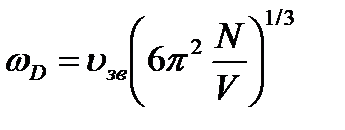 , (3.83)
, (3.83)
де  — швидкість поширення звуку;
— швидкість поширення звуку; 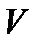 — об'єм зразка;
— об'єм зразка;  — кількістб електронів,
— кількістб електронів, 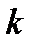 - стала Больцмана.
- стала Больцмана.
Розподіл Фермі — Дірака — концентрація вільних електронів з енергіями 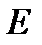 ,
, 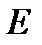 +
+ 
 .(3.84)
.(3.84)
Питома електропровідність чистих напівпровідників
 . (3.85)
. (3.85)
Стала Холла для напівпровідників із змішаним типом провідності
 , (3.86)
, (3.86)
де  ,
, 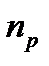 — концентрації електронів та дірок;
— концентрації електронів та дірок;  ,
,  —рухливості електронів та дірок.
—рухливості електронів та дірок.
Питома електропровідність металів
 , (3.87)
, (3.87)
де 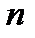 - концентрація вільних електронів,
- концентрація вільних електронів,  - елементарний заряд,
- елементарний заряд, 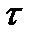 - час релаксації,
- час релаксації,  - маса електрона.
- маса електрона.
Рухливість носіїв току:
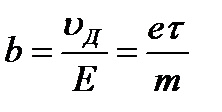 , (3.88)
, (3.88)
де  - швидкість дрейфу носіїв току,
- швидкість дрейфу носіїв току, 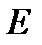 - напруженість електричного полю.
- напруженість електричного полю.
Молярна теплоємність кристалу в квантовій теорії теплоємності Ейнштейна:
 , (3.89)
, (3.89)
де  - молярна газова стала,
- молярна газова стала,  - характеристична температура Ейнштейна.
- характеристична температура Ейнштейна.
Молярна внутрішня енергія кристалу по Дебаю:
 , (3.90)
, (3.90)
де  - молярна енергія нульових коливань кристалу по Дебаю,
- молярна енергія нульових коливань кристалу по Дебаю,  =
= 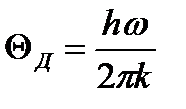 - характеристична температура Дебая.
- характеристична температура Дебая.
Молярна теплоємність кристала по Дебаю:
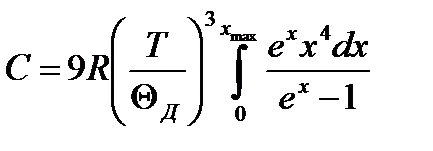 , (3.91)
, (3.91)
де  - змінна.
- змінна.
У інтервалі низьких температур, тобто при умові  , молярна теплоємність кристалічного твердого тіла дорівнює
, молярна теплоємність кристалічного твердого тіла дорівнює
 . (3.91а)
. (3.91а)
§ 38. ОСНОВНІ ХАРАКТЕРИСТИКИ АТОМНОГО ЯДРА
Розмір ядра з масовим числом А
 м. (3.92)
м. (3.92)
Енергія зв'язку ядра
 , (3.93)
, (3.93)
де  — заряд ядра;
— заряд ядра;  — масове число;
— масове число; 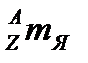 — маса ядра;
— маса ядра;  — маса протона, маса атома водню,
— маса протона, маса атома водню,  — маса нейтрона.
— маса нейтрона.
Якщо взяти не масу ядра, а масу атома  і замість маси протона записати масу атома водню
і замість маси протона записати масу атома водню 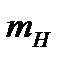 , то дефект маси ядра можна підрахувати за формулою
, то дефект маси ядра можна підрахувати за формулою
 . (3.94)
. (3.94)
Магнітний момент ядра
 , (3.95)
, (3.95)
де  - гіромагнітний множник;
- гіромагнітний множник;  — спін ядра;
— спін ядра;  = 5,05*10-27Дж • Тл-1 — ядерний магнетон.
= 5,05*10-27Дж • Тл-1 — ядерний магнетон.
§ 39. РАДІОАКТИВНІСТЬ
Кількість ядер, які ще не розпались за час t
 , (3.96)
, (3.96)
де 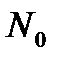 — кількість ядер у початковий момент;
— кількість ядер у початковий момент;  — стала розпаду,
— стала розпаду,  — період піврозпаду.
— період піврозпаду.
Середній час життя радіоактивного ядра
 . (3.97)
. (3.97)
Активність препарату
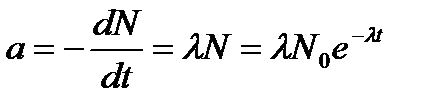 . (3.98)
. (3.98)
Якщо радіоізотоп  з постійною розпаду
з постійною розпаду  перетворюється в радіоізотоп
перетворюється в радіоізотоп  з постійною розпаду
з постійною розпаду  ,то кількість ядер радіоізотопу
,то кількість ядер радіоізотопу  змінюється з часом згідно закону
змінюється з часом згідно закону
 , (3.99)
, (3.99)
де  - кількість ядер радіоізотопу
- кількість ядер радіоізотопу  в момент часу
в момент часу  .
.
Вікове рівняння
 . (3.100)
. (3.100)
Контрольна робота №1
1. Матеріальна точка рухається прямолінійно. Залежність пройденого шляху від часу описується рівнянням S = (8,5 + 5t + t3) м. Визначити середню швидкість точки за 2,5 секунд руху.
2. Матеріальна частинка рухається з прискоренням  . Визначити модуль швидкості частинки в момент часу t = 0,1 с, якщо в початковий момент часу t = 0 її швидкість дорівнювала
. Визначити модуль швидкості частинки в момент часу t = 0,1 с, якщо в початковий момент часу t = 0 її швидкість дорівнювала 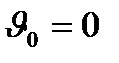 .
.
3. Аеростат піднімається вгору із швидкістю 1 м/с. У момент, коли він знаходився на висоті 100 м, з нього випав камінь. Знайти час, за який камінь досягне поверхні Землі.
4. Камінь кинули з вишки у горизонтальному напрямі з швидкістю 20 м/с. Визначити радіус кривизни траєкторії каменя в кінці 0,2 секунди після початку руху.
5. Диск радіуса 10 см, що знаходився у стані спокою, почав обертатися із сталим кутовим прискоренням  . Знайти повне прискорення точок на ободі диска в кінці першої секунди після початку руху.
. Знайти повне прискорення точок на ободі диска в кінці першої секунди після початку руху.
6. Рух матеріальної точки задано рівнянням 
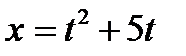 , м. Визначити швидкість точки в кінці 1 секунди руху.
, м. Визначити швидкість точки в кінці 1 секунди руху.
7. На висоті 100 м тіло, що вільно падає, мало швидкість 40 м/с Чому дорівнювала швидкість тіла на висоті 61 м/с?
8. Положення тіла задається радіусом-вектором  . Знайти швидкість тіла в момент часу t = 1 с.
. Знайти швидкість тіла в момент часу t = 1 с.
9. Знайти нормальне і тангенціальне прискорення тіла, яке кинуто з початковою швидкістю 10 м/с під кутом 31° до горизонту, через 0,3 с польоту.
10. Колесо радіуса 0,1 м обертається так, що залежність кута повороту радіуса колеса від часу описується рівнянням 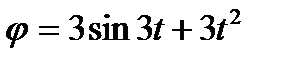 . Для точок на ободі колеса знайти через
. Для точок на ободі колеса знайти через  с після початку руху лінійну швидкість.
с після початку руху лінійну швидкість.
11. Швидкість тіла змінюється за законом  ,м/с. Знайти прискорення тіла через 2 с руху.
,м/с. Знайти прискорення тіла через 2 с руху.
12. Тіло починає падати з висоти 100 м з прискоренням 9,81 м/с2вздовж вертикалі і з прискоренням 4.9 м/с2рухатись вздовж горизонталі. Знайти швидкість тіла через 0,1 с після початку цього польоту.
13. Тіло кинуто з поверхні землі під кутом 45° до горизонту з початковою швидкістю 10 м/с. Не враховуючи опору повітря, знайти далекість польоту.
14. Частинка рухається згідно з рівняннями  . Знайти модуль переміщення частинки за першу секунду руху.
. Знайти модуль переміщення частинки за першу секунду руху.
15. Диск радіуса 1 см обертається згідно з рівнянням 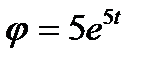 . Визначити повне прискоренняточок краю диска для моменту часу t = 0,2 с.
. Визначити повне прискоренняточок краю диска для моменту часу t = 0,2 с.
16. Першу чверть шляху мотоцикліст проїхав зі швидкістю 10м/с, другу зі швидкістю 15 м/с, третю зі швидкістю 20 м/с й останню зі швидкістю 1 м/с. Визначити середню швидкість.
17. Рух матеріальної точки задано рівнянням;  , м. Визначити середню швидкість її руху в інтервалі часу від 2 с до 4 с.
, м. Визначити середню швидкість її руху в інтервалі часу від 2 с до 4 с.
18. Рух матеріальної точки задано рівняннями:  , м. Визначити модуль її швидкості в момент часу t = 1 с.
, м. Визначити модуль її швидкості в момент часу t = 1 с.
19. Тіло кинуте в горизонтальному напрямку зі швидкістю 1 м/с. Визначити нормальне прискорення тіла через 2 с після початку руху.
20. Визначити кутову швидкість твердого тіла, що обертається навколо нерухомої осі за законом  , рад., у момент часу t = 1 с.
, рад., у момент часу t = 1 с.
21. Тіло кинуте зі швидкістю 10 м/с під кутом 45° до обрію. Знайти радіус кривизни траєкторії тіла через 1 с після початку руху.
22. З вежі висотою 25 м кинули камінь зі швидкістю 15 м/с під кутом 30° до обрію. Визначити як далеко камінь полетить від вежі.
23. Колесо, через 1 хв після початку обертання, здобуває швидкість, що відповідає частоті 30 оберт/хв. Знайти число оборотів колеса за цю хвилину. Рух уважати рівноприскоренним.
24. Точка рухається по окружності радіусом 10 см з постійним тангенціальним прискоренням. Знайти нормальне прискорення її через 20 с після початку руху, якщо відомо, що до кінця п'ятого обороту після початку руху її лінійна швидкість дорівнює 1 см/с.
25. Колесо радіусом 1 см обертається так, що залежність кута повороту радіуса колеса від часу задано рівнянням 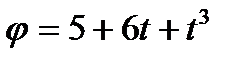 . Знайти для точок, що лежать на обіді колеса, зміну тангенціального прискорення за кожну секунду руху.
. Знайти для точок, що лежать на обіді колеса, зміну тангенціального прискорення за кожну секунду руху.
26. Камінь кинутий горизонтально зі швидкістю 10 м/с Знайти радіус кривизни траєкторії каменю через 3 с від початку руху.
27. Камінь, кинутий зі швидкістю 10 м/с під кутом 45° до обрію, упав на землю на деякій відстані від місця кидання. З якої висоти треба кинути камінь у горизонтальному напрямку, щоб при тій же початковій швидкості він упав на те ж місце?
28. Знайти радіус обертового колеса, якщо відомо, що лінійна швидкість точки, що лежить на обіді, в 2,5 рази більше лінійної швидкості точки, що лежить на 1 см ближче до осі колеса.
29. Точка рухається по окружності радіусом 20 см з постійним тангенціальним прискоренням 1 см/с. Через який час після початку руху її нормальне прискорення буде дорівнювати тангенціальному?
30. Точка рухається по окружності так, що залежність шляху від часу дається в рівнянням  . Знайти повне прискорення її через 3 с з початку руху, якщо відомо, що її нормальне прискорення через 2 с дорівнює 1 м/с.
. Знайти повне прискорення її через 3 с з початку руху, якщо відомо, що її нормальне прискорення через 2 с дорівнює 1 м/с.
Динаміка.
1. Наскільки необхідно зменшити масу аеростату, що рівномірно опускається, щоб він почав рівномірно підніматися з тією же швидкістю? Маса аеростату з баластом 1210 кг, а піднімальна сила 12000 Н. Силу опору повітря руху аеростата вважати однакової при підйомі й при спуску.
2. Автомобіль масою 103 кг зупиняється при гальмуванні за 5 с, пройшовши відстань в 10 м. Знайти силу гальмування.
3. Тіло масою 10 кг рухається прямолінійно, причому залежність пройденого шляху від часу дається рівнянням  , знайти величину сили, що діє на тіло наприкінці першої секунди руху.
, знайти величину сили, що діє на тіло наприкінці першої секунди руху.
4. Тїло сковзає по похилій площині, що становить із обрієм кут 35°. Пройшовши відстань 50 см, тіло здобуває швидкість 2 м/с. Чому дорівнює коефіцієнт тертя тіла об площину?
5. Дві гирі 10 кг й 5 кг з'єднані ниткою й перекинуті через невагомий блок. Знайти натяг нитки в процесі руху гир. Тертям у блоці знехтувати.
6. Чому дорівнює діюча на тіло сила через 10 с від початку руху, якщо його рух описується рівнянням 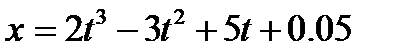 ? Маса тіла 0,1 кг.
? Маса тіла 0,1 кг.
7. Визначити коефіцієнт тертя між похилою площиною й тілом, що рухається по ній, якщо відомо, що це тіло, маючи початкову швидкість 5 м/с і рухаючись нагору по похилій площині, проходить шлях 2 м. Кут нахилу площини 12 градусів.
8. М'яч масою 100 м летить горизонтально з деякою швидкістю й ударяється об нерухому стіну. За час 0,01 с він стискується на 1,37 см. Стільки ж часу він відновлює свою форму. Знайти середню силу, що діє на стіну за час удару.
9. Тіло масою 10 кг рухається зі швидкістю 1 м/с уздовж радіуса горизонтальної платформи, що обертається із частотою 60 1/хв. Визначити діючу на тіло силу Коріолиса.
10. Камінь, прив'язаний до мотузки, рівномірно обертається у вертикальній площині. Знайти масу каменю, якщо відомо, що різниця між максимальним і мінімальним натягом мотузки дорівнює 10 Н.
11. Під дією деякої сили тіло масою 5 кг знаходиться у прямолінійному русі, який описується рівнянням.  . Чому дорівнює сила, що діє на тіло в момент часу t = 5 с?
. Чому дорівнює сила, що діє на тіло в момент часу t = 5 с?
12. Вагон масою 104 кг відчепився від потягу, що рухається, і, рухаючись рівномірноуповільнено, за 100 с пройшов шлях 20 м, після чого зупинився. Знайти коефіцієнт тертя.
13. Яку максимальну силу необхідно розвити при натягу лука на 20 см, якщо вся робота, яку виконано, йде на збільшення кінетичної енергії стріли, а найбільша дальність польоту стріли 35 м? Маса стріли 50 г.
14. По горизонтальній ділянці дороги їде велосипедист, описуючи дугу радіусом 5 м. Під яким кутом до обрію нахилений велосипедист, якщо його швидкість 6 м/с?
15. Нейтрон ударяється об нерухоме ядро атома, маса якого в 5 раз більше маси нейтрона. Уважаючи удар центральним і пружним, знайти, яку частину своєї швидкості втратить нейтрон при ударі.
16. Чему равна кинетическая энергия тела массой 25 г через 5 с от начала движения, если оно описывается уравнением  .
.
17. Чему равен коэффициент трения колеса автомобиля о дорогу, если при скорости 10 м/с тормозной путь равен 25 м?
18. Стальная проволока длиной 250 м поднимается вертикально вверх под действием силы, приложенной к ее верхнему концу. При каком ускорении наступит разрыв проволоки? Предел прочности стали 0,69 ГПа? Плотность стали 6,9*103 кг/м3
19. На наклонной плоскости с углом наклона 30о лежит тело. Наклонная плоскость движется с ускорением 1 м/с2, направленном горизонтально. Чему равно значение коэффициента трения, если тело не соскальзывает с наклонное плоскости? Рассмотреть два случая.
20. Шарик из пластмассы, падая с высоты 1 м, несколько раз отскакивает от пола. Чему равен коэффициент восстановления при ударе шарика о пол, если с момента падения до второго удара о пол прошло 1,3 с?
21. К нити подвешена гиря. Если поднимать эту гирю с ускорением 5 м/с2натяжение нити будет вдвое меньшетого натяжения, при котором нить разрывается. С каким ускорением надо поднимать эту гирю, чтобы нить разорвалась?
22. Поезд весом 4,9*106Н после прекращения тяги локомотива под действием силы трения в 9,8*104останавливается в течение 5 с. С какой скоростью шел поезд?
23. Тело весом 5 Н движется прямолинейно, причем зависимость пройденного пути от времени дается уравнением  . Найти величину силы, действующую на тело в конце первой секунды.
. Найти величину силы, действующую на тело в конце первой секунды.
24. Два тела движутся навстречу друг другу и ударяются не упруго. Скорость первого тела до удара равна 2 м/с, скорость второго 5 м/с. Общая скорость тел после удара по направлению совпадает с направлением скорости первого тела и равна 1 м/с. Найти отношение кинетическая энергия первого тела к кинетической энергии второго.
25. Найти наибольшую величину прогиба рессоры от груза, положенного на ее середину, если статический прогиб ее от того же груза 5 мм.
26.
 |
Під дією сталої сили тіло масою m = 2 кг здійснює прямолінійний рух, що описується рівнянням  . Визначити силу, що діє на тіло через 2 с після початку руху.
. Визначити силу, що діє на тіло через 2 с після початку руху.
27. Невагомий блок закріплено на вершині двох похилих площин, що складають з горизонтом кути відповідно 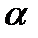 = 30°,
= 30°, 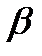 = 45° (рис.). Через блок перекинуто нитку, до кінців якої прикріплено тягарці m 1= 1,5 кг, а m 2= 1 кг. Нехтуючи тертям, знайти силу натягу нитки.
= 45° (рис.). Через блок перекинуто нитку, до кінців якої прикріплено тягарці m 1= 1,5 кг, а m 2= 1 кг. Нехтуючи тертям, знайти силу натягу нитки.
28. Вагон гальмується, і його швидкість за час 0,5 с рівномірно зменшується від 48 до 30 км/год. Яким повинен бути граничний коефіцієнт тертя між чемоданом і полицею, щоб чемодан при гальмуванні не ковзав по ній?
29. На двох паралельних пружинах однакової довжин
 2017-10-25
2017-10-25 1265
1265








