Примеры решения задач. Пример 9.1(2299) Вычислим массу правого лепестка лемнискаты , если линейная плотность в каждой точке кривой

Пример 9.1 (2299) Вычислим массу правого лепестка лемнискаты , если линейная плотность в каждой точке кривой .

Решение. Построим правую часть лемнискаты. Она лежит в секторе . (См. рис.9.2)

Воспользуемся формулами (9.10) и (9.12). Упростим подкоренное выражение.

 

, .

 

Рисунок 9.2

.

И учитывая, что , подставим всё в рабочую формулу: После вычисления интеграла получим искомую массу .

Обратите внимание на то, что несмотря на симметричную форму лепестка лемнискаты, при составлении интеграла нельзя использовать эту симметрию, так как функция плотности не является чётной на интервале .

Пример 9.2. (2307) Найдём координаты центра тяжести полуарки циклоиды

. Линейную плотность кривой будем считать равной единице.

Решение. Построим эскиз к задаче (см. рис. 9.3). Параметр вдоль кривой меняется от до . Воспользуемся формулами (9.9), (9.12), (9.14) при . Вычислим .

Т.к.

Рисунок 9.3

Подставим полученное выражение в формулы.

Массапо формуле (9.12):

По формулам (9.14) вычислим координаты искомой точки.

. Ответ:

 

Пример 9.3. Вычислим момент инерции материальной кривой, которая является пересечением полусферы и плоскости , если плотность . Решение. Построим обе заданные поверхности и линию их пересечения 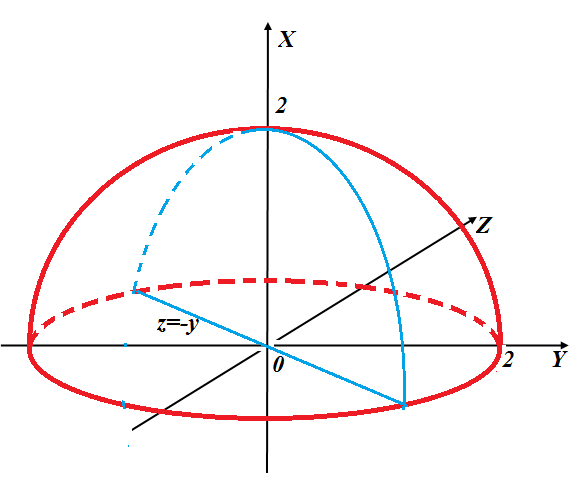(см. рис. 9.4).

Рисунок 9.4

Момент инерции пространственной кривой относительно начала координат вычисляется по следующей формуле: . (см. (9.15))

Кривая задана уравнениями при .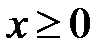

 

Перейдём к её параметрическому заданию. Заметим, что для точек кривой выполняются уравнения . Тогда пусть при . (см. примечание б)) При этом дифференциал дуги кривой , плотность . Подставляем всё в рабочую формулу: . И после вычисления интеграла получаем ответ: .

 

Занятие 10.

Определение криволинейного интеграла второго рода. Теорема существования и свойства. Вычисление криволинейного интеграла второго рода с помощью определенного интеграла для случаев явно заданной функции и параметрически заданной функции. Работа силы при перемещении материальной точки единичной массы из точки А в точку В вдоль кривой АВ. ОЛ-1 гл.5, ОЛ-2 гл.2, ОЛ-4 гл. 3 § 10

Практика: ОЛ-6 №№ Л 6 №№ 2310, 2313, 2314, 2315, 2325 или ОЛ-5 №№ 10.72, 74, 76, 78.

Домашнее задание к занятию 10: ОЛ-6 №№ 2312, 2316, 2322, 2324 или ОЛ-5 №№ 10.71, 73, 77, 81.