2017-11-01
15436
Криволинейный интеграл 2-ого рода вычисляется так же, как криволинейный интеграл 1-ого рода сведением к определённому. Для этого все переменные под знаком интеграла выражают через одну переменную, используя уравнение той линии, вдоль которой производится интегрирование.
а) Если линия АВ задана системой уравнений 
то
(10.3)
Для плоского случая, когда кривая задана уравнением 
криволинейный интеграл вычисляется по формуле: 
. (10.4)
Если линия АВ задана параметрическими уравнениями 
то
(10.5)
Для плоского случая, еслилиния АВ задана параметрическими уравнениями 
, криволинейный интеграл вычисляется по формуле:
, (10.6)
где 
- значения параметра t, соответствующие начальной и конечной точкам пути интегрирования.
Если линия АВ кусочно-гладкая, то следует воспользоваться свойством аддитивности криволинейного интеграла, разбив АВ на гладкие дуги.
Пример 10.1 Вычислим криволинейный интеграл 
вдоль контура, состоящего из части кривой 
от точки 
до 
и дуги эллипса 
от точки до 
.
| Рисунок 10.2 |
Решение. Построим заданный контур 
на плоскости в системе 
|
|
|
(см. рис. 10.2)
| Рисунк 10.1 |
. Сведём оба интеграла к определённым. Часть контура 
задана уравнением относительно переменной 
. Воспользуемся формулой (10.4), в которой поменяем ролями переменные. Т.е.
. После вычисления получим 
.
Для вычисления интеграла по контуру ВС перейдём к параметрической форме записи уравнения эллипса и воспользуемся формулой (10.6).
Обратите внимание на пределы интегрирования. Точке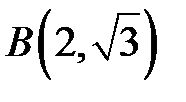 
соответствует значение 
, а точке 
соответствует 
Ответ: 
.
Пример 10.2. Вычислим 
вдоль отрезка прямой АВ, где А(1,2,3), В(2,5,8).
Решение. Задан криволинейный интеграл 2-ого рода. Для вычисления необходимо преобразовать его в определённый. Составим уравнения прямой. Её направляющий вектор имеет координаты 
.
Канонические уравнения прямой АВ: 
.
Параметрические уравнения этой прямой: 
, 
При 
.
Воспользуемся формулой (10.5):
.
Вычислив интеграл, получим ответ: 
.
5. Работа силы при перемещении материальной точки единичной массы из точки 
в точку 
вдоль кривой 
.
Пусть в каждой точке кусочно –гладкой кривой 
задан вектор, имеющий непрерывные функции-координаты: 
. Разобьём эту кривую на 
малых частей точками 
так, чтобы в точках каждой части 
значение функций 
можно было считать постоянными, а сама часть 
могла быть принята за отрезок прямой (см. рис. 10.1). Тогда 
. Скалярное произведение постоянной силы, роль которой играет вектор 
, на прямолинейный вектор перемещения 
численно равно работе, которую совершает сила при перемещении материальной точки вдоль . Составим интегральную сумму 
. В пределе при неограниченном увеличении числа разбиений получим криволинейный интеграл 2-ого рода
|
|
|
. (10.7) Таким образом, физический смысл криволинейного интеграла 2-ого рода 
- это работа, произведённая силой 
при перемещении материальной точки от А к В по контуру L.
Пример 10.3. Вычислим работу, производимую вектором 
при перемещении точки вдоль части кривой Вивиани, заданной как пересечение полусферы 
и цилиндра 
, пробегаемой против часовой стрелки, если смотреть с положительной части оси OX.
Решение. Построим заданную кривую как линию пересечения двух поверхностей (см. рис. 10.3).
| Рисунок 10.3 |
. Воспользуемся формулой (10.7):
| Рисунок 10.3 |
.
Чтобы свести подынтегральное выражение к одной переменной, перейдём в цилиндрическую систему координат: 
.
Т.к. точка перемещается по кривой 
, то удобно в качестве параметра выбрать переменную 
, которая вдоль контура меняется так, что 
. Тогда получаем следующие параметрические уравнения этой кривой:
.При этом 
.
Подставим полученные выражения в формулу для вычисления циркуляции:
(
- знак + указывает на то, что движение точки по контуру происходит против часовой стрелки)
Вычислим интеграл и получим ответ: 
.
Занятие 11.
Формула Грина для односвязной области. Независимость криволинейного интеграла от пути интегрирования. Формула Ньютона-Лейбница. Нахождение функции по ее полному дифференциалу с помощью криволинейного интеграла (плоский и пространственный случаи).
ОЛ-1 гл.5, ОЛ-2 гл.3, ОЛ-4 гл.3 § 10, п. 10.3, 10.4.
Практика: ОЛ-6№№ 2318(а,б,д),2319(а,в),2322(а,г),2327,2329 илиОЛ-5 №№10.79, 82, 133, 135, 139.
Домашнее здание к занятию 11: ОЛ-6 №№ 2318 (в,г), 2319(в,г), 2322(б,в), 2328, 2330 или ОЛ-5 №№ 10.80, 134, 136, 140
Формула Грина.
Пусть на плоскости 
дана односвязная область 
, ограниченная кусочно- гладким замкнутым контуром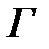 
. (Область называется односвязной, если в ней любой замкнутый контур может быть стянут в точку этой области).
Теорема. Если функции 
и их частные производные 
непрерывны в замкнутой области 
Г, то
| Рисунок 11.1 |
- формула Грина. (11.1)
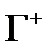обозначает положительное направление обхода (против часовой стрелки).
Пример 11.1. Используя формулу Грина, вычислим интеграл 
по контуру, состоящему из отрезков OA, OB и большей дуги окружности 
, соединяющей точки A и B, если 
, 
, 
.
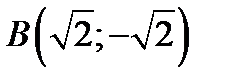Решение. Построим контур 
(см. рис.11.2). Вычислим необходимые производные.
| Рисунок 11.2 |
, 
; 
, 
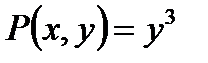. Функции и их производные непрерывны в замкнутой области, ограниченной данным контуром. По формуле Грина данный интеграл 
.
После подстановки вычисленных производных получаем
. Двойной интеграл вычислим, переходя к полярным координатам: 
.
Проверим ответ, вычислив интеграл непосредственно по контуру как криволинейный интеграл 2-ого рода. 
.
.
.
Ответ: 
.
2. Независимость криволинейного интеграла от пути интегрирования.
Пусть 
и 
- произвольные точки односвязной области 
пл. 
. Криволинейные интегралы, вычисленные по различным кривым, соединяющим эти точки, в общем случае имеют различные значения. Но при выполнении некоторых условий все эти значения могут оказаться одинаковыми. Тогда интеграл не зависит от формы пути, а зависит только от начальной и конечной точек.
Имеют место следующие теоремы.
Теорема 1. Для того, чтобы интеграл 
не зависел от формы пути, соединяющего точки 
и 
, необходимо и достаточно, чтобы этот интеграл по любому замкнутому контуру был равен нулю.
Теорема 2.. Для того, чтобы интеграл 
по любому замкнутому контуру был равен нулю, необходимо и достаточно, чтобы функции и их частные производные были непрерывны в замкнутой области Г и чтобы выполнялось условие 
(11.2)
|
|
|
Таким образом, если выполняются условия независимости интеграла от формы пути (11.2), то достаточно указать только начальную и конечную точки: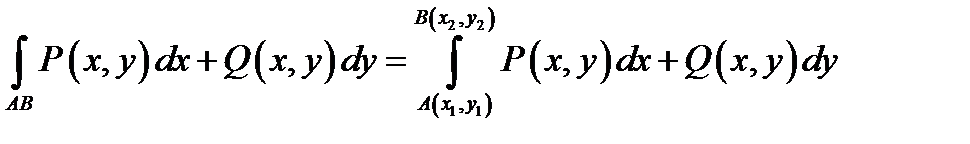 
(11.3)
Теорема 3. Если в односвязной области 
выполняется условие , то существует функция 
такая, что 
. (11.4)
Эта формула называется формулой Ньютона – Лейбница для криволинейного интеграла.
Замечание. Напомним, что равенство является необходимым и достаточным условием того, что выражение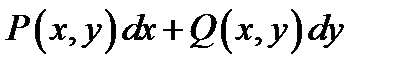 
является полным дифференциалом некоторой функции .
Тогда из выше сформулированных теорем следует, что если функции и их частные производные 
непрерывны в замкнутой области Г, в которой даны точки 
и 
, и , то
а) существует функция , такая, что 
,
б) криволинейный интеграл от полного дифференциала некоторой функции не зависит от формы пути, 
,
в) имеет место формула Ньютона – Лейбница 
.
Пример 11.2. Убедимся в том, что интеграл 
не зависит от формы пути, и вычислим его.
Решение. 
.
| Рисунок 11.3 |
Проверим выполнение условия (11.2). 
. Как видим, условие выполнено. Значение интеграла не зависит от пути интегрирования. Выберем путь интегрирования. Наиболее
простым путём для вычислений является ломаная линия АСВ, соединяющая точки начала и конца пути. (См. рис. 11.3)
Тогда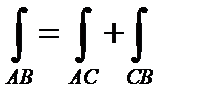 
.
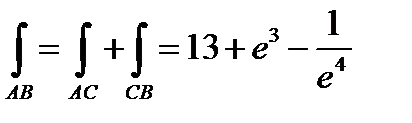
3. Нахождение функции по её полному дифференциалу.
С помощью криволинейного интеграла, который не зависит от формы пути, можно найти функцию , зная её полный дифференциал. Эта задача решается следующим образом.
Если функции и их частные производные непрерывны в замкнутой области Г и 
, то выражение 
является полным дифференциалом некоторой функции . Кроме этого интеграл 
, во-первых, не зависит от формы пути и, во-вторых, может быть вычислен по формуле Ньютона – Лейбница.
Вычислим двумя способами.
| Рисунок 11.4 |
точку с конкретными координатами и точку 
с произвольными координатами. Вычислим криволинейный интеграл по ломаной, состоящей из двух отрезков прямых, соединяющих эти точки, причём один из отрезков параллелен оси 
, а другой – оси 
. Тогда 
. (См. рис. 11.4)|
|
|
Уравнение 
.
Уравнение 
.
Получаем: 
Вычислив оба интеграла, получаем в ответе некоторую функцию 
.
б) Теперь тот же интеграл вычислим по формуле Ньютона – Лейбница.
.
Теперь сравним два результата вычисления одного и того же интеграла. Функциональная часть ответа в пункте а) является искомой функцией , а числовая часть – её значением в точке 
.
Пример 11.3. Убедимся в том, что выражение 
является полным дифференциалом некоторой функции и найдём её. Проверим результаты вычисления примера 11.2 по формуле Ньютона-Лейбница.
Решение. Условие существования функции (11.2) было проверено в предыдущем примере. Найдём эту функцию, для чего воспользуемся рисунком 11.4, причём примем за 
точку 
. Составим и вычислим интеграл по ломаной АСВ, где 
:
.
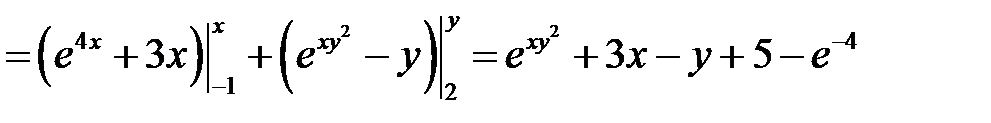Как было сказано выше, функциональная часть полученного выражения и есть искомая функция 
.
Проверим результат вычислений из примера 11.2 по формуле Ньютона –Лейбница:
.
Результаты совпали.
Замечание. Все рассмотренные утверждения верны и для пространственного случая, но с большим количеством условий.
Пусть кусочно-гладкая кривая 
принадлежит области 
в пространстве 
. Тогда, если функции 
и их частные производные непрерывны в замкнутой области 
, в которой даны точки 
и 
, и 
(11.5), то
а) выражение 
является полным дифференциалом некоторой функции 
,
б) криволинейный интеграл от полного дифференциала некоторой функции не зависит от формы пути и 
,
в) имеет место формула Ньютона – Лейбница 
.(11.6)
Пример 11.4. Убедимся в том, что выражение 
является полным дифференциалом некоторой функции и найдём её.
Решение. Для ответа на вопрос о том, является ли данное выражение полным дифференциалом некоторой функции , вычислим частные производные от функций 
, 
, 
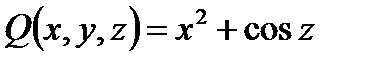. (См. (11.5)) 
; 
; 
; 
; 
; 
.
Эти функции непрерывны вместе со своими частными производными в любой точке пространства 
.
Видим, что выполняются необходимые и достаточные условия существования : 
, 
, 
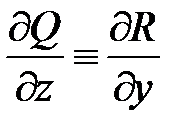, ч. т. д.
Т.е. 
.
Для вычисления функции воспользуемся тем, что линейный интеграл не зависит от пути интегрирования и может быть вычислен по формуле Ньютона-Лейбница. Пусть точка 
- начало пути, а некоторая точка 
- конец пути. Вычислим интеграл
по контуру, состоящему из отрезков прямых, параллельных координатным осям. (см.рис.11.5).
.
| Рисунок 11.5 |
, 
, 
.
Тогда 
, x здесь зафиксирован, поэтому 
,
, здесь зафиксирован y, поэтому 
.
В итоге получаем: 
.
Теперь тот же интеграл вычислим по формуле Ньютона-Лейбница.
Приравняем результаты: 
.
Из полученного равенства следует, что 
, а 
Ответ: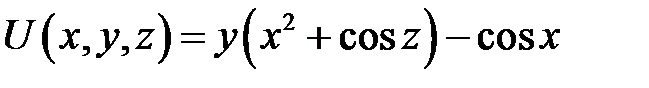 
.
Занятие 12.
Поверхностный интеграл первого рода: определение, основные свойства. Правила вычисления поверхностного интеграла первого рода с помощью двойного интеграла. Приложения поверхностного интеграла первого рода: площадь поверхности, масса материальной поверхности, статические моменты относительно координатных плоскостей, моменты инерции и координаты центра тяжести. ОЛ-1 гл.6, ОЛ 2 гл.3, ОЛ-4§ 11.
Практика: ОЛ-6 №№ 2347, 2352, 2353 или ОЛ-5 №№ 10.62, 65, 67.
Домашнее задание к занятию 12:
ОЛ-6 №№ 2348, 2354 или ОЛ-5 №№ 10.63, 64, 68.
