1.Если кривая задана в пространстве как пересечение двух поверхностей 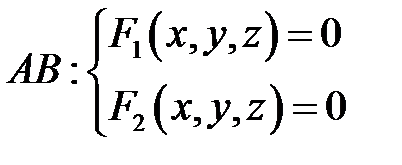 , то можно выразить из системы уравнений этих поверхностей две переменные через третью, например,
, то можно выразить из системы уравнений этих поверхностей две переменные через третью, например, 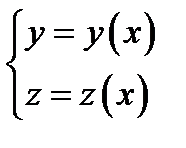 . Тогда длина отрезка прямой
. Тогда длина отрезка прямой 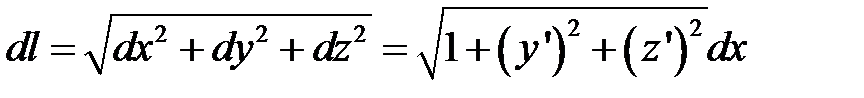 и
и
 . (9.8)
. (9.8)
2.Если кривая задана параметрически уравнениями: 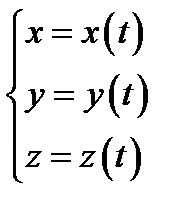 , то длина отрезка прямой
, то длина отрезка прямой 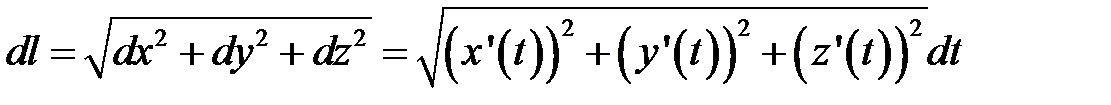 , и
, и
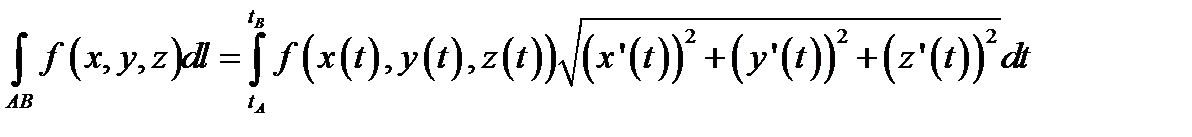 (9.9)
(9.9)
3.Если задана плоская кривая и в каждой её точке определена функция 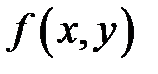 , то формулы (9.8) и (9.9) упрощаются:
, то формулы (9.8) и (9.9) упрощаются: 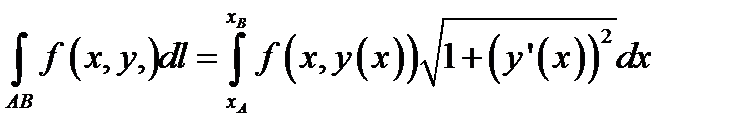 , (9.8а)
, (9.8а) 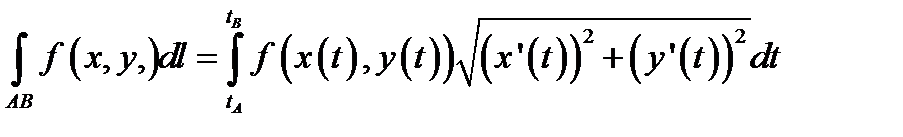 . (9.9а)
. (9.9а)
4.Если на плоскости кривая задана в полярной системе уравнением 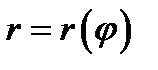 , то
, то
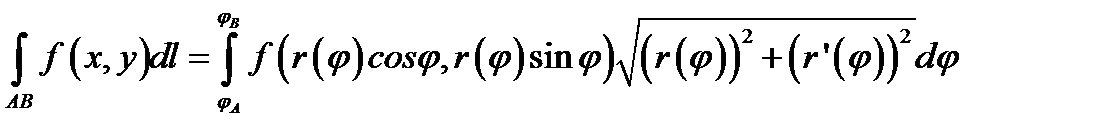 (9.10)
(9.10)
Примечание. а) Если контур интегрирования – отрезок прямой, соединяющий точки 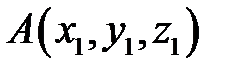 и
и 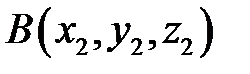 , то уравнения этого контура имеют вид
, то уравнения этого контура имеют вид 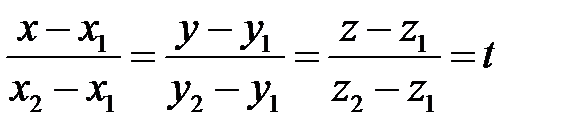 . б) Если контуром интегрирования является эллипс
. б) Если контуром интегрирования является эллипс 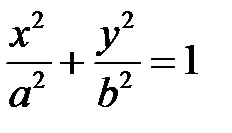 , то удобно перейти к параметрическому заданию этой кривой, где
, то удобно перейти к параметрическому заданию этой кривой, где 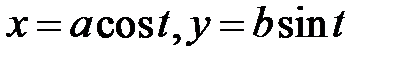 (частный случай – окружность с
(частный случай – окружность с 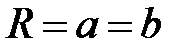 ).
). 
Теорема существования криволинейного интеграла 1 рода.
Если 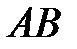 – кусочно-гладкая кривая и функция
– кусочно-гладкая кривая и функция 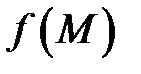 непрерывна на ней, то существует криволинейный интеграл I-го рода от этой функции (функция интегрируема по кривой
непрерывна на ней, то существует криволинейный интеграл I-го рода от этой функции (функция интегрируема по кривой 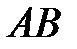 ), то есть существует предел
), то есть существует предел 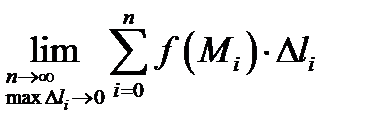 и он не зависит от способа разбиения кривой на части и от выбора промежуточных точек.
и он не зависит от способа разбиения кривой на части и от выбора промежуточных точек.
5.Физические приложения криволинейного интеграла первого рода.
А) Масса материальной кривой.
Если 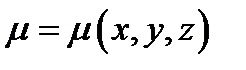 - линейная плотность кривой, то масса этой кривой
- линейная плотность кривой, то масса этой кривой 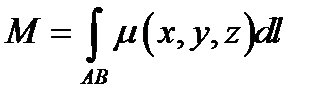 (9.12)
(9.12)
б) Статистические моменты плоской кривой относительно осей 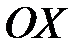 и
и 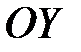 .
.
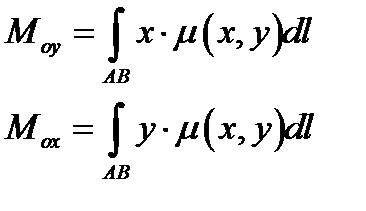 (9.13)
(9.13)
 2017-11-01
2017-11-01 2009
2009








