2017-11-01
1014
Если функция 
непрерывна в каждой точке кусочно - гладкой кривой, то она интегрируема по этой кривой по переменной 
, т.е. существует предел последовательности интегральных сумм 
и он не зависит от способа разбиения кривой на части и выбора промежуточных точек. 
. (10.2) 3. Основные свойства криволинейного интеграла 2-ого рода.
1. Линейность. Криволинейный интеграл 2-ого рода от линейной комбинации интегрируемых по кривой функций равен линейной комбинации интегралов от этих функций. В частности,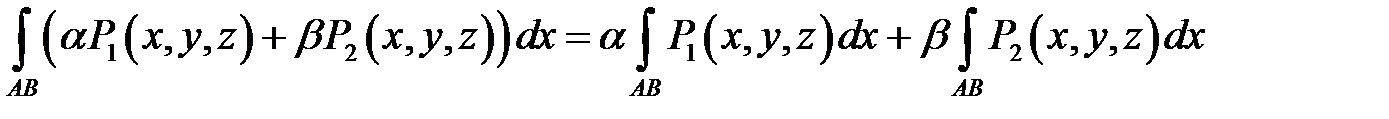 
. 2. Аддитивность. Если кривая 
разбита на две части, не имеющие общих внутренних точек, то 
.
3. Изменение знака при изменении направления движения по кривой. 
. Это свойство отличается от аналогичного свойства для ранее рассмотренных интегралов. Появление минуса связано с тем, что в соответствующей интегральной сумме при изменении направления перемещения точки по кривой изменит свой знак 
. А следовательно, изменит знак и интеграл (см. (10.2)).
