2017-10-25
724
Розглянемо другу задачу теорії кореляції.
Величиною, що виражає прямолінійну залежність між ознаками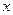 
та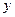 
, є коефіцієнт кореляції, який обчислюється за формулою
.
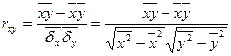Властивості коефіцієнта кореляції:
1. 
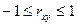, тобто 
. Якщо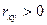 
, то кореляція додатня (при зростанні значення ознаки 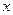значення ознаки 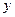теж зростають); якщо 
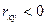, то кореляція від’ємна (із зростанням значення ознаки 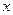значення ознаки 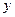спадають).
2. Якщо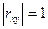 
, то ознаки 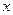та 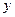пов’язані функціональною залежністю (лінійною).
3. Якщо 
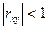, то між ознаками 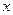та 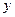існує кореляційна залежність, при чому цей зв’язок тим тісніший, чим ближче 
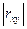до 1.
4. Якщо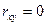 
, то ознаки 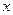та 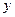- незалежні, тобто не зв’язані кореляційною залежністю.
ЗАВДАННЯ. На основі вибірки обсягу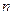 
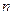( - задається), здійсненої з таблиці генеральної сукупності(зріст і вага учнів випускних класів), визначити і знайти форму зв’язку між заданими ознаками. Обчислити коефіцієнт кореляції, за допомогою якого зробити висновки про силу кореляційного зв’язку між ознаками.
СТАТИСТИЧНА ПЕРЕВІРКА ГІПОТЕЗ
Мета: Ознайомити з статистичними гіпотезами та їх різновидами, з похибками перевірки гіпотез, з критеріями узгодження для перевірки гіпотез. Навчити застосовувати критерій Пірсона для перевірки гіпотези про нормальний закон розподілу генеральної сукупності.
