Хід виконання завдання

1. Записати інтервальний статистичний ряд розподілу абсолютних частот або просто частот (див. завд.2, п.4 лаб. роботи №1)

2. Перейти від інтервальної таблиці таблиці частот до дискретної таблиці частот з рівновіддаленими варіантами, кожна з яких є серединою частинного інтервалу:

3. Обчислити вибіркову середню і вибіркове середнє квадратичне відхилення .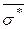

4. Скласти розрахункову таблицю 1, зразок якої наводиться у звіті до цієї лабораторної роботи.

5. Скласти розрахункову таблицю 2, в якій записуються емпіричні та теоретичні частоти і обчислюється 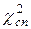(зразок табл. наводиться у звіті до цієї лабораторної роботи).

6. Знайти число ступенів вільності критерія за формулою , де к – число інтервалів вибірки.

7. Знайти за таблицею значень критерію Пірсона (див. додаток до цієї лабораторної роботи) критичну точку 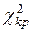, яка відповідає заданому рівню значущості та ступеню вільності .

8. Порівняти 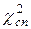і 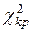і зробити висновок:

а) якщо , то гіпотезу треба прийняти.

б) якщо , то гіпотезу треба відхилити

Таким чином, дані вибірки узгоджуються (не узгоджуються) з гіпотезою про нормальний розподіл генеральної сукупності тому, що розбіжності емпіричних та теоретичних частот незначні (значні).