В пункті а) кожного завдання зробити всі необхідні пояснення і провести обчислення, використавши програму Калькулятор. В пункті б) провести необхідні обчислення, використавши стандартні функції середовища Excel. Пункт в) – в середовищі Excel перевірити правильність обчислень пункту а).
Приклад.
У ящику є 4 деталі першого виду, 5 деталей другого виду та 3 деталі третього виду. Навмання вибирають 2 деталі. Знайти ймовірність того, що це деталі одного виду.
Зразок виконання завдання.
а) 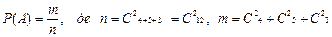
Тоді 
б)
| k | |
| l | |
| s | |
| r | |
| m | |
| n | |
| P(a) | 0,287879 |
Для знаходження комбінацій використовується функція ЧИСЛКОМБ.
Контрольні запитання
1. Як ви розумієте поняття сполуки?
2. Що нас цікавить у кожному з видів сполук?
3. Що таке комбінаторика?
4. Дайте означення розміщення з n елементів по m елементів. Яке співвідношення існує між натуральними числами n та m? Як символічно записується число розміщень з n по m?
5. За якою формулою обчислюється Amn?
6. Дайте означення перестановки з n елементів.
7. Сформулюйте означення комбінації з n елементів по m елементів.
8. За якими формулами обчислюється кількість комбінацій з n елементів по m елементів?
9. Чим відрізняються між собою розміщення і комбінації з n елементів по m елементів?
10. Чого більше – розміщень чи комбінацій з n елементів по m елементів?
11. Сформулюйте комбінаторні правила суми та добутку.
Лабораторна робота №3
ТЕМА: ЙМОВІРНІСТЬ СКЛАДЕНОЇ ПОДІЇ.
Мета: Навчитись користуватися алгоритмами для знаходження ймовірності складеної події, в описі якої є сполучники «або» та «і», знаходження ймовірності появи хоча б однієї з незалежних подій. Навчитися використовувати формули повної ймовірності та Байєса.
Обладнання: Комп’ютер, таблиці «Аналогія між множинами та подіями» та «Основні теореми теорії ймовірностей та наслідки з них».
Теоретичні відомості
Основні поняття теорії множин та означення операцій над множинами з відповідною їх геометричною інтерпретацією подано в таблиці 1.
Таблиця 1. Аналогія між множинами та подіями
| ТЕОРІЯ МНОЖИН | ГЕОМЕТРИЧНА ІНТЕРПРЕТАЦІЯ (діаграми Ейлера — Венна) | ТЕОРІЯ ЙМОВІРНОСТЕЙ | |||||
| U — універсальна множина |  | Ω — простір елементарних подій | |||||
| Елемент a множини U | 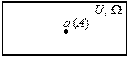 | Елементарна подія A з Ω | |||||
| А — підмножина U | 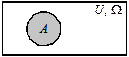 | А — випадкова подія з Ω | |||||
| Порожня множина — Ø | Æ = V | V — неможлива подія з Ω | |||||
| Універсальна множина U | Ω = U | U — вірогідна подія з Ω | |||||
| А — підмножина В | 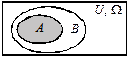 A Ì B A Ì B | Поява події А спричиняє появу події В | |||||
| Об’єднанням (сумою) множин А та В називають множину С, яка складається з тих елементів, що належать принаймні до однієї з множин А або В | 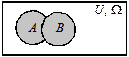 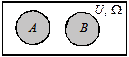 C = A È B (C = A + B) C = A È B (C = A + B) | Об’єднанням (сумою) подій А та В називають подію С, яка відбувається тоді, коли відбувається принаймні одна з подій А або В | |||||
| Перерізом (добутком) множин А та В називають множину С, яка складається з тих елементів, які належать і множині А, і множині В |  C = A Ç B (C = AB) C = A Ç B (C = AB) | Перерізом (добутком) подій А та В називають подію С, яка відбувається тоді, коли відбуваються одночасно обидві події А і В | |||||
| Різницею двох множин А та В називають множину С, яка складається з тих елементів множини А, які не належать множині В | 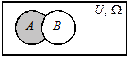 C = A \ B (C = A – B) C = A \ B (C = A – B) | Різницею подій А та В називають подію С, яка відбувається тоді, коли подія А відбувається, а подія В не відбувається | |||||
| Доповненням множини А відносно множини U називають множину, яка складається з усіх тих елементів множини U, які не належать множині А, позначається С UА | 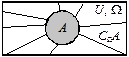 СΩ А = Ω – А ( СΩ А = Ω – А (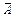 = U – A) = U – A) | Протилежною подією до події А є подія 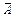 , яка відбувається тоді, коли подія А не відбувається , яка відбувається тоді, коли подія А не відбувається | |||||
| Якщо A Ç B = Æ, то А та В — множини, які не перетинаються | 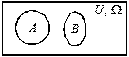 | Якщо АВ = V, то А та В — несумісні події, тобто поява однієї події відразу виключає появу іншої | |||||
| Дві множини А та В називають рівними, якщо вони складаються з одних і тих же елементів |  A Ì B і B Ì A (A = B) A Ì B і B Ì A (A = B) | Дві події А та В називають рівними, якщо вони одночасно або відбуваються, або не відбуваються | |||||
| Властивості операцій над множинами (подіями) | |||||||
| 1. | А + В = В + А | 8. | АА = А | 15. | 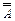 = A = A | ||
| 2. | АВ = ВА | 9. | АU = A | 16. |  = V = V | ||
| 3. | (А + В) + С = А + (В + С) | 10. | A + U = U | 17. | 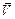 = U = U | ||
| 4. | (АВ) С = А (ВС) | 11. | A + V = A | 18. | 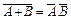 | ||
| 5. | (А + В) С = АС + ВС | 12. | AV = V | 19. | 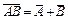 | ||
| 6. | АВ + С = (А + С)(В + С) | 13. | A + 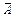 = U = U | ||||
| 7. | А + А = А | 14. |  | ||||
Під час виконання операцій множення подій важливо встановити незалежність або залежність між ними. Поняття незалежності подій є дуже важливим у теорії ймовірностей.
Дві події називають незалежними, якщо ймовірність появи однієї з них не залежить від того, відбулася інша подія чи ні. В іншому випадку події будуть залежними.
Взагалі, якщо дано кілька подій, кожні дві з яких є незалежними, то ці події вважають попарно незалежними.
Кілька подій називають незалежними в сукупності (або просто незалежними), якщо незалежні кожні дві з них, незалежна кожна подія і всі можливі добутки решти.
Теореми, які дають можливість за заданими ймовірностями простих подій обчислювати ймовірності складених подій, якщо останні можна подати у вигляді суми чи добутку таких подій, наводяться у таблиці 2.
Таблиця 2. Основні теореми теорії ймовірностей та наслідки з них
| Теорема 1. Імовірність суми двох несумісних подій А і В дорівнює сумі ймовірностей цих подій, тобто | |
| Р (А + В) = Р (А) + Р (В). | (1) |
Наслідок 1. Сума ймовірностей протилежних подій дорівнює одиниці, тобто Р (А) + Р (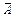 ) = 1. ) = 1. | (2) |
| Наслідок 2. Якщо події А 1, А 2,..., Аn — попарно несумісні, то | |
| Р (А 1 + А 2 + … + Аn) = Р (А 1) + Р (А 2) + … + Р (Аn). | (3) |
| Наслідок 3.Якщо попарно несумісні події А 1, А 2 ,..., Аn утворюють повну групу, то Р(А 1 ) + Р(А 2 ) + … + Р(Аn) = 1. | (4) |
| Теорема 2. Імовірність добутку двох незалежних подій А і В дорівнює добутку ймовірностей цих подій, тобто Р (АВ) = Р (А) Р (В). | (5) |
| Наслідок 1. Якщо події А 1, А 2,..., А n є незалежними у сукупності, то ймовірність добутку цих подій дорівнює добутку їх ймовірностей, тобто Р (А 1× А 2×…× A n) = Р (А 1) Р (A 2)… P (A n). | (6) |
| Теорема 3. Якщо події А 1, А 2, …, A n — незалежні у сукупності, то ймовірність здійснення принаймні однієї з них може бути виражена через імовірності цих подій за формулою | |
| Р (А) = 1 – (1 – Р (А 1))(1 – Р (А 2))…(1 – Р (Аn)). | (7) |
| Наслідок 1. Якщо Р (А 1) = Р (A 2) = … = P (An) = p, то Р (А) = 1 – (1 – p) n. | (8) |
| Теорема 4. Ймовірність добутку двох залежних подій А і В дорівнює добутку ймовірності однієї з них на умовну ймовірність другої події, за умови, що перша подія відбулася Р (А×В) = Р (А) Р (В/А)або Р(А×В) = Р(В)Р(А/В) | (9) |
| Наслідок 1.Якщо події А 1, А 2,..., А n є залежними, то ймовірність добутку цих подій дорівнює добутку ймовірностей однієї з них на умовні ймовірності всіх інших подій, причому ймовірність кожної наступної події обчислюється у припущенні, що всі попередні події уже відбулися Р (А 1× А 2×…× A n) = Р (А 1) Р (А 2 /А 1) Р (А 3 /А 1 А 2)×…× Р (А n /А 1 А 2×…× A n-1) | (10) |
| Теорема 5.Ймовірність події А, яка може настати лише за умови появи однієї з попарно несумісних подій (гіпотез) Н 1, Н 2,..., Н n , які утворюють повну групу подій, дорівнює сумі добутків ймовірностей кожної з цих подій на відповідну умовну ймовірність події А Р (А) = Р (Н 1) Р (А/Н 1) + Р (Н 2) Р (А/Н 2) +…+ Р (Н n) Р (А/Н n) (формула повної ймовірності) | (11) |
Для того, щоб переоцінити ймовірності гіпотез після того, як стане відомим результат випробування, внаслідок якого появилась подія А, використовують формули Байєса
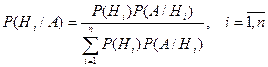
Завдання 1.
1. Ймовірності того, що потрібний робітнику елемент приладу міститься у першому, другому, третьому ящику дорівнює 0,5; 0,7; 0,9. Знайти ймовірність того, що потрібний елемент міститься:
а) не менше, ніж у двох ящиках; б) у двох ящиках; в) хоча б у одному ящику.
2. Ймовірність вчасного повернення кредиту для першої фірми становить 0,7, для другої – 0,8, для третьої – 0,9. Знайти ймовірності того, що вчасно повернуть кредит:
а) всі фірми; б) лише одна фірма; в) хоча б одна фірма.
3. Троє мисливців зробили по одному пострілу в мішень. Ймовірність непопадання для них відповідно рівні 0,6; 0,7; 0,8. Знайти ймовірності того, що:
а) жоден не влучив; б) хоча б один влучив; в) влучило менше двох мисливців.
4. Три студенти, незалежно один від одного вимірюють деяку фізичну величину. Ймовірність того, що перший допустить помилку під час зчитування показів приладу рівна 0,1, для другого ця ймовірність – 0,15, для третього – 0,2. Знайти ймовірність того, що під час вимірювання не допустить помилку:
а) хоча б один зі студентів; б) всі студенти; в) не менше 2-х студентів.
5. Для сигналізації про аварію встановлено три сигналізатори, які працюють незалежно один від одного. Ймовірність того, що під час аварії спрацює спрацює перший сигналізатор дорівнює 0,75, для другого і третього ймовірності відповідно дорівнюють 0,8 і 0.85. Знайти ймовірність того, що при аварії не спрацює:
а) тільки один сигналізатор; б) хоча б один сигналізатор; в) менше двох сигналізаторів.
6. В радіоприймачі знаходяться радіолампи трьох видів. Ймовірність виходу з ладу протягом часу Т для кожної лампи першого виду дорівнює 0,1, для другого і третього видів – 0,2 і 0,25. Знайти ймовірність виходу радіоприймача з ладу в результаті виходу із ладу:
а) хоча б однієї лампи; б) не менше двох ламп; в) трьох ламп.
7. Працівник обслуговує три станки, що працюють незалежно один від одного. Ймовірність того, що на протязі години перший станок вимагатиме уваги працівника, дорівнює 0,15, а для другого і третього станка – 0,2 і 0,15 відповідно. Знайти ймовірність того, що протягом години не вимагатимуть уваги працівника:
а) три станки; б) хоча б два станки; в) менше двох станків.
8. Ймовірності того, що потрібна студентові сума грошей є в одного з його трьох друзів відповідно дорівнюють 0,65; 0,75; 0,85. Знайти ймовірність того, що необхідна сума грошей є:
а) не менше ніж у одного з друзів; б) в усіх друзів; в) хоча би у двох друзів.
9. Ймовірність прибуткової діяльності для першої фірми складає 0,7, для другої – 0,5, для третьої ця ймовірність у три рази менша від суми ймовірностей перших двох фірм. Знайти ймовірність того, що прибутковими будуть:
а) дві фірми; б) хоч би дві фірми; в) менше двох фірм.
10. Ймовірність невиконання договору для першого підприємства становить 3/5, для другого і третього підприємств ці ймовірності відповідно дорівнюють 1/2 і 1/5. Знайти ймовірність виконання договору:
а) хоча б одним підприємством; б) трьома підприємствами; в) менше, ніж двома підприємствами.
11. Ймовірність банкрутства для першої фабрики складає 0,2, для другої – на 50% більше ніж для першої, для третьої ця ймовірність дорівнює 0,1. Знайти ймовірність банкрутства:
а) тільки однієї фабрики; б) хоча б двох фабрик; в) не більше однієї фабрики.
12. Ймовірність того, що справним є перший комп’ютер, складає 4/5, другого – 3/4, третього - 17/20. Знайти ймовірність того, що справними є:
а) хоча б два комп’ютери; б) два комп’ютери; в) менше, ніж два комп’ютери.
13. Ймовірність виготовлення бракованої деталі на першому верстаті складає 0,2, для другого і третього верстатів ці ймовірності відповідно дорівнюють 0,4 і 0,25. На кожному верстаті виготовлено по одній деталі. Знайти ймовірність того, що серед цих деталей буде:
а) не більше двох бракованих; б) дві браковані; в) менше двох бракованих.
14. Ймовірність повного розрахунку за енергоносії для кожного з трьох заводів відповідно дорівнює 0,18; 0,2 і 0,32. Знайти ймовірність вчасної сплати за енергоносії:
а) одним заводом; б) хоча б одним заводом; в) не більше, ніж одним заводом.
15. Ймовірності ліквідації заборгованості для кожного з трьох заводів відповідно дорівнюють 4/5, 3/4, 9/10. Знайти ймовірність ліквідації заборгованості:
а) хоча б двома заводами; б) двома заводами; в) не менше, ніж одним заводом.
ЗАВДАННЯ 2.
1. У ящику знаходиться 20 куль, серед яких 10 білих і 10 червоних. Загублено одну кулю невідомого кольору, а потім навмання витягують одну кулю. Знайти ймовірність того, що витягнута куля є білого кольору.
2. Три верстати-автомати виробляють однакові деталі. Перший виготовляє 25%, другий – 35%, третій – 40% усієї продукції. У їхній продукції брак становить відповідно 5%, 4%, 2%. Яка ймовірність того, що випадково вибрана деталь є бракованою?
3. Для участі у спортивних змаганнях з першого курсу виділили 4 студенти, з другого – 6, з третього – 5 студентів. Ймовірність того, що студент першого, другого, третього курсу потрапить до збірної факультету відповідно дорівнює 0,9; 0,7; 0,3. Випадково вибраний студент потрапив до збірної. Яка ймовірність того, що він з другого курсу?
4. Два цехи штампують однотипні деталі. Перший цех має 10% браку, другий – 15%. Для контролю відібрали 20 деталей першого цеху, 30 деталей другого та з’єднали їх в один комплект. Для контролю вибрали одну деталь і вона виявилась бракованою. Яка ймовірність того, що вона вироблена другим цехом?
5. У продаж надійшли телевізори трьох заводів. Продукція першого заводу містить 20% телевізорів із скритим дефектом, другого – 10%, третього – 5%. У магазин надійшло 30% телевізорів з першого заводу, 20% - з другого, 50% - з третього заводу. Яка ймовірність того, щоб купити телевізор без дефекту?
6. На стандартність виріб перевіряє один з двох контролерів. Ймовірність того, що виріб потрапить до першого контролера 0,6, а до другого – 0,4. Ймовірність того, що якісний виріб буде визнаний якісним першим контролером дорівнює 0,95, другим – 0,9. Яка ймовірність того, що у процесі перевірки якісний виріб буде визнаний якісним?
7. Прилад складається із двох послідовно ввімкнутих вузлів. Надійність першого вузла 0,9, другого – 0,8. У процесі випробування прилад зіпсувався. Яка ймовірність, що зіпсований перший вузол?
8. У пункті прокату є 10 телевізорів, для яких ймовірність того, що протягом місяця телевізор не вийде з ладу дорівнює 0,9 і 5 телевізорів з аналогічною ймовірністю 0,95. Яка ймовірність того, що взятий у пункті прокату телевізор не вийшов з ладу протягом місяця.
9. Є три партії деталей по 30 деталей у кожній. Кількість стандартних деталей у першій, другій і третій партіях відповідно дорівнює 25, 20, 15. З партії випадково взяли деталь, яка виявилась стандартною. Яка ймовірність того, що її взяли з другої партії?
10. Два спортсмени незалежно один від одного стріляють у мішень. Ймовірність влучення у мішень для кожного із стрільців відповідно дорівнюють 0,85 та 0,9. Відомо, що у мішень влучив тільки один із них. Знайти ймовірність того, що це був перший стрілець.
11. У цеху 20 станків, серед яких 10 марки А, 6 марки В, 4 марки С. Ймовірність того, що деталь виготовлена на кожному станку буде відмінної якості відповідно дорівнює 0,8; 0,9; 0,7. Вибірково взята деталь виявилась відмінної якості. Яка ймовірність того, що вона виготовлена на станку марки В?
12. З 10 студентів, що прийшли складати екзамен з ТЙМС і взяли білети, Іван і Петро вивчили 20 білетів з 30, Микола – лише 15, інші знали всі 30 білетів. Знання білета гарантує складання екзамену з ймовірністю 0,85, у разі незнання білета можна скласти екзамен з ймовірністю 0,1. Викликаний екзаменатором студент склав іспит. Яка ймовірність того, що це Микола?
13. На складі є три партії деталей. У першій партії 25% бракованих деталей, у другій і третій – усі деталі якісні. З вибраної партії випадково взяли одну деталь. Яка ймовірність того, що вона виявиться бракованою?
14. Відомо, що 5% усіх чоловіків і 75% всіх жінок хворі хворобою А. Вибрана навмання особа виявилась хворою на хворобу А. Яка ймовірність того, що це був чоловік, якщо чоловіків та жінок було порівну?
15. У лабораторії 10 комп’ютерів, виготовлених фірмою А, 8 комп’ютерів фірми в, 7 – фірми С. Ймовірність того, що протягом місяця комп’ютери працюватимуть без ремонту відповідно дорівнює 0.85; 0,9; 0,95. Яка ймовірність того, що протягом місяця якийсь комп’ютер вийде з ладу?
ЗАВДАННЯ 3.
Сформулювати задачу, використовуючи умову завдання 2, щоб вона розв’язувалась за формулою повної ймовірності (формулою Байєса), якщо задача завдання 2 розв’язувалась за формулою Байєса (формулою повної ймовірності).
 2017-10-25
2017-10-25 1943
1943
