2017-10-25
693
| Випробування | Подія |
| Підкидання одного грального кубика, на гранях якого є надписи 1, 2, 3, 4, 5, 6 | а) поява цифри 4 на верхній грані (А 1); б) поява цифри 7 на верхній грані (V 1); в) поява хоч однієї з шести цифр на верхній грані (U 1). |
Контрольні запитання
1. Що вивчає теорія ймовірностей?
2. Що розуміють під випробуванням (дослідом, експериментом)?
3. Що розуміють під подією в теорії ймовірностей?
4. З якими подіями ми сьогодні ознайомились?
5. Приклади яких стохастичних експериментів ви можете навести?
6. Приклади яких випадкових явищ ви можете навести?
7. Наведіть приклади нестохастичних експериментів.
8. Які події називають однорідними? масовими?
9. Дайте означення відносної частоти події.
10. Які досліди називають статистично стійкими?
11. Що називають статистичною ймовірністю здійснення події?
12. Наведіть приклади статистично стійких дослідів.
Лабораторна робота №2
Тема: Обчислення ймовірності події.
Мета: Навчити використовувати формули та правила комбінаторики до обчислення ймовірності події за формулою класичної ймовірності.
|
|
|
Обладнання: Комп’ютер.
Теоретичні відомості
Ймовірністю випадкової події А називають відношення m — кількості подій, які призводять до появи події А, до кількості n усіх рівноможливих попарно несумісних подій, які утворюють повну групу подій під час певного випробування.
Формула класичної ймовірності випадкової події А має вигляд:
. (1)
Властивості ймовірності події. Використовуючи формулу (1), маємо:
1. P (U) = 1, бо для вірогідної події m = n;
2. P (V) = 0, бо для неможливої події m = 0;
3. 0 < P (A) < 1, бо для випадкової події 0 < m < n.
Отже, для будь-якої події А маємо 0 £ P (A) £ 1, бо m £ n, m ³ 0, n > 0.
Скінченні сукупності предметів відрізняються між собою або кількістю, або порядком розташування, або самими предметами, або порядком і складом предметів тощо. Такі сукупності називають сполуками.
Сполуки можна розглядати як множини елементів. Розділ математики, в якому вивчаються сполуки, називають теорією сполук, або комбінаторикою. У комбінаториці розглядають методи розв’язування задач, у яких йдеться про вибір і розташування елементів деякої скінченної множини. Майже завжди в комбінаторних задачах є слова «Скількома способами…?».
Взагалі, якщо дано скінченну множину 
, то розміщенням з n елементів по т елементів називають будь-яку впорядковану підмножину, яка містить т елементів, де m £ n.
Іншими словами, будь-які два розміщення з n елементів по т елементів відрізняються між собою або складом елементів, або їх порядком.
Кількість усіх розміщень з п елементів по т елементів дорівнює добутку т послідовних натуральних чисел, найбільшим з яких є число п, тобто якщо m £ n, маємо:
|
|
|
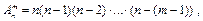(1)
(2)
Будь-яку скінченну множину, яка містить n елементів, можна впорядкувати різними способами. Кожна з упорядкованих множин містить ті ж n елементів, а відрізняються множини між собою лише порядком розташування елементів. Такі впорядковані n -елементні множини називають перестановками з n елементів.
Кількість усіх перестановок з n елементів можна знайти з формули числа розміщень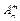 
, якщо m = n:
·...· 
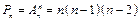або 
·... 
Цю формулу, як правило, записують у зворотному напрямі:
. (3)
Символ n! (ен-факторіал) позначає добуток усіх натуральних чисел від 1 до n.
Використовуючи поняття n!, можна отримати інший вигляд формули для :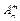
(4)
або 
. (5)
Розглянемо тепер підмножини скінченної множини, які відрізняються одна від одної тільки складом елементів, тобто такі, в яких порядок елементів значення не має. Іншими словами, розглянемо такі підмножини, кожні дві з яких мають принаймні по одному відмінному елементу. Усі такі множини називають комбінаціями.
Комбінацією з n елементів по m елементів називають будь-яку підмножину з m елементів, утворену із множини, яка містить n елементів.
Кількість усіх комбінацій з n елементів по m елементів позначають символом 
, де m £ n.
Число всіх комбінацій з n елементів по m елементів:
. (6)
Використавши формули (1) і (2), отримаємо формулу в іншому вигляді:
. (7)
«Правило суми», можна сформулювати так: Якщо елемент a можна вибрати p різними способами, а після цього елемент b – q різними способами, причому будь-який вибір елемента а не збігається з вибором елемента b, то вибрати елемент а або b можна p + q способами.
«Правило добутку», формулюється так: Якщо елемент a можна вибрати p різними способами і при кожному виборі елемента a елемент b можна вибрати q різними способами, то вибір пари (a, b), тобто a і b, можна здійснити p ∙ q способами.
Все вище сказане можна подати такою таблицею:
| 1. Вибір виду сполуки і відповідної формули | ||
| Чи враховується порядок розміщення елементів? | ||
| Так | Ні | |
| Чи всі елементи входять до сполуки? | ||
| Так | Ні | |
| Перестановки | Розміщення | Комбінації |
 
| 
| 
|
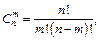| 2. Модель | ||
| Впорядкована множина з n елементів | Впорядкована множина з m різних елементів, кожний з яких вибрано з n -елементної множини. | Довільна множина з m різних елементів, кожний з яких вибрано з n- елементної множини. |
| 3. Характеристичні ознаки | ||
| 1) елементи різні; 2) усі місця зайняті; 3) порядок елементів важливий. | 1) елементи і місця різні; 2) 0 £ m £ n; 3) усі m місць зайняті; 4) порядок елементів важливий. | 1) елементи різні; 2) 0 £ m £ n; 3) порядок вибору елементів не має значення. |
Завдання 1.
1. Із n жетонів, пронумерованих числами від 1 до n, навмання виймають m жетонів. Знайти ймовірність того що номери жетонів виявляться одночасно кратними 4 або 9.
а) n=35, m=2 б) n=200, m=5 в) див. рекомендації до виконання завдань
2.У скриньці лежать m білих, n червоних та k синіх кульок. Навмання вибирають r кульок. Знайти ймовірність того, що вони всі одного кольору.
а) m=7, n=5, k=8, r=3 б) m=45, n=60, k=55, r=20 в) див. рекомендації до виконання завдань
3. На картках написані числа від 1 до n. Навмання вибирають m карток. Знайти ймовірність того, що вибрані числа одночасно будуть або дільниками числа 30, або числами, що діляться на 5.
а) n=30, m=2 б) n=230, m=6 в) див. рекомендації до виконання завдань
4. Знайти ймовірність витягнути з колоди, яка містить n карти, m карт червоної масті.
а) n=36, m=2 б) n=52, m=2 в) див. рекомендації до виконання завдань
5. У шаховому турнірі беруть участь m гросмейстерів, n міжнародних майстрів і r майстрів спорту. Знайти ймовірність того, що за першим столом зустрінуться шахісти одної категорії.
|
|
|
а) m=10, n=6, r=4 б) m=45, n=35, r=20 в) див. рекомендації до виконання завдань
6. У скриньці m ламп потужністю 100 вт і n ламп потужністю 60 вт, які зовні не відрізняються. Знайти ймовірність того, що k випадково вибраних зі скриньки ламп будуть однакової потужності.
а) m=10, n=5, k=2 б) m=100, n=80, k=50 в) див. рекомендації до виконання завдань
7. З колоди на n карт навмання виймають m карт. Знайти ймовірність того, що це карти однієї масті.
а) n=36, m=2 б) n=52, m=4 в) див. рекомендації до виконання завдань
8. Робітник за зміну з m деталей виготовив n деталей вищого ґатунку, k деталей – другого ґатунку, решта – першого. Знайти ймовірність того, що з навмання вибраних r деталей всі будуть одного ґатунку.
а) m=50, n=20, k=20, r=2 б) m=250, n=60, k=100, r=15 в) див. рекомендації до виконання завдань
9. В лотереї є m білетів, серед яких n виграшів по 50 грн., k виграшів по 20 грн., r виграшів по 10 грн. і p виграшів по 2 грн.. Гравець придбав s білетів. Знайти ймовірність того, що він придбав виграшні білети однакового номіналу з виграшем не більше 20 грн.
а) m=100, n=1, k=3, r=6, p=15, s=2
б) m=250, n=2, k=5, r=15, p=25, s=3
в) див. рекомендації до виконання завдань
10. В лабораторії знаходяться m кролів, з них носіїв вірусу В1 – n, носіїв вірусу В2 – k, носіїв вірусу В3 – r. Навмання взято s кролів. Знайти ймовірність того, що всі вони носії однакового вірусу.
а) m=20, n=5, k=5, r=7, s=3 б) m=100, n=15, k=25, r=20, s=3 в) див. рекомендації до виконання завдань
11. Екзаменаційні роботи абітурієнтів зашифровані номерами від 1 до n. Навмання вибираються m робіт. Знайти ймовірність того, що номери цих робіт діляться на 10 або на 11.
а) n=100, m=2 б) n=200, m=5 в) див. рекомендації до виконання завдань
12. З колоди на n карт навмання виймають m карт. Знайти ймовірність того, що всі вони будуть одного кольору.
а) n=36, m=8 б) n=52, m=5 в) див. рекомендації до виконання завдань
13. В урні знаходяться m білих та n чорних куль. Що ймовірніше витягнути k білих чи r чорних куль?
а) m=6, n=3, k=3, r=2 б) m=100, n=50, k=50, r=25 в) див. рекомендації до виконання завдань
14. У лабораторії працюють m жінок та n чоловіків. k людей повинні їхати у відрядження. Знайти ймовірність того, що у відрядження поїдуть люди однакової статі.
|
|
|
а) m=10, n=7, k=2 б) m=20, n=10, k=5 в) див. рекомендації до виконання завдань
15. В ящику знаходяться m банок І сорту, n банок ІІ сорту і k банок ІІІ сорту. Знайти ймовірність того, що серед вибрані навмання всі r банок будуть одного сорту.
а) m=10, n=15, k=7, r=2 б) m=40, n=25, k=30, r=10 в) див. рекомендації до виконання завдань
ЗАВДАННЯ 2.
1. Президент фірми хоче створити команду дизайнерів для розробки нової моделі товару у складі інженерів і спеціалістів дослідження ринку. Знайти ймовірність того, що команда такого складу буде створена, якщо з групи m інженерів і n спеціалістів з проблем ринку вибирати навмання k осіб, серед яких не менше r інженерів.
а) m=10, n=5, k=5, r=3 б) m=50, n=15, k=9, r=7 в) див. рекомендації до виконання завдань
2. Інвестиційна компанія має m пакетів акцій, серед яких n пакетів цукрових заводів. Знайти ймовірність того, що серед навмання вибраних k пакетів більше r пакетів цукрових заводів.
а) m=20, n=8, k=5, r=3 б) m=80, n=15, k=10, r=7 в) див. рекомендації до виконання завдань
3. За списком групи є m дівчат і n хлопців. Навмання по одному називають по журналу номери k студентів. Знайти ймовірність того, що серед них не менше r хлопців.
а) m=16, n=9, k=3, r=2 б) m=20, n=25, k=4, r=2 в) див. рекомендації до виконання завдань
4. Студент знає m із n питань програми з фізики. Знайти ймовірність того, що він відповість не менше, ніж на k з r поставлених викладачем питань.
а) m=50, n=60, k=2, r=3 б) m=100, n=200, k=4, r=5 в) див. рекомендації до виконання завдань
5. Із комплекту, в якому m якісних деталей і n деталей з дефектами, навмання вибирають r деталей. Знайти ймовірність того, що хоча б k деталей будуть якісними.
а) m=25, n=10, k=2, r=3 б) m=50, n=30, k=3, r=4 в) див. рекомендації до виконання завдань
6. З колоди у n карт довільно вийняли 3 карти. Знайти ймовірність того, що це 2 валети і десятка одного кольору.
а) n=36, m=3 б) n=52, m=3 в) див. рекомендації до виконання завдань
7. У лабораторії працюють n жінок і m чоловіків. k людей повинні їхати у відрядження. Знайти ймовірність того, що у відрядження поїде не менше r жінок.
а) m=12, n=8, k=5, r=4 б) m=50, n=30, k=7, r=5 в) див. рекомендації до виконання завдань
8. В ящику лежать m ламп потужністю 40 вт, n ламп потужністю 60 вт і k ламп потужністю 100 вт. Навмання виймають r ламп. Знайти ймовірність того, що серед них не менше s ламп потужністю 100 вт.
а) m=20, n=10, k=15, r=4, s=3 б) m=50, n=30, k=20, r=5, s=3 в) див. рекомендації до виконання завдань
9. До коробки з m новими ручками поклали n ручок, в яких вже немає пасти. Знайти ймовірність того, що серед k навмання взятих ручок будуть принаймні r нових.
а) m=10, n=5, k=3, r=2 б) m=50, n=10, k=7, r=5 в) див. рекомендації до виконання завдань
10. В ящику знаходяться m м’ячів, серед яких n нових. Для першої гри вибирають 3 нові м’ячі, які після гри повертаються в ящик. Для другої гри вибирають навмання k м’ячів. Знайти ймовірність того, що серед них хоча б r нових.
а) m=15, n=9, k=3, r=2 б) m=50, n=10, k=7, r=5 в) див. рекомендації до виконання завдань
11. В ящику знаходиться m консервних банок І сорту і n банок ІІ сорту. Для контролю навмання вибирають k банок. Знайти ймовірність того, що серед вибраних банок буде більше r банок ІІ сорту.
а) m=8, n=7, k=6, r=4 б) m=50, n=30, k=10, r=8 в) див. рекомендації до виконання завдань
12. Із m білетів є n виграшних. Знайти ймовірність того, що серед навмання взятих k білетів не більше r виграшних.
а) m=16, n=6, k=7, r=1 б) m=50, n=10, k=8, r=2 в) див. рекомендації до виконання завдань
13. На полиці у випадковому порядку стоять m підручників, причому n з них з алгебри. Бібліотекар бере навмання k підручники. Знайти ймовірність того, що хоча б r підручники з алгебри.
а) m=15, n=5, k=3, r=2 б) m=50, n=30, k=8, r=6 в) див. рекомендації до виконання завдань
14. Екзаменаційні роботи абітурієнтів зашифровані номерами від 1 до n. Навмання вибираються k роботи. Знайти ймовірність того, що номери хоча б r з цих робіт діляться на 10.
а) n=100, k=3, r=2 б) n=1000, k=8, r=6 в) див. рекомендації до виконання завдань
15. З урни, що містить m білих і n чорних куль навмання вибирають k кулі. Знайти ймовірність того, що серед вибраних куль не менше r білої.
а) m=4, n=6, k=3, r=1 б) m=50, n=30, k=8, r=6 в) див. рекомендації до виконання завдань
