Политропические процессы

Адиабатический процесс. Это процесс, который происходит без теплообмена с окружающей средой. Для идеального газа дифференциальную форму первого начала термодинамики за­пишем с учетом выражения для внутренней энергии в виде

 

 

Выпишем числитель этого выражения:

 

После сокращения на р dV получим

Разделим оба слагаемых на pV, тогда

 

 

Это выражение представляет собой сумму дифференциалов ло­гарифмов р и V:

 

 

Равенство нулю последнего дифференциала означает, что мы имеем дело с константой, т. е.

 

Это и есть уравнение адиабаты в переменных р, V. Его называ­ют уравнением Пуассона. Это уравнение можно представить и в других переменных. Например, в переменных Т, V оно выгля­дит так:

 

Адиабата pV идет круче изотермы pV = const.

 

 

Политропические процессы. Так называют процессы, урав­нение которых в переменных р, V имеет вид

 

где п — произвольное число, как положительное, так и отрица­тельное, а также равное нулю. Таким образом, любой процесс, уравнение которого можно свести к этому виду, является полит­ропическим. Соответствующую кривую называют политропой.

Политропическими являются, в частности, процессы изохорический, изобарический, изотермический и адиабатический.

Отличительной особенностью всех политропических процес­сов является то, что входе этих процессов теплоемкость систе­мы остается постоянной:

 

Если п = , то С _п = 0 (это сразу следует и из определения ади­абатического процесса). При п = 1 С _п → 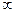, как и должно быть при изотермическом процессе.

Интересный результат обнаруживается в случае 1 < п < , Перепишем выражение для С_n в виде

 

 

Видно, что в этом случае С_п < 0. Это значит, что сообщается тепло сис­теме, а она охлаждается, поскольку знаки d'Q и dT должны быть при этом противоположными. Это отно­сится ко всем политропическим про­цессам, «промежуточным» между изотермическим и адиабатическим

 

 

 

Нетрудно получить выражение, определяющее п через теплоемкости: