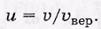Формула Максвелла в приведенном виде

Решение ряда задач удобнее проводить, если выражать ско­рости v молекул в относительных единицах — единицах наибо­лее вероятной скорости v_вер. Тогда относительная скорость мо­лекулы

При переходе к распределению по другой переменной (здесь от к u) будем исходить из вероятности d P пребывания моле­кулы в интервале скоростей (, + d ), которая равна dР = = F()d . Значение этой вероятности не изменится, если правую часть равенства разделить и умножить на du. Тогда можно за­писать

Таким образом, мы переходим от интервала (, + d ) к соот­ветствующему ему интервалу (u, u + du).

Так как = u _вep и d /du = u_вер. После преобразований и подстановке в выражение для dP получим

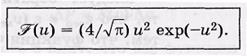
В таком виде распределение Максвелла является универсаль­ным: оно не зависит ни от температуры, ни от рода газа.

Пример. Найдем относительное число молекул dN/N со скоростями, отличающимися от наиболее вероятной не более, чем на = 1%.

В данном случае u = 1, и мы можно записать

где du = 2 |, поскольку на % отклонения могут быть как в одну, так и в другую сторону.