Распределение молекул по модулю скорости

Найдем вероятность или относительное число молекул, мо­дуль скорости которых заключен в интервале (, + d ). Таким молекулам соответствуют все точки, попадающие в шаровой слой с радиусами и + d .

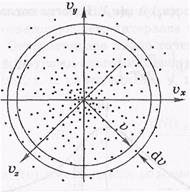
Объем этого слоя равен произведению поверхности слоя на его толщину, т. е. 4π ²d , объемная же плотность вероятности f() во всех точках слоя одинакова.

Следовательно, согласно теореме сложения вероят­ностей, вероятность попадания в этот слой

Величина dP/d — мы ее обозначим F() — характеризует искомую вероятность, т.е.

Учитывая формулу для f(), получим:

Эта формула представляет собой закон распределения Макс­велла по модулю скорости. Вид функции F() показан на следующем рисунке.

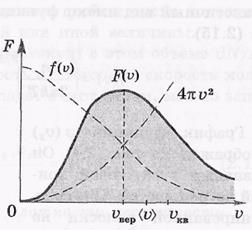
Эта функция тоже нормирована на единицу:

На рисунке пунктиром представлены сомно­жители функции F(), один из сомножителей которой f(). Площадь под кривой f() физиче­ского смысла не имеет.

Следует отметить, что полученные Максвеллом распределе­ния по скоростям не зависят ни от структуры молекул, ни от того, как они взаимодействуют друг с другом. Поэтому они применимы не только к газам, но и к другим агрегатным состо­яниям вещества.

Характерные скорости. К ним относятся три скорости: наи­более вероятная _вер, средняя < > и среднеквадратичная _кв.

Наиболее вероятной скорости соответствует максимум фун­кции распределения F(). Эта скорость определяется из усло­вия dF/d = О, откуда следует

Средняя скорость по определению

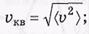
Среднеквадратичная скорость

она находится из условия

откуда следует, что

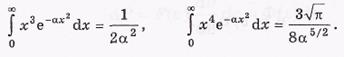Этот результат можно получить путем интегрирования, используя табличные значения интегралов:

В качестве примера приведем среднюю скорость молекул азота N₂ при Т = 300 К: <v>» 480 м/с. Эта величина имеет поря­док скорости звука в азоте, v_зв = 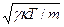= 350 м/с.

Приведенные характерные скорости отличаются друг от друга в пропорции

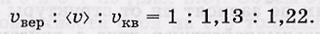
Зависимость распределения от Т. Подставив значение _вер и формулу F(), получим, что

В соответствии с этим результатом для разных температур Т₁ < Т₂ < Т3 кривые распределения F(v) будут иметь вид, пока­занный на следующем рисунке.

Видно, что с увеличением Т максимум фун­кции F() смещается в сторону больших скоростей, а его вели­чина уменьшается. При этом площадь под все­ми тремя кривыми остается равной единице. Кривые на этом рисунке можно рассматривать и иначе — как соответствующие разным массам молекул газа при одной и той же температуре, причем m₁ > m₂ > m₃.