Барометрическая формула

Умножив обе части распределения Больцмана на kT, получим давление на высоте z

 

где М — молярная масса, R — универсальная газовая постоянная.

Это так называемая барометрическая формула. Она строго спра­ведлива для идеального газа, температура которого не зави­сит от высоты (изотермическая атмосфера). На рисунке пока­заны два графика барометрической формулы при разных температурах: Т₂ > Т₁.

 

 

В отличие от распределе­ний n(z) кривые p(z) на этом рисунке начинаются в одной точке, независимо от температуры.

Явления переноса

Выведенная из состояния равновесия, любая макросистема стремится вернуться в равновесное состояние. При этом растет энтропия, значит этот процесс необратим. Нарушение равнове­сия сопровождается возникновением потоков или частиц, или тепла, или электрического заряда и др. Соответствующие про­цессы называют явлениями переноса. Все они являются необра­тимыми.

Рассмотрим три явления переноса: диффузия, внутреннее трение и теплопроводность (причем в условиях, когда отклонения от равновесия малы). Сначала приведем эмпирические уравнения этих процессов — они применимы к любым средам (газообразным, жидким и твердым). Затем полу­чим молекулярно-кинетический вывод данных уравнений для газов, который позволяет раскрыть содержание коэффици­ентов, характеризующих соот-ветствующие явления.

В дальнейшем придется использовать понятие потока той или иной физической величины через интересующую нас поверхность S. Напомним, поток — величина скалярная и алгеб­раическая. Его знак зависит от выбора положительного «на­правления»; с одной стороны поверхности S к другой или нао­борот. Положительное направление обычно выбирают произвольно (за исключением замкнутых поверхностей, где по соглашению его выбирают наружу области, ограниченной этой поверхностью).

Мы будем рассматривать потоки в основном через плоские поверхности S, перпендикулярные оси X, выбирая положите­льное «направление» поверхности S совпадающим с ортом оси X. Если физическая величина будет переноситься через S в на­правлении оси X, будем считать соответствующий поток поло­жительным, если же в обратном направлении, то — отрицате­льным.

Любое явление переноса связано с неодинаковостью в про­странстве некоторой величины. Например, поток тепла возника­ет в случае неодинаковости температуры в разных точках среды. На эту особенность потоков следует обратить внимание. Та же температура — это характеристика системы в целом, а здесь мы говорим, что она разная. Приходится вводить понятие локально­го равновесия. В состоянии локального равновесия среда в каж­дой малой части своего объема находится в тепловом равнове­сии, однако равновесие между различными частями отсутствует.

Под малостью имеют в виду объем, размер которого намного превышает, например, среднее расстояние между соседними молекулами. При этом число частиц в таком объеме должно быть макроскопическим, чтобы можно было применять макро­скопические параметры состояния теплового равновесия.

Теперь перейдем к эмпирическим уравнениям процессов пе­реноса.

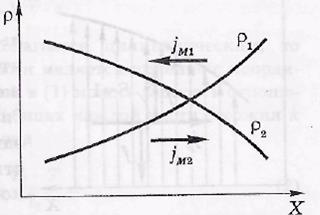Диффузия. Так называют взаимопроникновение вещества в различных смесях, обуслов­ленное тепловым движением молекул. Пусть смесь содержит две компоненты с парциальны­ми плотностями ρ₁ и ρ₂. Концентрация каждой компоненты стремится выравняться, возникают потоки массы обеих компонент, направленные в сторону уменьшения их плотностей. Экспериментально было установлено выраже­ние для плотности потока массы i-й компоненты:

 

где D — коэффициент диффузии. Знак минус обусловлен тем, что поток i-й компоненты противоположен производной dρ/dх — ее называют градиентом плотности (см. риcунок).

Внутреннее трение. Из механики известно, что сила трения между двумя слоями жидкости или газа, отнесенная к единице площади поверхности раздела слоев, равна

 

 

где -коэффициент вязкости (вязкость), производная du/dх — градиент скорости — характеризует степень измене­ния скорости жидкости или газа в направлении оси X, перпен­дикулярном направлению движения слоев.

Согласно 2-му закону Ньютона взаимодействие двух слоев с силой f можно рассматривать как процесс передачи в единицу времени импульса. Тогда предыдущее уравнение можно представить так

 

 

где j_p — импульс, передаваемый ежесекундно от слоя к слою через единицу площади поверхно­сти, т. е. плотность потока импу­льса. Знак минус обусловлен тем, что поток импульса противополо­жен по направлению градиенту du/dх. На следующем рисунке пока­заны силы, действующие в плоско­сти площадки S:

 

левая f — сила, с которой действуют слои справа от площадки S (они движутся в дан ном случае быстрее), правая f — сила, с которой действуют слои слева от S. Эти силы взаимно противоположны и одинако­вы по модулю. Вопрос, куда действует сила в плоскости S, не имеет смысла, пока не указано, со стороны каких слоев на ка­кие.

Теплопроводность. Опыт показывает, что если в среде со­здать вдоль оси градиент температуры dТ/dх, то возникает по­ток тепла, плотность которого

 

 

где - коэффициент теплопровод­ности (теплопроводность). Знак минус стоит по той же причине: плотность потока противоположна по направлению градиенту dТ/dх.

 

Молекулярно-кинетическая интерпретация явлений переноса

Рассмотрим явления переноса в газах с молекулярно-кинетической точки зрения.

Ввиду полной хаотичности теп­лового движения молекул будем считать, что молекулы дви­жутся по трем направлениям X, Y и Z, так что на каждое направление в одну сторону плотность потока молекул состав­ляет

 

 

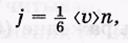
где п — концентрация молекул. Эти потоки и являются пере­носчиками определенных физических величин G. Плотность потока величины G будем обозначать J_G.

Далее будем считать, что через интересующую нас площадку S молекулы будут переносить то значение величины G, которое они имели на расстоянии λ, от площадки S. Т. е. будем предпо­лагать, что последнее соударение молекулы испытывают на этом расстоянии от S.

Общее уравнение переноса. Пусть величина G характеризу­ет определенное молекулярное свойство, отнесенное к одной молекуле. Это может быть энергия, импульс, электрический за­ряд и др. Ясно, что при наличии градиента величины G должен возникнуть поток в сторону ее уменьшения.

Пусть величина G меняется то­лько в направлении оси X, напри­мер, так, как показано на рисунке

 

 

Площадку S будут пронизывать молекулы, движущиеся во встреч­ных направлениях, их плотности потоков обозначим j' и j". Причем
они должны быть равны друг другу (j' = j"), что­бы не возникало газодинамических потоков и чтобы все процессы сводились только к переносу величины G. Тогда для результирую­щей плотности потока величины G можно запи­сать:

 

Благодаря малости λ разность значений G"- G' представим в виде

 

 

С учетом этой формулы выражение для J_G. запишем так:

 

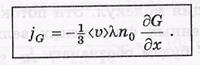
Это и есть общее уравнение переноса для любой величины G. Здесь п_о — концентрация молекул, < > — их средняя тепловая скорость. Значения этих величин берутся в сечении S.

Применим это уравнение к трем наиболее интересным явле­ниям переноса, связанным с диффузией, вязкостью и теплопро­водностью.

Диффузия. Ограничимся рассмотрением самодиффузии, т. е. процессом перемешивания (взаимопроникновения) моле­кул одного сорта. Макроскопически самодиффузию наблюдать нельзя: из-за тождественности молекул она не может проявля­ться ни в одном явлении. Для наблюдения этого процесса часть молекул газа надо как-то «пометить». Практически это можно сделать с помощью так называемых «меченых» атомов: смесь газов берут из двух изотопов одного и того же элемента, один из которых радиоактивен. Тогда процесс диффузии можно на­блюдать, регистрируя радиоактивное излучение радиоизотопа. Можно также взять смесь двух различных газов, молекулы ко­торых почти одинаковы по массе и размерам (такие, например, как N₂ и СО). В этом случае у обеих компонент газа будут оди­наковы как средние скорости, так и длины свободного пробега, т. е. <v> и λ.

Чтобы отсутствовали газокинетические потоки b перемеши­вание молекул происходило только за счет диффузии, необходимо (так мы и будем считать), чтобы суммарная концентра­ция п₀ обеих компонент смеси не зависела от координаты в направлении оси X, вдоль ко­торой происходит этот процесс (рисунок).

 

Пусть концентрация моле­кул 1-го сорта зависит от коор­динаты х как n₁(x). Учитывая,что величина G есть характеристика перено­симого количества, отнесенного к одной молекуле, имеем

 

где п₀ — равновесная концентрация. Тогда общее уравне­ние переноса примет вид

 

Сравнив это выражение с эмпирической формулой для плотности потока массы, на­ходим, что коэффициент самодиффузии

 

 

Единицей измерения коэффициента D является м²/с. При нормальных условиях коэффициент D для кислорода и азота в воздухе имеет порядок 10^-5 м²/с.

Мы ограничимся рассмотрением самодиффузии, поскольку взаимная диффузия разных газов требует весьма громоздких преобразований, но принципиально нового ничего не дает.

Вязкость (внутреннее трение). Это явление возникает в техслучаях, когда на хаотическое тепловое движение молекул на­кладывается упорядоченное движе­ние.

Пусть скорость u упорядочен­ного движения зависит только от координаты х, как показано на рисунке

 

 

В этом случае через единич­ную площадку S будет происходить перенос импульса р = mu, где m —масса молекулы. Это значит, что в
данном случае величина G = р и плотность потока импульса

 

где ρ = mп₀ — плотность газа. Сопоставив это уравнение с эмпи­рической формулой, находим выражение для вязкости:

 

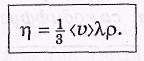
Более точный расчет дает несколько большее значение для числового коэффициента: не 1/3, а 0,49.Единицей вязкости в СИ является паскаль-секунда (Па-с), а в системе СГС — пуаз (П). Связь между ними: 1 Па-с = 10 П.

При нормальных условиях вязкость газов - 10^-5 Па-с.

Теплопроводность. В этом явлении величиной G яв­ляется средняя энергия теплового движения, приходящаяся на одну молекулу. Из теоремы о равнораспределении энергии по степеням свободы имеем G = (i/2)kT, и тогда плотность потока тепла

 

 

Для упрощения этой формулы введем удельную теплоемкость c_v. Для этого обратим внимание на то, что (i/2)k — это теплоемкость при постоянном объеме, рассчитанная на одну молекулу. Произведение данной величины на концентрацию п₀ дает теп­лоемкость единицы массы c_v, умноженную на плотность газа ρ. Таким образом, учитывая, что (i/2)k-n₀ = c_vρ,

 

Из сравнения этого выражения с эмпирической формулой получим, что теплопроводность

 

 

где c _v — удельная теплоемкость, отнесенная к еди­нице массы, Дж/К۰кг).

Единицей теплопроводности является Вт/(м۰К).

При заданной концентрации п₀ теплопроводность зависит в основном от средней скорости < > Из-за этого легкие газы обла­дают значительно большей теплопроводностью, чем тяжелые, поскольку < > ~ 1/ . Например, при нормальных условиях кислород имеет теплопроводность 0,024 Вт/(м۰К), а водород — 0,176 Вт/м۰К).

Анализ коэффициентов переноса. Прежде всего выпишем для удобства сопоставления и анализа все три коэффициента рассмотренных явлений переноса:

 

1. Определив по эмпирическим формулам коэффициенты D, и , мы имеем возможность вычис­лить и диаметр d молекул.

2.Все три коэффициента, D, и , с ростом температуры Т увеличиваются, так как < >~ .

3.Поскольку ~ 1/ п, а п ~ ρ, то как вязкость , так и теп­лопроводность не зависят от концентрации, а значит и от давления (при неизменной температуре).

 

Уравнения переноса, зависящие от времени. Приведенные выше расчеты и результаты относятся к так называемым стационарным за­дачам, когда распределение интересующей нас величины G зависит то­лько от координат. Но процессы переноса (выравнивания величины G) зависят и от времени. Это обстоятельство приводит к необходимости решать нестационарные задачи, учитывающие зависимость величины G как от координат, так и от времени. В качестве примера приведем соответствующее одномерное дифференциальное уравнение для тепло­проводности:

Для решения подобных уравнений необходимо знать начальные и гра­ничные условия. Если они заданы и известен коэффициент , то задача является чисто математической, ее решение подробно рассматрива­ется в курсе математической физики.

Реальный газ

Уравнение Ван-дер-Ваальса. При увеличении давления (при Т = const) оказывается, что pV RТ. При р = 1000 атм произведение pV ста­новится вдвое больше, чем предписывает модель идеального газа (газ не «сжимается»).

Причин этому две:

собственный размер молекул; он и уменьшает объем, до­ступный для движения молекул, при нормальных условиях он составляет ~ 0,07 % объема сосуда с газом, а при 100атм уже 70%; сложный характер взаимодействия между молекулами.
Типичная кривая зависимости энергии взаимодействия U_B3 от расстояния r между их центрами приведена на рисунке. На малых расстояниях (г < г₀) молекулы от­талкиваются, на больших (г > г₀) притягиваются.

 

Эти причины можно учесть пу­тем введения поправок в уравнение состояния идеальных газов, что и выполнил Ван-дер-Ваальс.В результате уравнение состояния одного моля реального газа приняло вид

 

Это и есть уравнение Ван-дер-Ваальса. Здесь а и b — посто­янные Ван-дер-Ваальса, для разных газов они имеют свои зна­чения.

Если мы имеем дело не с одним, а с молями газа объемом V, то в уравнении вместо объема одного моля V_M,следует подставить V / .

Поправка в первой скобке, , обусловлена силами при­тяжения между молекулами. Она имеет размерность давления, и ее иногда называют внутренним давлением. На стенку сосу­да такой газ оказывает давление р. Однако, если бы силы при­тяжения между молекулами мгновенно исчезли, то давление на стенку стало бы p + a /V²_M. т. е. при переходе от идеального газа к реальному давление на стенку уменьшается — из-за сил притяжения между молекулами.

Поправка b связана с собственным объемом молекул, ее размерность м³/моль.

Газ, подчиняющийся данному уравнению называют ван-дер-ваальсовским.

Энергия ван-дер-ваальсовского газа. Внутренняя энергия такого газа U = К + U_вз, где К — суммарная кинетическая энер­гия молекул, U_вз — суммар­ная энергия взаимодействий молекул (собственная потенциаль­ная энергия). Сначала найдем U_вз. Для этого воспользуемся тем, что работа сил притяжения равна убыли энергии U_вз: dA = - dU_вз. Силы притяжения характеризуются внутренним дав­лением p_i = a / V². Тогда элементарная рабо­та этих сил d'A =- p_idV, где знак минус обусловлен тем, что при расширении газа (dV > 0) работа d'A должна быть отрица­тельной, т.е. d'A < 0. Итак,

-

 

Мы представили d'A как убыль некоторой величины — она и является энергией U_вз:

 

 

Константа, которую здесь следовало бы добавить, несущест­венна. Поэтому мы сразу же положили ее равной нулю. Полу­чается естественный результат: при V→ 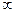U_вз→ 0.

Суммарная кинетическая энергия К зависит от поступа­тельного и внутреннего движений молекул, и определяется как C_VT

Таким образом, внутренняя энергия моля ван-дер-ваальсов­ского газа

 

где C_V =(i/2)R.

Если газ расширяется в пустоту без теплообмена с окружаю­щими телами, то А = 0, Q = 0, и согласно первому началу в этом процессе U = const. Значит, с ростом объе­ма температура газа уменьшается (в отличие от идеального газа).

Это можно представить и наглядно на рисунке. Видно, что при расширении газа (увеличении объема V) в случае U = const суммарная кинетическая энергия мо­лекул газа, а значит и температура Т, уменьшается. Газ охлаждается.

 

Эффект Джоуля—Томсона. Исследования Джоуля и Томсона позво­лили не только экспериментально подтвердить зависимость внутрен­ней энергии реального газа от его объема. Было открыто важное физи­ческое явление, получившее название эффекта Джоуля-Томсона.

В их опытах использовалась теплоизолированная трубка, в середи­не которой помещалась пористая перегородка N.

 

Исследуе­мый газ под действием перепада давлений (p₁>p₂) медленно протекал через перегородку. Благодаря медленности течения кинетическая энергия газа как цело­го практически не менялась. В этих условиях газ в каждый момент по обе стороны перего­родки находился в термодинамически равно­
весных состояниях. Теплоизолированность трубки делала процесс течения адиабатиче­ским. Давления газа по обе стороны перегородки (p₁ и р₂) поддержива­лись постоянными.

При стационарном течении с одной стороны перегородки устанав­ливалась постоянная температура Т₁, а с другой стороны — Т₂. Эти температуры и измерялись в опытах. Изменение температуры — при­ращение T — при таком течении и называют эффектом Джоуля-Томсона.

Сначала попытаемся выяснить, что можно ожидать относитель­но T. Для этого мысленно выделим слева от перегородки объем V₁ моля газа. После прохождения через перегородку эта порция газа займет объем V₂. Согласно 1-му началу термодинамики с учетом того, что в этом процессе Q = 0, приращение внутренней энергии U данной порции газа равно работе А' внешних сил:

 

При малом перепаде давлений

 

 

где U _вз — приращение энергии взаимодействия моля молекул газа. Имея в виду, что U = А', получим из двух предыдущих формул, что

 

 

Из этой формулы следует, что эффект (знак T) за­висит от соотношения между приращени­ем внутренней энергии U, равной работе
внешних сил, и приращением энергии взаимодействия U_вз. Это поясняет рисунок,

 

 

где величина вертикального отрезка характеризует собственную кинетическую энергию газа К, а значит и температуру Т. В частности, если U = U_вз, то T = 0.

Довольно громоздкий расчет дает возможность найти зависимость давления р1 от Т₁ при которых эффект ( T) равен нулю. Соответству­ющая зависимость р₁(T₁) — ее называют кривой инверсии — показана на рисунке.

 

Начальные состояния (р₁Т₁) под кривой инверсии при­водят к положительному эффекту Джоуля-Томсона, т. е. к охлаждению газа ( T < 0), Кривая инверсии не является универсальной, она своя для каждого газа, поскольку расчетная формула для T зависит от постоянных а и b Ван-дер-Ваальса.

 

 

Температура. Это величина, характеризующая состояние термодинамического равновесия макросистемы. Если при уста­новлении теплового контакта между телами одно из тел переда­ет энергию другому посредством теплопередачи, то считают, что первое тело имеет большую температуру, чем второе.

Любой метод измерения температуры требует установления температурной шкалы. Для этого используют некоторые осо­бые точки. По международному соглашению температурную шкалу строят по одной реперной точке, так называемой трой­ной точке воды (Ттр). В термодинамической шкале темпера­тур (шкале Кельвина) принимается по определению, что

 

 

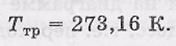
При таком значении Ттр интервал между точками плавления льда и кипения воды практически равен 100 кельвин, и темпе­ратуры этих точек равны приближенно 273,15 и 373,15 К. На­помним, 1 К = 1°С. Температура t по шкале Цельсия связана с температурой по шкале Кельвина равенством

 

 

Температуру Т = 0 называют абсолютным нулем, ему соот­ветствует t = -273,15 °С.

Состояние системы. Состояние макросистемы характеризу­ют величинами, которые называют термодинамическими пара­метрами (давление р, объем V, температура Т и др.). Если эти параметры имеют определенные и постоянные значения для любой части макросистемы, то ее состояние называют равновес­ным. Будучи выведена из состояния равновесия (система стано­вится неравновесной), система в дальнейшем возвращается в равновесное состояние. Это происходит за время, равное по по­рядку величины времени релаксации (т). Так называют время, за которое первоначальное отклонение какого-либо параметра состояния уменьшается в е раз. Для каждого параметра состоя­ния время т имеет свое значение. Решающую роль играет то т, которое является наибольшим. Его и считают за время релак­сации системы.

Таким образом, состояние системы является равновесным, если все параметры ее имеют определенные и постоянные зна­чения при неизменных внешних условиях.

Равновесное состояние можно представить точкой в про­странстве, по координатным осям которого откладываются зна­чения параметров состояния. Если независимыми являются всего две переменные (например, р и V), то равновесное состоя­ние изображают точкой на диаграмме р, V.

Процесс. Любой процесс, т.е. переход системы из одного со­стояния в другое (происходящий, например, благодаря внешне­му воздействию) проходит, вообще говоря, через последовате­льность неравновесных состояний. Но
если такое воздействие осуществляется
достаточно медленно, то можно ска­зать, что процесс проходит через по­следовательность равновесных состоя­ний. Такой процесс называют равно­весным или квазистатическим. Он
может быть изображен, например, на
диаграмме р, V соответствующей кривой.

 

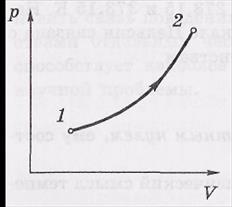
Направление процесса показывают стрелкой.

Неравновесные процессы мы будем условно изображать пун­ктирными кривыми.

Равновесный процесс может быть проведен в обратном на­правлении через ту же совокупность равновесных состояний, т. е. по той же кривой 1→2, но в обратном направлении 2→1. По этой причине равновесные процессы на­зывают обратимыми.