Лекция 5. ОПТИМАЛЬНЫЙ ПОРТФЕЛЬ
Применим теорему множителях Лагранжа к решению задачи составления портфеля для осторожного инвестора при разрешении взятия ценных бумаг в долг без покрытия.
5.1. Запишем задачу составления оптимального портфеля в стандартной форме задачи нелинейного программирования:
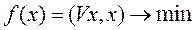
при ограничениях
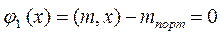
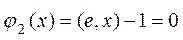
Так как у нас два равенства, то и множителей Лагранжа будет два, таким образом:
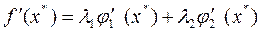
Рассчитаем градиенты функций - ограничений к целевой функции:
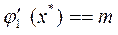
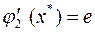
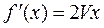
По теореме 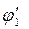 и
и 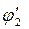 должны быть линейно - независимыми, предположим противное, то есть, что существует такое k, что выполняется равенство:
должны быть линейно - независимыми, предположим противное, то есть, что существует такое k, что выполняется равенство:
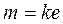
или в скалярной форме:
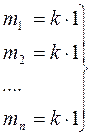
Таким образом m1=m2=...=mn, следовательно для линейной независимости необходимо, чтобы эффективности хотя бы двух видов ценных бумаг отличались друг от друга. Очевидно, что это общий случай, который будем предполагать выполненным.
Тогда из теоремы о множителях Лагранжа с учетом ограничений получаем систему из n+2 уравнений с n+2 неизвестными 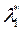 ,
, 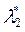 , x*:
, x*:
|
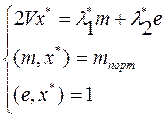
 2014-01-28
2014-01-28 705
705








