Теорема 2 (Зависимость риска от эффективности)

Тогда,

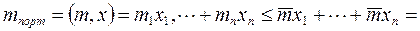
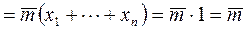
Следовательно,

,

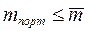что противоречит предположению и доказывает теорему.

Теорема доказана.

Замечание3. Предыдущее условие является необходимым, но не достаточным условием, а именно, при формировании некоторых портфелей с эффективностью меньше, чем максимальная все равно может иметь место взятие ценных бумаг в долг, но уже с целью уменьшения риска.

С увеличением эффективности портфеля риск увеличивается, причем если 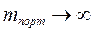, то и риск .

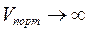Доказательство:

Нужно доказать, что

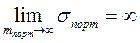
Рассчитаем зависимость риска от эффективности. Для этого решим систему уравнений:

(43)

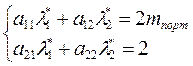
Так как решение линейной системы уравнений от линейно входящих параметров зависит линейно, то

(44)

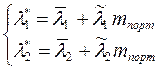
где 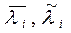- некоторые числа.

Подставим соотношения (44) в систему (43), приведем подобные и приравняем выражения слева и справа.

Получаются следующие системы уравнений относительно 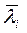и :

(45)

(46)

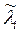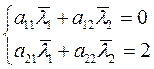
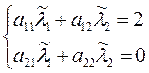
Решим систему (46)

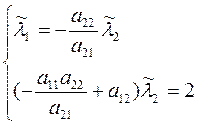
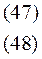
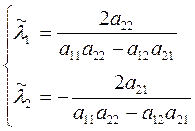
Введем обозначение:

,

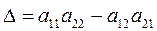тогда

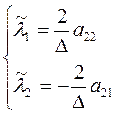
Из равенств (44) получаем:

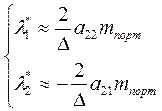
Рассчитываем теперь риск портфеля:

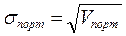
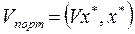
вспоминая, что

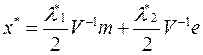
получим,

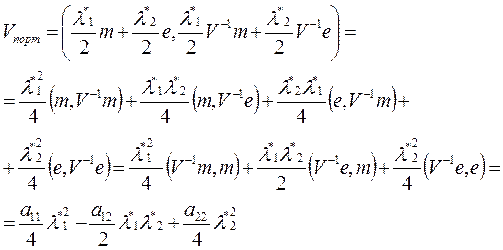
Подставим оценки для 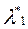и 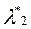и получим:

,

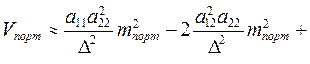
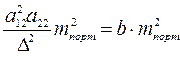где

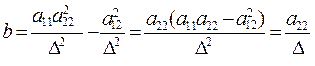
Таким образом мы получили:

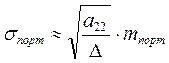
и следовательно

,

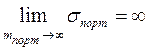что и требовалось доказать.

Теорема доказана.