Дискретное и быстрое преобразование Фурье

Среди прямых можно выделить алгоритмы с непосредственным вычислением выражения (13.5) и быстрые прямые алгоритмы (БПА), которые позволяют для некоторых частных случаев (четных значений, периодический последовательностей и др.) уменьшить требуемые вычислительные затраты [3].

Большое распространение получили алгоритмы на основе обобщенного дискретного преобразования Фурье, которые объединяют широкую совокупность алгоритмов, использующих: дискретное преобразование Фурье; теоретико-числовое преобразование [3,9]; полиноминальную алгебру [1]; специальные методы; комбинацию перечисленных алгоритмов.

В цифровой обработке сигналов обобщённое дискретное преобразование Фурье имеет важное значение не только в связи с вычислением цифровых свёрток, но и в ряде других приложений, причём наиболее полно его аппарат разработан для метода дискретного преобразования Фурье (ДПФ). Последний представляет собой специальную версию общего Фурье-преобразования, позволяющего представить сигналы в виде суперпозиции гармонических функций и подробно рассмотренного во многих литературных источниках, например [6,11,13]. ДПФ, описываемое парой соотношений (прямым и обратным):

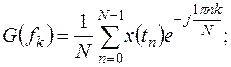(13.6)

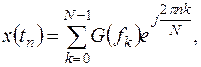(13.7)

где 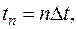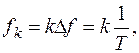выполняет блочный анализ временного сигнала.

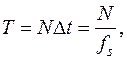
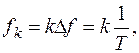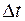Блок состоит из отсчётов входного процесса, что соответствует длине реализации где и 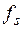- период и частота дискретизации. При этом в ДПФ подразумевается, что анализируемый блок является одним из периодов бесконечной периодической функции. Соответственно, получаемый частотный спектр (т.е. зависимость амплитуд и фаз гармонических составляющих сигнала от частоты) будет линейчатым, т.е. состоящим из отдельно расположенных вдоль частотной оси с интервалом 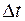линий, определяющих различные гармонические компоненты временного сигнала.

Если временная функция содержит только действительные значения, что является случаем, часто встречающимся на практике, то спектр сигнала является сопряжённой линейчатой функцией, т.е. компоненты положительной и отрицательной областей частот имеют одинаковые амплитуды, но противоположные фазы. Иначе говоря, только N/2 отсчётов в частотной области являются независимыми, а именно те, что расположены на отрезке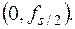

В общем случае при вычислении ДПФ от комплексной входной последовательности необходимо производить вычисление всех N спектральных компонент, так как в данном случае спектр не обладает свойством комплексно-сопряженной симметрии.

Ещё одна особенность ДПБ связана с представлением анализируемого сигнала как одного из интервалов бесконечной периодической функции. Если начальное и конечное значения сигнала на периоде различны, то в моменты времени 0, T, 2T,… происходит так называемый скачок функции, который может привести к существенному искажению спектра. Для устранения негативного влияния на спектр данной разрывности и получения лучшей избирательности необходимо использовать сглаживание с помощью одного из видов весовой функции (окна) [6,13]. Подробное описание различных окон, наиболее часто применяемых в гармоническом анализе методом ДПФ, представлено, например, в работе [16].

Возможность использования ДПФ при вычислении ЦС вытекает из фундаментального свойства преобразования Фурье, гласящего, что Фурье-образ произведения двух временных сигналов эквивалентен свёртке преобразований от каждого из сомножителей и, наоборот, свертка сигналов во временной области соответствует умножению их Фурье-отображений в частотной области [4, 5]. Поэтому возможно вычисление циклической (периодической) свёртки косвенным путём – посредством выполнения обратного преобразования Фурье от произведения ДПФ исходных периодических временных последовательностей. Такое решение имеет существенное практическое значение в том случае, когда преобразования могут быть выполнены быстрее, чем сама свёртка.

Эффективными процедурами вычисления ДПФ являются алгоритмы быстрого преобразования Фурье (БПФ), начало разработки которых было положено исследованиями Кули и Тьюки [19]. Общий принцип построения алгоритмов БПФ заключается в разложении процесса нахождения ДПФ на вычислении преобразований последовательностей меньшего размера. Действительно, как видно из выражения (13.6), суть ДПФ заключается в получении суммы произведений вида

(13.8)

где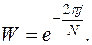

Весовая функция является периодической с интервалом N. Для заданного k при изменении n от нуля до N-1 произведение (13.8) также меняется периодически, причём число этих периодов равно k. Более того, даже в пределах одного периода могут образоваться комплексно-сопряжённые пары. Используя данные свойства, можно существенно уменьшить необходимое для вычислений число умножений. 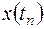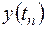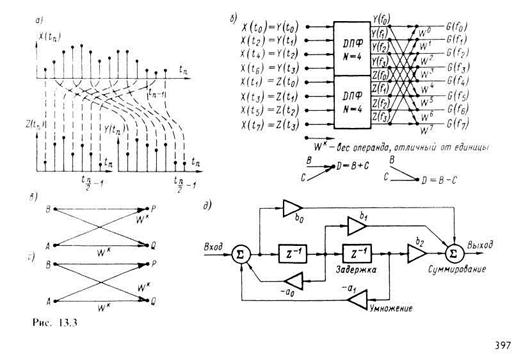Для этого входная последовательность разбивается на две вспомогательные последовательности - и 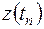(рис. 13.3, а) – так, что в 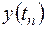попадают отсчёты только с чётными номерами, а в 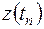- с нечётными, т.е.

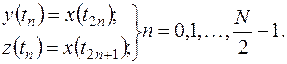
Тогда выражение (13.6) записывается

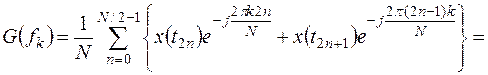
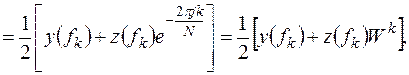(13.9)

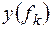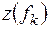где и - ДПФ последовательносте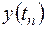й и 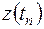соответственно.

Вычислительные затраты на реализацию N – точечного ДПФ в соответствии с выражением (13.9) составляют по 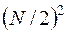операций на вычисление N/2 – точечных ДПФ 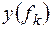и 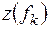и дополнительно N операций на их соединение, тогда как прямое вычисление 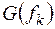по (13.6) требует 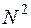операций, что почти в два раза больше.

В выражении (13.9) индекс k изменяется от 0 до N-1. Однако 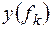и 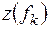имеют период N/2 и вычисляются только в диапазоне от 0 до N/2-1. Используя свойство периодичности функции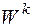

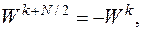
можно найти искомое соотношение и для 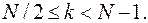Окончательно получаем [4]:

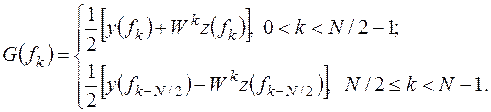(13.10)

Это соотношение между 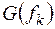, 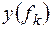и и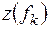зображено на рис 13.3,б, который показывает, как 8-точечное ДПФ сведено к двум 4-точечным.

Каждое из двух N/2 -точечных преобразований (если число их членов чётно) может быть найдено повторением указанного приёма, т.е. последовательност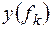и и 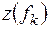снова разбиваются на две последовательности длиной N/4, причём для каждой их пары подбираются соответствующие весовые коэффициенты. Если является степенью числа 2, то последовательное прореживание входных значений может быть продолжено до получения двухточечных преобразований.

Данный алгоритм получил название БПФ с прореживанием по времени. Базовая операция его, называемая «бабочкой» (баттерфляй), состоит в получении выходных чисел P и Q из выходных A и B в соответствии с выражением

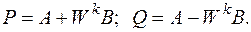(13.11)

Граф базовой операции изображён на рис. 13.3,в. Очевидно, что значения, получаемые в результате выполнения базовой операции, могут быть хранимы в запоминающем устройстве на месте исходных операндов, что существенно сокращает требуемый объём запоминающих устройств. Алгоритм БПФ, в котором реализуется такая переадресация данных, получил название алгоритма с замещением.

Второй распространённой формой алгоритма БПФ является метод прореживания по частоте, суть которого заключается в выполнении ДПФ от вспомогательных подпоследовательносте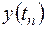й и 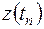половинной длины, получаемых из исходной в соответствии с выражением:

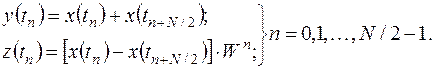(13.12)

Базовая операция БПФ с прореживанием по частоте имеет вид:

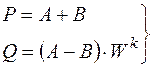(13.13)

и может быть представлена графом, изображённым на рис. 13.3,г.

Легко заметить сходство между алгоритмами БПФ с прореживанием по времени и по частоте. В обоих случаях при выполнении ДПФ требуется равное количество операций, и в том, и в другом случае вычисления могут быть проведены с замещением, иногда совпадают даже конфигурации графов преобразования, хотя значения весовых коэффициентов различны. Ещё одно общее свойство обоих видов алгоритма заключается в необходимости перестановки следования входных либо выходных отсчётов преобразования, выполняемое обычно с помощью двоичной инверсии их номеров. Потребность в такой перестановке вытекает из самой структуры алгоритмов. Действительно, при прореживании по времени для получения выходной последовательности в естественном порядке на выходе устройства необходимо выполнить перестановку данных таким образом, чтобы первым наступал нулевой отсчёт, вторым – (N-1)/2-й и т.д. В алгоритме прореживания по частоте аналогичная перестановка производится с выходными отсчётами.

Важной особенностью алгоритма БПФ является возможность использования его и для вычисления обратного дискретного преобразования Фурье (ОДПФ) [4,5], которое определяется выражением (13.7). Выполнив комплексное сопряжение последнего и разделив его на N, получим

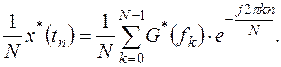(13.14)

Правая часть формулы (13.14) представляет собой ДПФ последовательности 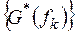и может быть вычислена с использованием алгоритма БПФ. Тогда искомую последовательность 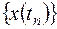можно получить, взяв комплексно-сопряжённое с (13.14) выражение и умножив его на N:

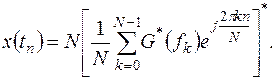(13.15)

На практике здесь обычно используется перестановка всех, кроме 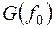, членов последовательности 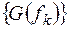таким образом, что 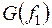меняется местами 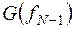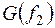с ; - с 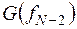и т.д.

Существуют различные алгоритмы БПФ [3], однако все они могут быть получены путём последовательного применения одной операции – представления одномерного массива двумерным [5]. При этом если число членов входной последовательности преобразования N является простым, т.е. не разложимым на произведения меньших целых чисел, то одномерный сигнал 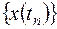невозможно представить в виде двумерного массива, поэтому для такого сигнала не существует алгоритма БПФ. Для выхода из этого положения в большинстве практических задач исходную последовательность удлиняют путём дополнения её нулями до желаемого числа членов, являющегося составной величиной, после чего становится возможным выполнение преобразования с фиксированным или смешанным основанием. Кроме того, в последнее время разработан также ряд специальных быстрых алгоритмов вычисления ДПФ на основе вспомогательных преобразований, с использованием цифровых фильтров, на базе представления ДПФ в виде ЦС [3], позволяющих выполнять преобразования для различных размерностей массивов входных данных, в том числе и для простых N.

С вычислением выражений вида свёртки, как указано выше, связана также широкая область цифровой обработки сигналов, например, цифровая фильтрация, под которой подразумевается выделение с использованием цифровых методов полезного сигнала на фоне флюктуирующих шумов в определённом диапазоне частотного спектра [10].

Математически работа цифрового фильтра ЦФ во временной области описывается разностным уравнением (уравнением в конечных разностях)

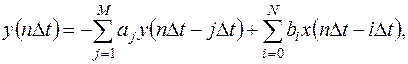(13.16)

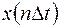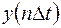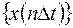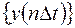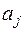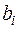где и - n-е отсчёты входного и выходного сигналов фильтра; коэффициенты и представляют собой константы ЦФ с постоянными параметрами, или отсчёты решётчатых функций, зависящих от n или других показателей (ЦФ с переменными параметрами).

Цифровые фильтры принято делить на два класса: нерекурсивные и рекурсивные [18]. Если в выражении (13.16) все коэффициенты 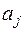равны нулю, то фильтр, реализующий этот алгоритм, называется нерекурсивным и алгоритм его работы записывается как

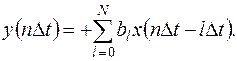(13.17)

Если в (13.16) хотя бы один из коэффициентов 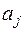не равен нулю, то такой фильтр называется рекурсивным. Очевидно, что нерекурсивный цифровой фильтр (НРЦФ) представляет собой устройство без обратной связи, а рекурсивный ЦФ (РЦФ) – устройство с обратной связью. В отдельных случаях выделяют также в виде отдельных классов полурекурсивные, адаптивные и прогнозирующие ЦФ [10].

Возможна и другая классификация цифровых фильтров: ЦФ с конечными (КИХ-фильтры) и с бесконечными (БИХ-фильтры) импульсными характеристиками [5,13]. При этом любой реальный нерекурсивный ЦФ является КИХ-системой, а рекурсивный фильтр представляет собой, как правило, БИХ-систему. Однако возможны варианты НРЦФ, являющиеся системами с импульсными характеристиками конечной длины [18].

Структурная реализация ЦФ может иметь различный вид. Весьма широкое распространение получила каскадная форма представления фильтров, элементами которой являются биквадратные звенья [4]. Функционирование последних описывается рекуррентными соотношениями второго порядка

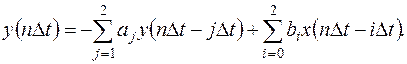(13.18)

Структурная схема возможной реализации биквадратного блока представлена на рис 13.3,д.

Широкому распространению биквадратного звена в цифровой фильтрации служит не только факт относительно более низкой (в данном случае) чувствительности характеристик ЦФ к погрешности задания коэффициентов (связанных с физическими и стоимостными ограничениями на разрядность), но и гибкость в построении различных по сложности структур фильтров, возможность широкого использования эффективных методов распараллеливания, временного разделения и поточной обработки.

В заключении необходимо отметить, что представленные фрагменты теории цифровой обработки сигналов, естественно, не охватывают всего многообразия задач, методов и алгоритмов этой области науки. Данный материал по сути дела является лишь введением в некоторые разделы ЦОС, в котором с целью упрощения изложения сознательно опущен или лишь упомянут ряд существенных положений цифровой обработки. В то же время с уверенностью можно утверждать, что представленные здесь фундаментальные структуры (цифровая свёртка, быстрое преобразование Фурье и рекуррентное соотношение второго порядка) лежат в основе разнообразных алгоритмов ЦОС и именно для реализации их необходимо в первую очередь создавать эффективные специализированные микропроцессорные интегральные средства.

Лекция №8

ВЕЙВЛЕТ ПРЕОБРАЗОВАНИЕ