Лекция № 7.
Все реальные непрерывные сигналы являются плавными функциями времени. Скачки значений в них практически не наблюдаются. Поэтому такие сигналы можно представить последовательностью их значений, взятых с некоторым шагом по времени. Значение сигнала в фиксированный момент называется отсчетом.
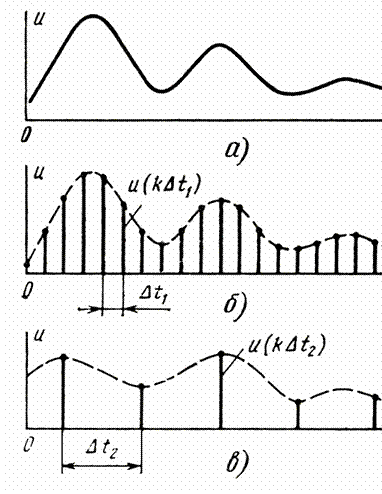
На этом рисунке показан непрерывный сигнал и его отсчеты с различным шагом по времени. При малом шаге (рис. б) последовательность отсчетов достаточно точно описывает сигнал, а при большом шаге (рис. в) по отсчетам нельзя восстановит форму сигнала, так как пропущены его характерные экстремальные точки.
Как же часто следует брать отсчеты, чтобы по ним можно было полностью восстановить сигнал?
Ответ на этот вопрос дает теорема, доказанная в 1933 г. Советским ученым академиком В.А.Котельниковым. и названная его именем.
Согласно этой теореме любой непрерывный сигнал 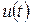 с конечным спектром (имеющим максимальное значение
с конечным спектром (имеющим максимальное значение 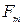 ) можно представить в виде дискретных отсчетов
) можно представить в виде дискретных отсчетов 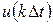 , частота дискретизации которых должна быть выбрана не менее чем в два раза выше максимального значения спектра сигнала:
, частота дискретизации которых должна быть выбрана не менее чем в два раза выше максимального значения спектра сигнала: , передать его по линии связи, а затем восстановить исходный аналоговый сигнал.
, передать его по линии связи, а затем восстановить исходный аналоговый сигнал.
Теорема Котельникова является основой для дискретизации непрерывных сигналов по времени, так как, во – первых, доказывает, что непрерывный сигнал можно заменить его дискретными значениями, во – вторых, дает правило вычисления шага дискретизации – 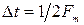 . При таком шаге дискретизации ряд Котельникова дает точное временное представление сложного сигнала.
. При таком шаге дискретизации ряд Котельникова дает точное временное представление сложного сигнала.
Физический смысл теоремы Котельникова.
Теорема Котельникова утверждает, что если требуется передать непрерывный сигнал 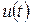 с ограниченным спектром по каналу связи, то можно не передавать все его значения: достаточно лишь передать его мгновенные значения (отсчеты) через интервал
с ограниченным спектром по каналу связи, то можно не передавать все его значения: достаточно лишь передать его мгновенные значения (отсчеты) через интервал 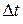 . Поскольку сигнал
. Поскольку сигнал 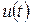 полностью определяется этими значениями, то по ним он может быть восстановлен на приемном конце системы связи. Для этого достаточно соединить отсчеты плавной кривой. Это можно объяснить тем, что сигнал
полностью определяется этими значениями, то по ним он может быть восстановлен на приемном конце системы связи. Для этого достаточно соединить отсчеты плавной кривой. Это можно объяснить тем, что сигнал 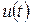 между отсчетами может изменяться только плавно, так как частоты выше
между отсчетами может изменяться только плавно, так как частоты выше 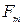 дающие быстрые изменения, в сигнале отсутствуют. Ведь отсчеты берутся достаточно часто, и тем чаще, чем выше максимальная частота
дающие быстрые изменения, в сигнале отсутствуют. Ведь отсчеты берутся достаточно часто, и тем чаще, чем выше максимальная частота 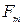 .
.
Практическое применение теоремы Котельникова.
Дискретизация сигнала осуществляется достаточно просто: периодически на короткое время через интервал 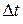 ключом замыкается цепь от источника сигнала
ключом замыкается цепь от источника сигнала 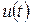 к нагрузке – получаем отсчеты
к нагрузке – получаем отсчеты 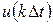 . Далее эти отсчеты, пройдя через канал связи, поступают на вход идеального фильтра нижних частот (ФНЧ) с верхней частотой пропускания
. Далее эти отсчеты, пройдя через канал связи, поступают на вход идеального фильтра нижних частот (ФНЧ) с верхней частотой пропускания 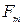 . На выходе фильтра получается исходный непрерывный сигнал
. На выходе фильтра получается исходный непрерывный сигнал 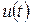 .
.

Структурная схема системы связи с использованием теоремы Котельникова.
На передающей стороне берутся отсчеты 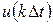 сигнала
сигнала 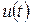 в моменты
в моменты 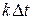 . Далее отсчеты любым способом передаются по каналу связи. Идеальный ФНЧ на приемном конце восстанавливает исходный сигнал
. Далее отсчеты любым способом передаются по каналу связи. Идеальный ФНЧ на приемном конце восстанавливает исходный сигнал 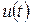 .
.
Частота следования импульсов, называемая также частотой дискретизации, определяется по теореме Котельникова:
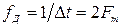 .
.
Например, частота дискретизации для речевого (телефонного) сигнала, имеющего максимальное значение спектра сигнала  , будет равна
, будет равна 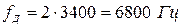 . Согласно рекомендациям МККТТ
. Согласно рекомендациям МККТТ 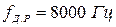 и, соответственно,
и, соответственно, 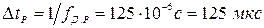 .
.
Теорема Котельникова в многоканальной электросвязи.
Возможность передачи вместо непрерывных сигналов последовательности импульсов (отсчетов) позволяет осуществить временное разделение каналов. Дело в том, что при импульсной передаче период следования импульсов обычно намного больше их длительности, то есть импульсы имеют большую скважность – при большой скважности между импульсами одного сигнала остается промежуток, на котором можно разместить импульсы от других сигналов. Этот способ и называется временным разделением. В настоящее время уже реализованы многоканальные системы передачи с временным разделением каналов на 12, 15, 30, 120, 480, 1920 речевых сигналов.
 2014-02-02
2014-02-02 44438
44438
