Модели ARIMA

В эконометрике анализ временных рядов с использованием оценки спектральной плотности (спектральный анализ) играет, как правило, вспомогательную роль, помогая установить периоды характерных циклов. Наибольшее распространение получили параметрические модели стационарных случайных процессов — модели авторегрессии и скользящего среднего.

Пусть X_t — значения стационарного случайного процесса, m =EX_t, x_t=X_t- m. Введем случайный процесс x(t) Î N (0,s ²), для которого E x _t= 0, D x _t= s ², E x _t x _t+t= 0 (t¹0). Случайный процесс x_t будем называть белым шумом.

Модель AR (1) авторегрессии первого порядка имеет вид

x_t= a x_{t- 1}+ξ _t, (12.1)

где |a|< 1 — необходимое условие стационарности процесса x_t. В случае a= 1 получаем модель случайного блуждания

x_t=x_{t- 1}+ξ _t. (12.2)

Временной ряд (12.2) является нестационарным. Пусть x₀= 0. Тогда

Ex_t= 0, Dx_t= s ²t,

а для стационарного процесса дисперсия не должна зависеть от времени t. Допустим, что для модели (12.1) дисперсия постоянна: Dx_t= s _x². Тогда из формулы (12.1) следует, что

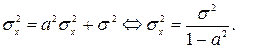(12.3)

Наши вычисления показывают, что действительно, процесс авторегрессии первого порядка стационарен только при условии |a|< 1. При этом надо дополнительно потребовать, чтобы начальное значение x₀ было случайной величиной, причем Ex₀= 0, Dx₀= s _x².

Если же исходить из фиксированного (неслучайного) значения x₀= 0, то можно показать, что значение дисперсии (12.3) устанавливается в пределе при t ®∞.

Модель AR (2) авторегрессии второго порядка определяется формулой

x_t=a₁x_t-1+ a₂x_t-2+ξ_t. (12.4)

Условие стационарности в этом случае сводится к требованию, чтобы корни (в общем случае комплексные) уравнения

1 - a₁z^{- 1} - a₂z^{- 2}=0 (12.5)

удовлетворяли условию |z|< 1.

Уравнение (12.5) получается из (12.4) заменой x_t на 1, x_{t- 1} на z^-1, x_{t- 2} на z^-2 и ξ _t на 0.

Это же правило можно использовать и в случае AR (1), получается уравнение 1 -az^{- 1} = 0, решение которого z=a удовлетворяет условию |z|< 1.

Модель AR (p) авторегрессии p -го порядка определяется формулой

x_t=a₁x_t-1+ a₂x_t-2+…+ a_px_t-p+ξ_t. (12.6)

и определяет стационарный временной ряд при условии, что корни уравнения

1- a₁z^-1 - a₂z^-2-…- a_pz^-p= 0 удовлетворяют условию |z|< 1.

Модель MA (1) скользящего среднего (Moving average) первого порядка имеет вид x_t= ξ _t+b ξ _t-1 и определяет стационарный временной ряд при любых значениях параметра b. Аналогично определяется модель MA (q) скользящего среднего q -го порядка:

x_t=ξ_t+b₁ξ_t-1+…+ b _qξ_t-q. (12.7)

Обобщая определения (12.6) и (12.7), введем модель авторегрессии-скользящего среднего ARMA (p,q):

x_t= a₁x_t-1+ …+ a_px_t-p +ξ_t+b₁ξ_t-1+…+ b _qξ_t-q, (12.8)

числа p и q определяют порядок модели ARMA (p,q).

При изучении нестационарных временных рядов используется более общая модель ARIMA (m,d,n) — модель авторегрессии — проинтегрированного скользящего среднего, в русской аббревиатуре — АРПСС. По сравнению с ранее обсуждавшимися моделями модель ARIMA предполагает d – кратное применение оператора конечных разностей

x_t = y_t - y_t-1 (12.9)

к исходному временному ряду.

Однократное применение операции (12.9) устраняет линейный тренд. Действительно, если y_t=а+bt, то y_t-1=а+b (t- 1) и x_t=b. Повторяя эту операцию несколько раз, можно получить (с некоторым приближением) стационарный временной ряд, который описывает модель ARMA. При восстановлении исходного ряда производится суммирование его членов, что соответствует интегрированию в непрерывном времени. Последнее обстоятельство проясняет смысл названия модели ARIMA.